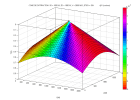
Front d'onde issu d'un point diffractant en x_d = z_d = 1000 m au temps t = 0, se propageant dans le plan x,z à la vitesse de propagation constante V = 2000 m/s, déployé dans l'espace-temps x,z,t.
Le plan x,z en t = 0 est la structure du sous-sol (ici un seul point diffractant).
L'enregistrement est fait dans le plan x,t en z = 0 (hyperbole de diffraction).

Le front d'onde circulaire issu de x_d,z_d à t = 0 trace le cône de diffraction dans le volume x,z,t.
L'intersection du cône avec un plan à t constant donne le cercle de rayon Vt.
Au temps t = 0.5s = z_d/V, le front d'onde atteint la surface z = 0 en x_d = 1000 m (sommet de l'hyperbole de diffraction pour l'incidence verticale).
Puis le front d'onde balaye l'axe x selon l'hyperbole t_d = (1/V)(z_m²+(x-x_m)²)^½

La vitesse apparente horizontale pour une incidence θ par rapport à la verticale est V_ax = V/sinθ.
La pente de l'hyperbole de diffraction au point d'émergence du rayon d'incidence θ est dt/dx = 1/V_ax = sinθ/V.
Les couleurs sur la surface du cône de diffraction correspondent aux valeurs de dt/dx pour les différentes valeurs de θ : cyan pour l'incidence verticale (dt/dx = 0) à rouge pour les grands angles d'incidence (dt/dx tend vers 1/V, pente de l'asymptote à l'hyperbole).

La figure illustre le concept de base utilisé dans la migration des coupes de sismique réflexion :