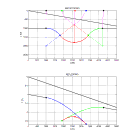
Réflexion sur un synclinal quand V = V(x,z)

Haut :
Interface plane de pendage α = 10° entre une couche de vitesse V₀ = 500 m/s et V₁ = 1000 m/s causant une variation latérale de vitesse pour les rayons réfléchis sur une interface sous-jacente en forme de synclinal.
Le synclinal comporte des segments de réflecteurs horizontaux (noir) et des segments en forme d'arcs de cercle ayant leurs centres en-dessous (segments bleu et vert) et en-dessus (segment rouge) du réflecteur. Les rayons réfléchis en provenance du segment rouge se croisent sur le centre de l'arc de cercle correspondant.
La loi de Snell pour la transmission à travers l'interface pentée s'écrit par rapport à la normale à l'interface qui fait un angle de α = 10° par rapport à la verticale. Les rayons partant à la verticale du synclinal font l'angle α avec la normale à l'interface pentée, se transmettent en faisant l'angle β avec cette normale tel que sinβ/V₀ = sinα/V₁, soit β = 5°, et émergent en surface avec un angle α-β = 5° par rapport à la verticale.

Bas :
Réflexions provenant des interfaces ci-dessus.
Pour la réflexion sur l'interface plane, dt/dx = sin(10)/V₀ = .35 10^-3 s/m.
Pour la réflexion sur les segments horizontaux noirs du synclinal, dt/dx = sin(α-β)/V₀ = .17 10^-3 s/m : la variation latérale de vitesse produit une pente apparente sur un reflecteur horizontal.
La triplication n'est plus symétrique comme lorque la vitesse ne dépend que de la profondeur.
Le point d'émergence du rayon rouge partant à la verticale du fond du synclinal (rond rouge) est décalé latéralement et le temps correspondant sur la triplication n'est pas le temps minimum.
Le temps minimum correspond au rayon qui arrive perpendiculairement à la surface, appelé le rayon image. En applicant la loi de Snell sur l'interface plane, son angle d'incidence par rapport à la verticale dans le milieu de vitesse V₁ est γ-α où sin(γ)/V₁ = sin(α)/V₀.