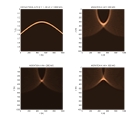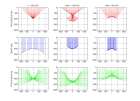
Point diffractant migré avec Vmig ≠ V
1ère colonne :
Haut : rayons issus d'un point diffractant en xd = 0, zd = 1000 m, sous des angles d'incidence θ entre 0 et 45°
Milieu : hyperbole de diffraction pour V = 1000 m/s : t = zd/cosθ/V et dt/dx = sinθ/V sur l'hyperbole
Bas : migration par superposition de demi-cercles à Vmig = 1000 m/s : les demi-cercles de rayons r = Vmigt = Vt passent par le point diffractant
2ème colonne : hyperbole de diffraction migrée avec Vmig > V
Haut : rayons migrés avec rm > r et θm > θ (rm = Vmigt , sinθm/Vmig = sinθ/V) :
les points rouges sont les positions migrées en profondeur, trop profondes et mal focalisées avec une courbure vers le haut.
(zm = rmcosθm et xm = x-rmsinθm).
Milieu : migration temps (l'axe des temps est le temps migré tm = zm/Vmig),
toujours mal focalisée mais sans décalage en temps pour θ ≈ 0.
Bas : les demi-cercles de rayon rm ne se croisent pas. Leur enveloppe commune correspondant à la position migrée (celle des points rouges ci-dessus).
3ème colonne : hyperbole de diffraction migrée avec Vmig < V
Haut : rayons migrés avec rm < r et θm < θ.
Les points rouges sont les positions migrées en profondeur, pas assez profondes et mal focalisées avec une courbure vers le bas.
Milieu : migration temps (l'axe des temps est le temps migré tm = zm/Vmig),
toujours mal focalisée mais sans décalage en temps pour θ ≈ 0.
Bas : les demi-cercles de rayon rm ne se croisent pas. Leur enveloppe commune correspondant à la position migrée (celle des points rouges ci-dessus).
On explique ainsi les images obtenues avec la migration d'une hyperbole par superposition de demi-cercles avec Vmig > V et Vmig < V :