Examen 2002
On se propose d’adapter la migration « phase-shift » à des coupes sismiques à déport constant.
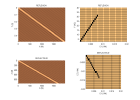
Rappeler comment la migration « phase-shift » à déport nul permet d’obtenir p(x,z) à partir de p(x,t, h=0) pour une vitesse de propagation V(z) par prolongement vers le bas du champ d’onde décomposé en ondes planes.
Soit un volume de données sismiques p(s,g,t) résultant d’une acquisition 2D le long d’un axe Ox.
Les abscisses mesurées le long de l’axe du profil sont notées s pour les sources S, g pour les géophones G, y=(s+g)/2 pour les points-milieux Y. Le demi-déport est h=(g-s)/2.
Faire le diagramme permettant de passer des coordonnées (s,g) aux coordonnées (y,h) et indiquer où on trouve les collections de traces correspondant à un point de tir commun, un récepteur commun, un point-milieu commun, une coupe à déport constant.
Etablir l’expression du temps de trajet pour une réflexion sur un réflecteur de pendage α et une vitesse constante V en fonction de s,g,α puis en fonction de y,h,α
(utiliser le triangle OGS’ où O est l’intersection du réflecteur avec la surface et S’ est la source virtuelle).
Pour réaliser la migration de p(s,g,t), il faut prolonger p(s en z=0, g en z=0, t) le champ d’onde vers le bas successivement
pour les géophones p(s en z=0, g en z=Dz, t) puis pour les sources p(s en z=Dz, g en z=Dz, t) :
Pour une collection en point de tir commun p(s0,g,t), le prolongement vers le bas des géophones peut se faire par « phase-shift »
avec kzg = -(ω/V)(1-kg2V2/ω2)½.
Donner l’expression de kg en fonction de l’angle θ entre S’S et S’G et α.
Indiquer les étapes de calcul (TF, prolongement, TF-1) permettant de passer de p(s0 en z = 0, g en z = 0, t) à p(s0 en z = 0, g en z = Dz, t) avec kzg .
Que faut-il faire pour passer de p(s en z=0, g en z=0, t) à p(s en z=0, g en z=Dz, t) pour l’ensemble des données ?
Pour une collection en récepteur commun p(s,g0,t), le prolongement vers le bas des sources peut se faire
avec kzs = -(ω/V)(1-ks2V2/ω2)½.
Indiquer les étapes de calcul permettant de passer de p(s en z = 0 , g0 en z = Dz, , t) à p(s en z = Dz, g0 en z = Dz, , t) avec kzs .
Que faut-il faire pour passer de p(s en z=0, g en z=Dz, t) à p(s en z=Dz, g en z=Dz, t) pour l’ensemble des données ?
Le passage de p(s en z=0, g en z=0, t) à p(s en z=Dz, g en z=Dz, t) peut se faire directement avec kzgs = (kzg + kzs) .
Indiquer les étapes de calcul nécessaires pour passer de p(s en z = 0, g en z = 0, t) à p(s en z = Dz, g en Dz, t) en faisant le prolongement vers le bas avec kzgs .
La longueur limitée L du dispositif d’enregistrement pose un problème pour les opérations précédentes : lequel et quel est son effet ?
Pour éviter ce problème, on va désormais travailler avec p(y,h,t) .
Montrer que ks = (ky-kh)/2 et kg = (ky+kh)/2 en exprimant les dérivées partielles de p par rapport à s et g en fonction de celles par rapport à y et h et en utilisant les relations entre (s , g) et (y , h).
Exprimer kzgs en fonction de ky et kh pour obtenir kzyh(ky , kh) .
Vérifier que pour kh=0, kzyh se réduit à l’opérateur de prolongement vers le bas de la migration « phase-shift » à déport nul.
Indiquer les étapes de calcul nécessaires pour passer de p(y,h,z=0,t) à p(y,h,z=Dz,t) en faisant le prolongement vers le bas avec kzyh .
La ligne de la coupe migrée à la profondeur Dz correspond à p(y,h=0,z=Dz,t=0).
Cette condition remplace le principe des réflecteurs explosant pour la migration à déport non nul.
Expliquer ce que signifie cette condition en considérant un rayon réfléchi pour un couple S,G au cours du prolongement vers le bas.
Exprimer la coupe migrée P(ky,Dz) en fonction de P(ky,kh,z=0,ω).
Si on ne migre qu’une seule coupe de demi-déport h0 , P(kh) = exp(-ikhh0)p(h0) .
Montrer que l’intégrant de l’intégrale sur kh dans l’expression de la migration se met sous la forme
exp (iφ(kh)) où φ(kh) = kzyhz-khh0 .
Le point stationnaire de φ(kh) correspond au rayon réfléchi pour le déport h0 .
En supposant que α = 0, donner l’expression de kh0 en fonction de z et h0.
En déduire l’expression de exp(iφ(kh0) ), approximation à l’ordre 0 de l’intégrale sur kh .
Toujours dans l’hypothèse où α=0, donner l’expression de φ(kh0) en fonction du temps de trajet de la réflexion.
Pour aller plus loin : Alkhalifah, T., 2000, Prestack phase-shift migration of separate offsets
Contrôle continu 2002
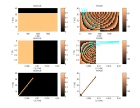
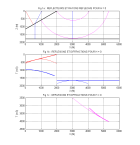
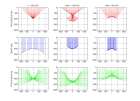
I - La figure montre une section sismique à déport nul à la limite entre un
dôme de sel et des sédiments stratifiés subhorizontalement.
La vitesse apparente des réflexions pentées provenant du flanc du dôme est de 1440 m/s.
La TF2D de la section montre que ces réflexions sont aliasées pour des fréquences supérieures à 20 Hz.
(les figures proviennent de Biondi B., 2001, Kirchhoff imaging beyond aliasing).
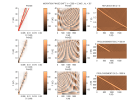
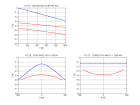
Expliquer ce qu’on observe sur la TF2D.
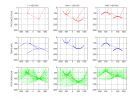
Souligner sur la section sismique une réflexion de type A et déterminer la valeur maximum de la vitesse de propagation
dans les sédiments en supposant qu’elle est constante.
Déterminer l’intervalle Δx entre traces en utilisant les valeurs données.
Dessiner la TF2D qui aurait été obtenue avec un intervalle Δx/2 (faire le dessin sous la TF2D représentée sur la figure, en respectant l’échelle).
Quelle est la bande de fréquence utilisable pour migrer la section sans aliasing si on utilise les pentes inférieures
ou égales à celles de A dans la migration ?
Jusqu’à quelle fréquence peut-on monter pour la migration des réflexions subhorizontales ?
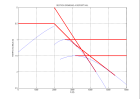
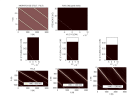
Rappeler comment on calcule kx en fonction de l’indice n de la trace (1≤n≤N).
Expliquer comment on passe du plan (kx-ω) au plan (kx-kx) dans la migration de Stolt.
La section ne contenant aucune réflexion de pente opposée à celle de A, la partie aliasée du plan (kx-ω)
représente les vraies valeurs de P(kx-ω) pour kx > kxN .
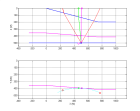
Proposer une modification de l’algorithme de Stolt
permettant de migrer les pentes de même signe que A pour kx tel que 0≤kx≤2kxN .
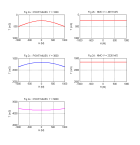
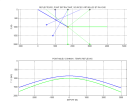
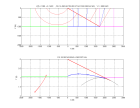
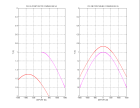
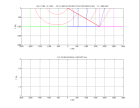
Voici le résultat
à comparer à celui obtenu sans modification pour une somme d'ondes planes harmoniques avec aliasing.
 -
-
 -
-


 -
-