JMM ex EOST : Ondes - Imagerie sismique

Sismique réflexion : Introduction - Dispositifs d'acquisition, coordonnées et collections d'enregistrements
Migration à V constante et déport nul : Points diffractants - Réflecteurs plans - TF - Echantillonnage - Stolt - Kirchhoff
Migration à V constante et déport non nul : Point de tir - DMO
Migration à V(z) et déport nul : Relation temps-profondeur - Rayons et "phase-shift"
Migration à V(x,y,z) et déport nul : Faibles variations latérales - Equation iconale - Equations paraxiales - Différences finies 15 - Renversement temporel
Migration à déport non-nul : Equations de prolongement - Imagerie et d termination de la vitesse - R fraction
Transformation : τ-p - S paration montante-descendante
Documents : Figures et programmes - Sujets exams - Livres et liens

Les vid os du cours s'ouvrent en cliquant sur les titres de paragraphe.
Les figures grand format s'ouvrent toutes dans la même fenêtre en cliquant sur les icônes.
Les animations Java s'ouvrent en cliquant sur les liens en gras.
Les programmes Matlab écrits pour réaliser les figures sont accessibles en cliquant sur le nom du programme (prog.m).

Introduction

L'imagerie sismique du sous-sol par sismique réflexion à partir de la surface utilise les ondes réfléchies pour déterminer la géométrie des interfaces géologiques avec une bonne résolution latérale. On réalise une série d'expériences où les échos provoqués par une source ponctuelle sont enregistrés sur de nombreux récepteurs échantillonnant une distance (ou surface pour la 3D) limitée. Le traitement des données pour obtenir une image du sous-sol comporte plusieurs étapes . Un préalable indispensable est de pouvoir déceler et séparer les échos de faible amplitude en provenance de la profondeur parmi l'ensemble des ondes enregistrées. L'imagerie n'utilise que les réflexions primaires ayant effectué un trajet direct source-réflecteur-récepteur. Si l'on réussit à les isoler, la question suivante est : d'où proviennent les échos? Transformer les temps de parcours des ondes réfléchies en une image des réflecteurs en profondeur est le but premier de l'étape du traitement sismique appelée migration. On donne ici les bases essentiellement géométriques des différentes méthodes de migration pour un milieu de propagation acoustique. On ignore dans un premier temps les aspects concernant la préservation des amplitudes. On suppose aussi que la vitesse de propagation V est connue.

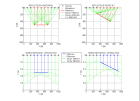
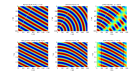
Les différences entre la structure du sous-sol en profondeur et l'image sismique obtenue en juxtaposant les enregistrements en temps faits par des couples source-récepteur confondus sont illustrées sur les figures suivantes (les temps correspondent aux temps aller-retour dits temps doubles).

- -
l gende isis - isis.m

Pour un segment de réflecteur plan horizontal, une conversion de l'axe des temps en profondeur suffit à ramener la réflexion à la position du réflecteur. Cependant, les extrémités du réflecteur se comportent comme des point diffractants qui renvoient l'onde incidente dans toutes les directions. Les hyperboles de diffraction doivent tre focalisées sur les points diffractants par la migration.
Pour un segment de réflecteur plan penté, il y a un décalage latéral du au trajet oblique des rayons réfléchis alors que la réflexion est imagée en temps à la verticale des couples source-récepteur. L'extension latérale de la réflexion est plus grande que celle du réflecteur. De plus, la pente apparente en temps est différente du pendage du réflecteur.
Pour un réflecteur courbé (ici un arc de cercle), une forme concave focalise les rayons réfléchis. La réflexion résultante est donc d'extension latérale plus restreinte que le réflecteur. Au contraire, une forme convexe défocalise les rayons réfléchis. La réflexion résultante est donc d'extension latérale plus grande que le réflecteur.
Lorsque la courbure d'un réflecteur concave est telle que le foyer co ncide avec la surface, l'image en temps est focalisée en un point. Si le foyer est situé sous la surface, la courbure de la réflexion est inverse de celle du réflecteur. De plus, l'image est inversée, les points de réflexion situés sur la droite du réflecteur étant imagés sur la gauche de la réflexion.
Sur toutes ces figures, on observe que l'hyperbole de diffraction est tangente à la réflexion pour le couple source-récepteur pour lequel le rayon réfléchi co ncide avec un rayon diffracté issu du point de réflexion. Cette propriété est à la base des méthodes de migration qui reconstruisent la structure du sous-sol comme un ensemble de points diffractants.

Des expériences utilisant la propagation d'ondes à la surface de l'eau permettent de se familiariser avec les notions utilisées. Versez de l'eau dans un plat en verre de forme rectangulaire et munissez-vous d'une baguette et de deux peignes à dents très espacées.

Plonger l'extrémité de la baguette dans l'eau et observer l'onde circulaire émise (et les réflexions sur les bords, un problème que l'on a aussi avec les simulations numériques et avec la Terre).
Plonger le peigne dans l'eau (un réflecteur explosant) et observer l'onde plane émise (et les ondes circulaires émises par les extrémités du peigne) : le principe de Huygens en action.
Faire varier l'orientation du peigne et observer la variation de vitesse apparente de l'onde plane sur les bords.
Plonger l'extrémité de la baguette dans l'eau (un point diffractant), la maintenir fixe, puis plonger le peigne source au voisinage d'un bord : observer l'onde circulaire diffractée par la baguette.
Plonger un peigne dans l'eau parallèlement à un bord (un réflecteur plan horizontal), le maintenir fixe, puis plonger l'autre peigne au voisinage du bord : observer l'onde plane réfléchie.
Plonger un peigne dans l'eau avec une orientation quelconque (un réflecteur plan penté), le maintenir fixe, puis plonger l'autre peigne au voisinage du bord : observer l'onde plane réfléchie.

Observer les vagues la surface des lacs ou de la mer est aussi tr s instructif : voir par exemple cette vid o.

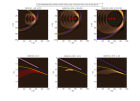
Un point diffractant (point rouge) met une onde diffract e sph rique lorsqu'il est atteint par le front d'onde sph rique mis par une source situ e en surface (point bleu). Sur les figures suivantes, les fronts d'onde et les enregistrements faits en surface sont repr sent s au temps o :
- l'onde directe atteint le point diffractant
- le front d'onde diffract atteint la surface (point vert)
- le front d'onde diffract atteint le r cepteur x = 900m (point vert).

$diffraction$ - $diffraction$ -

Inversement la r tropropagation du front d'onde diffract fait converger le front d'onde sur la position du point diffractant au temps o il a t mis. On obtient ainsi l'image du point partir de l'onde qu'il a mise. L'imagerie sismique est bas e sur ce ph nom ne, appel migration.

- -

Les interf rences entre les ondes diffract es issues de points diffractants proches sont constructives sur la r flexion provenant du r flecteur form par la juxtaposition des points diffractants.

$diffraction-r flexion$ - sdr.m

Strobbia C., 2016, An introduction to seismic migration without a single equation

Dispositifs d'acquisition, coordonnées et collections d'enregistrements

Le dispositif d'acquisition des donn es est constitu d'un ensemble de r cepteurs (g ophones enregistrant la vitesse de d placement du sol terre, hydrophones enregistrant la variation de pression en mer) dispos s en ligne le long d'un profil (cas 2D) ou en lignes parall les le long d'un andain (cas 3D). Un enregistrement l mentaire, fait par un groupe de r cepteurs connect s pour fournir un seul signal lectrique, est appel une trace. Chaque tir est enregistr par plusieurs centaines de traces. La collection d'enregistrements r sultant d'un m me tir est dite collection de traces en tir commun.
En mer, un bateau tire un cable d'enregistrement de plusieurs kilom tres de long (plusieurs cables parall les en sismique 3D) permettant l'enregistrement simultan s de centaines de traces s par es par un intervalle de l'ordre de la dizaine de m tres. La source est une impulsion de pression g n r e par un r seau de canons air (voir par exemple cette vid o et cet article).
A terre, on proc de de la m me fa on, mais le dispositif r cepteur peut tre dispos de fa on sym trique par rapport la source, souvent constitu e de camions vibrateurs (voir par exemple cette vid o).

Les donn es sont acquises selon le principe de la couverture multiple, afin que chaque point de r flexion soit illumin selon un ventail d'angles d'incidence. La source est actionn e de fa on ce que l'intervalle entre tirs Δs soit un multiple de l'intervalle entre traces Δg. Ainsi, les points milieux g om triques des couples sources-r cepteurs chantillonnent le profil avec un intervalle Δy = min(Δs , Δg)/2 r gulier. Le tri des traces en point-milieu commun permet de constituer des collections de traces ayant le m me point-milieu et des d ports sources-r cepteurs variant entre les distances source-r cepteur minimum et maximum. Dans un milieu homog ne ou stratifi interfaces horizontales, les r flexions sur une collection de traces en point-milieu commun ont des points de r flexion situ s la verticale du point-milieu. Le nombre de traces ayant un point-milieu commun est l'ordre de couverture.

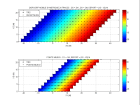
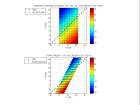
Le recouvrement des positions de tir et de r cepteurs le long d'un profil rend n cessaire une repr sentation en plan de la g om trie du dispositif d'acquisition o les axes correspondent respectivement aux abscisses des r cepteurs et des tirs le long du profil (coordonn es terrain) ou l'abscisse des points-milieux et au d port source-r cepteur (coordonn es utilis es pour le traitement). Voici des exemples de g om tries pour des dispositifs d'acquisition mobiles sym triques, dissym triques et fixes dans les coordonn es (r cepteurs, tirs) et (points-milieux , tirs), le d port source-r cepteur tant figur en couleur.

- - - sgyh.m

Sismique 2D : sources et récepteurs placés le long d'un profil, abscisse ou distance mesur e le long du profil sources
s = x_s récepteurs
g = x_r point milieu
y = (s+g)/2 demi-déport
h = (g-s)/2
collections ou sections avant sommation source commune
p(s₀,g,t) récepteur commun
p(s,g₀,t) point milieu commun
p(y₀,h,t) déport constant
p(y,h₀,t)
Exemples de donn es acquises lors de la campagne sismique EW0108 Gulf of Corinth Profil GOC11, effectu e en 2001 sous la responsabilit scientifique de Brian Taylor (University of Hawai'i).
Les donn es non trait es (points de tir) sont archiv es au Marine Geoscience Data System, Lamont-Doherty Earth Observatory of Columbia University. Les profils trait s (stacks et migrations) sont archiv s par Shipley, T., Gahagan, L., Johnson, K., and Davis, M., editors, 2005, Seismic Data Center, University of Texas Institute for Geophysics
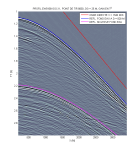
l gende ptgoc
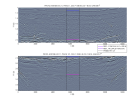
l gende tr1goc

Les r sultats scientifiques de la campagne sismique EW0108 Gulf of Corinth, destin e l'imagerie des s diments, du socle et des failles dans une zone d'extension active, sont d crits dans les publications suivantes :
Taylor, B.; Goodliffe, A.; Sachpazi, M.; Hirn, A.; EW0108 Science Party, 2001, First Results from EW0108 Marine Seismic Survey of the Gulf of Corinth, Eos Trans. AGU, 82(47), Fall Meet. Suppl.,
Zelt, B. C., Brian Taylor, B., Weiss, J. R., Goodliffe, A. M., Sachpazi, M., and Hirn, A., 2004, Streamer tomography velocity models for the Gulf of Corinth and Gulf of Itea, Greece, Geophysical Journal International, 159, p. 333 346
Taylor, B., Weiss, J.R., Goodliffe, A.M., Sachpazi, M., Laigle M. and Hirn A., 2011, The structures, stratigraphy and evolution of the Gulf of Corinth rift, Greece, Geophysical Journal International, 185, p. 1189 1219

Points diffractants explosants : cone de diffraction - migration

Une inhomogénéité localisée en M dans un milieu de vitesse constante V agit comme une source ponctuelle secondaire. Elle émet une onde sphérique au temps où elle est atteinte par l'onde incidente. Lorque le déport est nul, les trajets aller-retour SMR peuvent être remplacés par des trajets simples MR dans un milieu de vitesse moitié. Tout se passe comme si une source placée en M explosait à t=0. La migration consiste à concenter l'onde diffractée au point M au temps t=0 où elle a été émise. En répétant cette procédure pour chaque point du sous-sol, on obtient une image du plan (x,z).

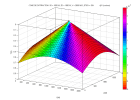
$cône de diffraction$
l gende cone - cone.m hyperbole de diffraction en z=0 position du point diffractant à t=0
V²t² = (x-x_m)²+(z-z_m)² t_d = (1/V)(z_m²+(x-x_m)²)^½ x = x_m , z = z_m
migration de p(x,t) par sommation des diffractions émises à t=0 par chacun des points du sous-sol sommation sur la courbe de diffraction image de M = onde(x_m,z_m,t=0)
algorithme de sommation sur trajectoire de diffraction dans le plan xt : ∀(x_m,z_m) S = ∑_xp(x,t_d(x,x_m,z_m)) p(x_m,z_m) = S

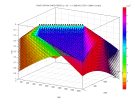
La sommation est constructive si :

M est effectivement un point diffractant (par exemple, l'extrémité d'un réflecteur sur une faille).
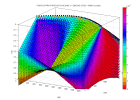
M est un point de réflexion. Le rayon normal au réflecteur de pendage θ est le rayon diffracté d'incidence θ. La contribution à S provient de la portion de la courbe de diffraction tangente à la réflexion. La pente commune est dt_d/dx = sinθ/V (inverse de la vitesse apparente horizontale). La méthode s'applique quelle que soit la géométrie du réflecteur, par exemple un synclinal, qui produit une réflexion présentant une triplication.

- -
l gende cones - cone.m

De façon quivalente la sommation sur les trajectoire de diffraction, chaque chantillon du plan (x,t,z=0) peut tre plac sur le r flecteur semi-circulaire dont il peut provenir dans le plan (x,z,t=0). La superposition des demi-cercles produit l'image migr e.

- -
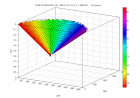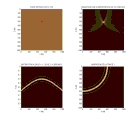l gende cone1 - l gende migsdc - migsdc.m r flecteur semi-circulaire à t=0 correspondant une impulsion en x = x₀ , t = t₀ z = 0
V²t² = (x-x_m)²+(z-z_m)² z_m = (V²t₀²-(x₀-x_m)²)^½
algorithme de superposition de 1/2 cercles dans le plan xz : ∀(x₀,t₀) ∀x_m : p(x_m,z_m) = p(x_m,z_m)+p(x₀,t₀)

Voici des exemples de migration de r flexions obtenues par la sommation de diffractions pour des points diffractants align s sur des segments de droite et sur un synclinal.
- -
l gende migsdc - migsdc.m

Voici la correspondance entre un r flecteur en forme de synclinal et la r flexion correspondante pour un milieu de vitesse constante V = 1000 m/s et des temps simples de propagation. Les segments courb s du synclinal sont des arcs de cercle.

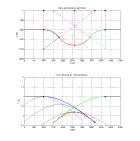
Le segment de courbe de diffraction qui contribue constructivement à la migration d'une réflexion correspond la zone de Fresnel dans laquelle l'interf rence entre une r flexion plane et une diffraction harmonique est constructive dans le plan (x,t,z=0). Sa largeur s'obtient en écrivant que le déphasage correspondant à la différence de longueur δl entre le trajet réfléchi et le trajet diffracté est inférieur à une demi-période (kδl < π). Soit x_F l'écart entre les points d'émergence en z=0 des rayons réfléchi et diffracté issus d'un m me point diffractant à la profondeur z_m et α l'angle sous lequel x_F est vu depuis la profondeur z_m :

-
l gende fresnel - fresnel.m tgα = x_F/z_m ≈ α δl ≈ x_Fsinα ≈ x_F²/z_m x_F² = πz_m/k = λz_m/2
tgα = x_Fcos²θ/z_m ≈ α δl ≈ x_Fcosθsinα ≈ x_F²cos³θ/z_m x_F² = πz_m/(kcos³θ)

Babcock, J. M. ; Harding, A. J. ; Kent, G. M. ; Orcutt, J. A. , 1998 An examination of along-axis variation of magma chamber width and crustal structure on the East Pacific Rise between 13 30'N and 12 20'N montrent l'effet des diffractions sur les rugosités de la croûte océanique sur les images sismiques à l'axe des dorsales.
Zhu, J., L. Lines and S. Gray, 1998, Smiles and frowns in migration/velocity analysis illustrent l'effet d'une mauvaise vitesse de migration. Voir aussi ce sujet d'examen et ces figures.

$point diffractant migré avec Vmig≠V$ -
l gende Vmig≠V - -
l gende Vmig≠V

Le traitement des donn es du profil EW0108-GOC11 fournit une coupe sismique par transformation des temps de trajet des r flexions primaires d port nul et sommation (stack) en point milieu commun le long du profil. On y observe simultan ment les r flexions visibles sur les points de tir et sur les coupes d port constant dans l'intervalle entre la r flexion primaire au fond de l'eau et les r flexions multiples dans l'eau : les r flexions dans la partie sup rieure des s diments syn-rift sont vues faible d port, celles dans la partie profonde (dont l'interface s diments syn-rift-socle) grand d port. Quelques pentes correspondant diff rents pendages de r flecteurs et diffractions associ es aux failles sont indiqu es sur la figure suivante. La conversion pendages-dt/dx est faite en utilisant la vitesse constante dans l'eau V = 1500 m/s. Comme la couche d'eau est paisse au centre du graben, cette approximation convient pour les s diments peu profonds. La migration la vitesse de l'eau fournit une image correcte faible profondeur, o l'on distingue clairement les blocs d coup s par les failles normales. Par contre la partie profonde est sous-migr e.

-
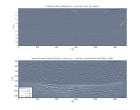
l gende goc11

Réflecteurs plans vibrants

La décomposition en points diffractants traite tous les pendages pour chacun des points du sous-sol. Une décomposition en ondes planes traite globalement chaque pendage.
Lorque le déport est nul, les trajets aller-retour des ondes réfléchies peuvent être remplacés par des trajets simples issus de sources placées sur les réflecteurs et explosant à t=0.
L'image en profondeur est donnée par le champ d'onde prolongé en profondeur au temps t=0.
L'utilisation d'ondes planes harmoniques permet d'obtenir les r flecteurs dans plan (x,z,t=0) partir de l'enregistrement dans le plan (x, z=0, t) en prolongeant le champ d'onde en profondeur par un simple déphasage.

. onde(x,z,t) enregistrement en z = 0 image à t = 0
plan d'onde t = xsin(α)/V + zcos(α)/V t = xsin(α)/V z = -xtg(α)/V
relation de dispersion k_x²+k_z² = ω²/V² k_x = ωsinθ/V k_z = -ω(1/V²-k_x²/ω²)^½
(- car onde montante)
onde harmonique = 1 pendage p(x,z,t) = Pe^{i(k_xx+k_zz-ωt)} p(x,t) = Pe^i(k_xx-ωt) p(x,z) = Pe^i(k_xx+k_zz)
superposition d'ondes harmoniques = tous pendages p(x,z,t) = ∫∫P(k_x,ω)e^{i(k_xx+k_zz-ωt)}dk_xdω p(x,t) = ∫∫P(k_x,ω)e^i(k_xx-ωt)dk_xdω p(x,z) = ∫∫P(k_x,ω)e^i(k_xx+k_zz)dk_xdω

Transformée de Fourier

Les facteurs constants, absorbés dans les gains appliqués pour la représentation des traces, sont omis.

TF inverse et directe dérivation translation convolution en x convolution en k p réel p réel symétrie dilatation
p(x) = ∫P(k_x)e^ik_xxdk_x p'(x) p(x-x₀) p∗q(x) = ∫p(ξ)q(x-ξ)dξ p(x)q(x) p(x) p(-x) P(x) p(ax)
P(k_x) = ∫p(x)e^-ik_xxdx = |P(k_x)|e^iχ(k_x) ik_xP(k_x) e^-ik_xx₀P(k_x) P(k_x)Q(k_x) P∗Q(k_x) P*(k_x) = P(-k_x) P*(k_x) p(-k_x) (1/|a|)P(k_x/a)

La TF détecte les périodicités : la TF de fonctions harmoniques est constituée d'impulsions aux nombres d'ondes correspondants. Une somme infinie d'harmoniques successives produit par interférence un peigne d'impulsions à la longueur d'onde fondamentale.

p(x) e^ik₀x 1 cosk₀x sink₀x ∑e^ink₀x ∑^∞e^ink₀x = ↑λ₀↑
P(k_x) δ(k_x-k₀) δ(k_x) δ(k_x-k₀)+δ(k_x+k₀) -i(δ(k_x-k₀)-δ(k_x+k₀)) ∑δ(k_x-nk₀) ∑^∞δ(k_x-nk₀) = ↑k₀↑

Voici quelques transformées intervenant en sismique

mesure sur [-a,a] autocorrélation signe(k_x) échelon
p(x)Π[-a,a] ∫p(x')p(x+x')dx' = p(x)∗p(-x) i/x H(x) = (1+signe(x))/2
P(k_x)∗(2/k_x)sin(k_xa) P(k_x)P*(k_x) = |P(k_x)|² signe(k_x) δ(k_x)+1/(ik_x)

La décomposition d'une onde sphérique en ondes planes harmoniques s'obtient explicitement par le calcul des composantes P(k_x,k_y) dans le plan z=0 puis par prolongement de chaque composante en z>0.

r² = x²+y²+z² k² = ω²/V² = k_x²+k_y²+k_z² e^ikr/r = ∫∫P(k_x,k_y)e^ik_zze^i(k_xx+k_yy)dk_xdk_y = ∫∫(i/k_z)e^ik_zze^i(k_xx+k_yy)dk_xdk_y
r² = x²+y² , x = rcosθ κ² = k_x²+k_y² , k_x = κcosη P(k_x,k_y) = ∫∫e^ikr/re^{-i(k_xx+k_yy)}dxdy = ∫∫e^ikre^{-iκrcos(θ-η)}drdθ
0≤r<∞ , -π≤θ≤π k_z réel donc κ/k<1 P(k_x,k_y) = ∫dθ∫e^{i(k-κcos(θ-η))r}dr = (i/k)∫dθ/(1-(κ/k)cos(θ-η)) = 2iπ/(k²-κ²)^½ = 2iπ/k_z
a = κ/k , t = tg(α/2) ∫dα/(1-acosα) = 2∫d(tgα/2)/((1-a)+(1+a)tg²α/2) = 2/(1-a)∫dt/(1+((1+a)/(1-a))t²) = 2/(1-a²)^½Arctg(((1+a)/(1-a))^½t) = 2π/(1-a²)^½

Echantillonnage : J F o u r i e r - JFourierJFourier - J u e F r r o i

La TF échantillonnée utilise un nombre fini d'harmoniques pour représenter le spectre. La longueur d'onde fondamentale correspond à la longueur d'enregistrement X, celle de l'harmonique la plus élevée à 2 fois le pas d'échantillonnage Δx (nombre d'onde de Nyquist k_xN = π/Δx). Si des longueurs d'onde plus petites sont présentes, la périodisation associée à l'échantillonnage superpose k_x = k_xN+2nπ/X avec k_x = -k_xN+2nπ/X (repliement spectral ou aliasing).

onde sur intervalle X périodisation en x → échantillonnage en k échantillonnage en x → périodisation en k longueurs et nombres onde
p(x) p∗↑X↑ p∗↑X↑.↑Δx↑ λ_x = ∞,X,X/2,..,2Δx
P(k_x) P.↑2π/X↑ P.↑2π/X↑∗↑2π/Δx↑ ±k_x = 0,2π/X,4π/X,..,π/Δx

Voici l'illustration de la TF échantillonnée pour des harmoniques complexes et réelles et des diracs réels :

- -
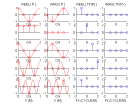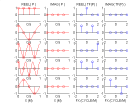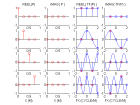
proptf.m

et de l'effet de l'aliasing spatial dans les plans (x,t) et (kx,ω) pour une r flexion harmonique :

l gende aliasing - alias.m

Biondi B., 2001, Kirchhoff imaging beyond aliasing illustre l'effet de l'aliasing sur les images et les opérateurs de migration.

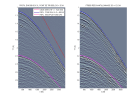
Le module de la TF2D d'un point de tir du profil EW0108-GOC11 montre que les arriv es la vitesse de l'eau (1520 m/s) sont alias es aux fr quences sup rieures 30 Hz pour un pas d' chantillonnage Δg = 25 m. Il est possible de d aliaser partiellement l'enregistrement en reconstituant le plan f-k correspondant un chantillonnage spatial deux fois plus dense Δg = 12.5 m, compte-tenu de la dissym trie de l'enregistrement.

- -
l gende ptfk

Migration de Stolt

En effectuant un changement de variable dans le domaine de Fourier, on remplace le calcul d'une intégrale double par celui d'une TF2D inverse.
Le changement de variable implique une interpolation des valeurs complexes de P (source d'artefacts) ainsi qu'une pondération des amplitudes en cosθ (optionnelle).
A cause de la périodisation, la section migrée inclut les symétriques des portions de réflecteurs migrés au-dela des limites latérales du domaine de calcul, ce qui provoque des artefacts de migration.
De plus, le prolongement vers le bas de l'onde montante depuis la surface z=0 jusqu'à la profondeur z est équivalent au prolongement vers le haut de l'onde descendante depuis le bas de la section z=Z jusqu'à la profondeur z. La réponse impulsionnelle comporte donc deux demi-cercles tangents centrés respectivement en z=0 (réflecteur) et z=Z (artefact).

TF2D chgt. variable → interpolation (+ pondération) image à t = 0 par TF2D inverse
P(k_x,ω) = ∫∫p(x,t)e^-i(k_xx-ωt)dxdt ω = -Vk_z(1+k_x²/k_z²)^½
P(k_x,k_z) = P(k_x,ω(k_x,k_z))
dω/dk_z = A(k_x,k_z) = Vcosθ p(x,z) = ∫∫(AP)(k_x,k_z)e^i(k_xx+k_zz)dk_xdk_z
e^-ik_z(Z-z) = e^{-i(j2pi/Z)(Z-z)} = e^{i(-j2π+k_zz)} = e^ik_zz

Voici l'illustration des étapes de la migration de Stolt p(x,t) → P(k_x,ω) → P(k_x,k_z) → p(x,z) pour :

- - - l gende stoltop - stolt.m
une onde plane monochromatique , une somme d'harmoniques pour un pendage fixé (k_x/ω = cte) sans et avec aliasing spatial

- - - l gende stoltimp - stolt.m
une impulsion en (x=0 , t=0.25s) , en (x=0 , t=1s) , au centre de la section.

Voici ce qui se passe si on migre une même section avec différentes vitesses de migration (voir ce sujet d'examen)

Stolt, R.H., 1978, Migration by Fourier transform
Garcia, D., L. le Tarnec, S.Muth, E. Montagnon, J. Por e, and G. Cloutier, 2013, Stolt s f-k Migration for Plane Wave Ultrasound Imaging

Migration de Kirchhoff

La migration dans le domaine de Fourier manipule les ondes planes conformément à l'équation des ondes. Une intégrale de Fourier représente une sommation de sinusoïdes qui n'est constructive qu'au voisinage des points stationnaires de l'argument de l'exponentielle complexe. La méthode de la phase stationnaire est basée sur cette propriété (pour une onde, la phase est stationnaire dans la direction de propagation). On passe ainsi de l'expression de la migration dans le domaine de Fourier à celle de la migration par sommation selon les hyperboles de diffraction. Des termes correctifs affectant la phase et l'amplitude apparaissent lorsqu'on fait un développement à l'ordre 2 : ils sont pris en compte dans la migration de Kirchhoff.

calcul de I = ∫e^iφ(k)dk par développement de φ(k) autour de k₀ tel que φ'(k₀) = 0 ordre 0 : φ(k) ≈ φ(k₀)
I ≈ e^iφ(k₀) ordre 2 : φ(k) ≈ φ(k₀)+((k-k₀)²/2)φ''(k₀)
I ≈ e^iφ(k₀)∫e^{i((k-k₀)²/2)φ''(k₀)}dk = e^iφ(k₀)(2π/|φ''(k₀)|)^½e^{sign_φ''(k₀)iπ/4}
p(x_m,z_m) = ∫∫P(k_x,ω)e^{i(k_xx_m+k_z(k_x,ω)z_m)}dk_xdω = ∫dx∫P(x,ω)dω∫e^iφ(k_x)dk_x
φ(k_x) = -k_x(x-x_m)+k_z(k_x)z_m
r_d(x) = ((x-x_m)²+z_m²)^½ , t_d(x) = r_d(x)/V , tgθ_d = (x-x_m)/z_m
k_x0 = ωsinθ_d/V , k_z(k_x0) = -ωcosθ_d/V , φ(k_x0) = -ωt_d(x)
e^iφ(k_x0) = e^-iωt_d(x)
p(x_m,z_m) = ∫dx∫e^-iωt_dP(x,ω)dω = ∫p(x,t_d(x))dx = sommation de p sur hyperbole de diffraction
φ''(k_x) = k_z''(k_x)z_m = z_mV/|ω|(1-k_x²V²/ω²)^-3/2
φ''(k_x0) = V(z_m/cos³θ_d)/|ω| = V(r_d/cos²θ_d)/|ω|
∫e^iφ(k_x)dk_x = V^-½cosθ_dr_d^-½e^iπ/4|ω|^½e^-iωt_d(x)
p(x_m,z_m) = V^-½∫dxcosθ_dr_d^-½∫dωe^iπ/4|ω|^½e^-iωt_d(x)P(x,ω)

La formule de Green fournit directement l'expression de la migration de Kirchhoff en 3D. La solution élémentaire G(x,x_m) de l'équation des ondes pour une source impulsionnelle δ(x-x_m) placée en x_m est l'onde sphérique issue de x_m et enregistrée à la surface en x. Le champ d'onde réfléchi P(x) se propage selon l'équation des ondes homogène. La formule de Green permet d'exprimer P(x_m) en fonction de l'intégrale de surface de P(x,y,z=0) et (∂/∂z)P(x,y,z=0). A cause de la surface libre en z=0, la solution élémentaire est la différence entre les ondes sphériques provenant de la source impulsionnelle en z>0 et virtuelle en z<0. Elle s'annule en z=0, ce qui permet d'exprimer P(x_m) uniquement en fonction de P(x,y,z=0), seul enregistré, et gradG (l'angle entre gradG et l'axe vertical est l'angle de diffraction θ_d). Pour la migration, il faut rétropropager l'onde de x à x_m le long du cône de diffraction en remontant dans le temps de t_d à t=0 (par un déphasage de -ωt_d). On trouve que la quantité à sommer le long de l'hyperboloïde de diffraction est ∂P/∂t avec un terme de pondération en amplitude.

ΔP+k²P(x,ω) = 0
ΔG+k²G(x,x_m,ω) = δ(x-x_m)
r_d = |x-x_m| = Vt_d , e_{r_d} = (x-x_m)/r_d
G(x,x_m,ω) = -e^ikr_d/r_d
gradG(x,x_m,ω) = e_{r_d}-(ik-1/r_d)e^ikr_d/r_d
gradG(x,x_m,ω) ≈ -ike_{r_d}e^ikr_d/r_d pour kr_d >> 1 ∫∫∫P(x,ω)δ(x-x_m)dx = ∫∫∫(PΔG-GΔP)dx = ∫∫∫div(PgradG-GgradP)dx
P(x_m,ω) = ∫∫(PgradG-GgradP)(x,y,z=0,ω).dS
G(x,x_m,ω) = -e^ikr_d(z_m)/r_d(z_m)+e^ikr_d(-z_m)/r_d(-z_m)
P(x_m,ω) = ∫∫(PgradG)(x,y,z=0,ω).dS = -2∫∫ikP(x,y,z=0,ω)e^ikr_dcosθ_d/r_ddxdy
p(x_m, t=0) = (2/V)∫∫dxdycosθ_d/r_d∫-iωP(x,y,z=0,ω)e^-iωt_ddω
p(x_m, t=0) = (2/V)∫∫(∂/∂t)P(x,y,z=0,t_d)cosθ_d/r_ddxdy

Schneider, W.A., 1978, Integral formulation for migration in two and three dimensions.

Migration par point de tir

A d port non-nul, les points diffractants dans le plan (x,z) sont atteints par l'onde issue de la source au temps direct source-point diffractant t_sd. Le temps d'arriv e en z = 0 est la somme de ce temps et du temps diffract depuis le point diffractant. La migration peut tre faite par sommation des amplitudes diffract es le long de cette trajectoire de diffraction.
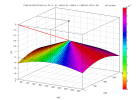
Pour un couple source-r cepteur, la surface dans le plan (x,z) correspondant un temps t est une demi-ellipse (une ellipse est engendr e avec une corde de longueur constante fix e en deux points). Un chantillon au temps t peut donc tre plac le long de cette demi-ellipse. En superposant les demi-ellipses correspondant aux diff rents chantillons, on r alise la migration.

$cône de diffraction$ - cone.m hyperbole de diffraction en z=0 position du point diffractant à t = t_sd
temps direct source-point diffractant : t_sd = (1/V)((x_m-x_s)²+z_m²)^½ t_d = t_sd + (1/V)((x-x_m)²+z_m²)^½ x = x_m , z = z_m
migration de p(x,t) par sommation des diffractions émises par chacun des points du sous-sol au temps t_sd sommation sur la courbe de diffraction image de M = onde(x_m,z_m,t_sd)
algorithme de sommation sur trajectoire de diffraction dans le plan xt : ∀(x_m,z_m) S = ∑_xp(x,t_d(x,x_s,x_m,z_m)) p(x_m,z_m) = S

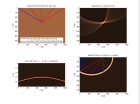
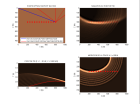
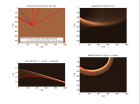
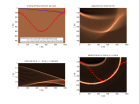
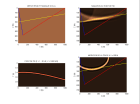
Voici un exemple de migration d'un point de tir pour un point diffractant, des points diffractants align s sur un segment de droite et un synclinal et pour un r flecteur pent :

$migration point de tir - point diffractant$ - - - - - migsdc.m

Dip Move-Out

Pour un réflecteur plan horizontal, les temps de réflexion t enregistrés avec un déport non nul sont ramenés à déport nul par une correction dynamique (NMO) t→t_n. Pour un r flecteur plan de pendage α, l'hyperbole de r flexion observ e sur un point de tir est d cal e la verticale de la source virtuelle. Sa courbure et ses asymptotes correspondent la vitesse de propagation V du milieu.
Sur un point milieu commun, l'hyperbole de r flexion est centr e sur la valeur de d port nulle mais sa courbure et ses asymptotes sont fonction de V/cosα. Dans le triangle source virtuelle S_v - point d'intersection O du r flecteur avec la surface - r cepteur G, on a :

(S_vG)² = (OS_v)²+(OG)²-2(OS_v)(OG)cos(2α) (Vt)² = s²+g²-2sgcos(2α) point milieu fix y₀ , t₀ = 2y₀sinα/V
s = y-h ; g = y+h (Vt)² = (y-h)²+(y+h)²-2(y²-h²)(cos²α-sin²α) = 4y²sin²α+4h²cos²α t² = (4y₀²sin²α+4h²cos²α)/V² = t₀²+4h²cos²α/V²

Voici des exemples de trajectoires de r flexion en point de tir, points milieux et d port nul pour un milieu comportant un r flecteur pent et un r flecteur horizontal se croisant en un point :
- -

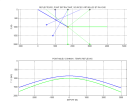
Les points de r flexion sur un r flecteur pent pour un point milieu commun ne sont pas confondus comme dans le cas o le pendage est nul. Pour s'affranchir de ce ph nom ne il faut effectuer une migration partielle appel e Dip Move Out (DMO). Si on ne fait pas d'hypothèse sur le pendage, une impulsion sur une section à déport constant h correspond à un réflecteur elliptique dont les foyers sont la source et le récepteur. Les temps à déport nul t₀ correspondant aux différents pendages sont obtenus en construisant les rayons normaux au réflecteur elliptique. Ceux-ci intersectent l'axe z=0 en des points-milieux y₀ différents de celui de l'impulsion initiale. L'ellipse DMOest la courbe t₀(y₀) : en reportant l'amplitude de chaque échantillon de la section à déport constant le long de l' ellipse DMO associée et en sommant, on obtient la section temps à déport nul quelques soient les pendages.

ellipse de migration E pour une impulsion en y=0 à t intersection rayon normal à E avec z=0 longueur rayon normal entre point courant M de E et (y₀,0)
dmo.m
t_n² = t²-4h²/V² y_m²/t²+z_m²/t_n² = V²/4 y₀ = y_m(1-t_n²/t²) V²t₀²/4 = (y_m-y₀)²+z_m² t₀²/t_n²+y₀²/h²=1

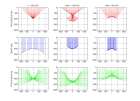
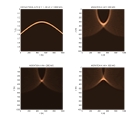
Voici des figures illustrant l'op rateur DMO t(t₀, x₀) pour un demi-d port h = 1000 m dans le cas o V = V0 = cte et dans le cas o V(z) = V0+az, en distinguant la partie de l'op rateur correspondant aux rayons r fl chis vers le haut et celle aux rayons r fl chis vers le bas (voir paragraphe suivant) :

- -
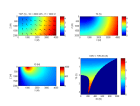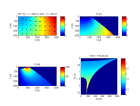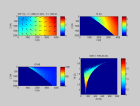
dmovz.m

Liner, C.L., 1999, Concepts of normal and dip moveout
Artley C. and D. Hale, 1994, Dip-moveout processing for depth-variable velocity
Black J.L., K.L. Schleicher and L. Zhang, 1993, True-amplitude imaging and dip moveout
Deregowski, S.M. and Rocca F., 1981, Geometrical optics and wave theory of constant offset sections in layered media: Geophys. Prosp., 29, 374-406.

Relation temps-profondeur pour V(z)

Quand la vitesse d pend de la profondeur, la relation temps de propagation verticale - profondeur n'est pas lin aire. De m me, la relation fr quence - longueur d'onde verticale d pend de la profondeur. L'analyse des temps de propagation des hyperboles de r flexion sur les points milieux fournit V_RMS(t). On en d duit V(t) par d rivation (formule de Dix). t(z) peut tre mesur directement si l'on dispose d'un puits, ce qui permet de "caler" en profondeur les r flexions au niveau du puits.

Par exemple, pour une augmentation lin aire de la vitesse avec la profondeur et une propagation verticale (θ = 0, k_x = 0, k_z = k), on a :

V(z) = V₀+az dt = dz/V(z)
ω = V(z)k_z(z) t(z) = ∫(dz/V(z)) = (1/a)Log(1+az/V₀) V_RMS²(z) = (1/t(z))∫(V(z)dz) = (z/t(z))(V₀+az/2) V(z) = d(t(z)V_RMS²(z))/dz
V(t) = V₀e^at z(t) = (V₀/a)(e^at-1) V_RMS²(t) = (1/t)∫(V²(t)dt) = (V₀²/(2at))((e^2at-1) V²(t) = d(tV_RMS²(t))/dt

Migration pour V(z) par tracé de rayons ou "phase-shift"

Quand la vitesse ne dépend que de la profondeur, la vitesse apparente horizontale le long d'un rayon est constante. Pour calculer les courbes de diffraction exactement, il faut tracer des rayons à partir de chaque profondeur en utilisant la loi de Snell. L'augmentation de la vitesse avec la profondeur est favorable pour l'imagerie des forts pendages. En effet, l'angle d'incidence diminuant vers la surface, le rayon concave parcourt une distance horizontale inférieure à celle dans un milieu de vitesse constante. Il est donc moins sensible aux variations latérales de vitesse. De plus, il est possible d'utiliser les rayons diffractés vers la bas pour imager les réflecteurs pentés par en dessous (par exemple les flancs des dômes de sel). Pour une faible ouverture angulaire, l' approximation V_RMS est utilisable.

-
l gende migvz - migvz.m

La loi de Snell s'exprime exactement dans le domaine de Fourier en exprimant k_z(k_x,ω,z) en fonction de V(z) : la migration par "phase-shift" est une méthode itérative en z basée sur cette propriété.

migration "phase-shift" k_z(jΔz) = -ω(1/V(jΔz)²-k_x²/ω²)^½ = -ωcosθ(jΔz)/V(jΔz)) P(k_x,ω,nΔz) = P(k_x,ω,z=0)∏_j(e^{iΔzk_z(jΔz)}) = P(k_x,ω,z=0)e^{iΔz∑_j(k_z(jΔz))}

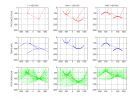
Voici l'illustration des étapes initiale, interm diaire et finale de la migration phase-shift pour une vitesse constante et une vitesse V(z) :

Pour mod liser une section sismique d port nul lorsque la vitesse d pend de la profondeur, on peut utiliser le m me principe. La TF du mod le p(x,z,t=0) donne P(k_x,z,t=0). On remonte vers la surface depuis la profondeur maximum par des d phasages successifs k_z(k_x,ω,z)Δz et en ajoutant chaque pas en profondeur la contribution de P(k_x,z,t=0) cette profondeur.

mod lisation "phase-shift" k_z(jΔz) = ω(1/V(jΔz)²-k_x²/ω²)^½ = ωcosθ(jΔz)/V(jΔz)) P(k_x,ω,z-Δz) = P(k_x,ω,z)e^iΔzk_z(z)+P(k_x,t=0,z-Δz)

Si la m thode phase-shift traite correctement la phase quand la vitesse d pend de la profondeur, elle ignore la variation d'amplitude li e la r fraction des rayons. La m thode WKBJ de r solution de l' quation d'onde pour V(z) donne l'effet sur l'amplitude.

∂²P/∂z²+k_z(k_x,ω,z)²P(k_x,ω,z) = 0 P(k_x,ω,z) = A(z)e^i∫k_z(z)dz 2k_zdA/dz+Adk_z/dz = 0 A(z)/A(z₀) = (k_z(z₀)/k_z(z) )^½

Voici la correspondance entre un r flecteur en forme de synclinal et la r flexion correspondante pour un milieu comportant une couche de vitesse V0 = 500 m/s sur un milieu de vitesse V1 = 1000 m/s et des temps simples de propagation. Les segments courb s du synclinal sont des arcs de cercle.

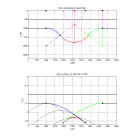
Gazdag, J., 1978, Wave equation migration with the phase-shift method
Hale D., N. R. Hill, and J. Stefani, 1992, Imaging salt with turning seismic waves montrent comment utiliser les ondes réfractées par un gradient de vitesse pour imager les réflecteurs par dessous.
Zhang, J. and McMechan, G. A., 1997, Turning wave migration by horizontal extrapolation montrent comment combiner prolongement vertical et horizontal du champ d'onde pour imager tous les pendages.
Margrave G.F., 2001, Direct Fourier migration for vertical velocity variations généralise la migration de Stolt au cas où V=V(z)

Migration pour V(x,y,z) par tracé du rayon image ou "phase-shift" avec correction

Si les variations latérales de vitesse sont petites par rapport aux variations avec la profondeur, on peut se contenter d'apporter des corrections aux méthodes précédentes.

Le temps minimum entre un point diffractant et la surface correspond au rayon image, orthogonal à la surface (puisque le front d'onde atteint en premier la surface selon une incidence nulle). Si on effectue une sommation sur trajectoire de diffraction hyperbolique (sans tenir compte des variations latérales de vitesse), la somme doit être placée en profondeur non pas à la verticale du point d'émergence du rayon image, mais le long du rayon image au temps correspondant au temps de l'apex de la trajectoire de diffraction. Ceci nécessite de tracer uniquement les rayons image.

Black J.L. and M. A. Brzostowski, 1994, Systematics of time-migration errors

On peut aussi utiliser la méthode de phase-shift avec une vitesse moyenne V_m(z) et effectuer une correction dans le domaine spatial tenant compte approximativement de l'écart V(x,z)-V_m(z). On fait un développement au premier ordre de k_z et on applique un déphasage vertical variant latéralement en plus du terme tenant compte de la propagation sous tous les angles à la vitesse moyenne.

migration "phase-shift" avec correction k_z ≈ -ω/V(x,z)+ω/V_m(z)-ω(1/V_m(z)²-k_x²/ω²)^½ p(x,z+Δz) = ∫dωe^{-iω(1/V(x,z)-1/V_m(z))Δz}{∫P(k_x,ω,z)e^{-iω(1/V_m(z)²-k_x²/ω²)^½Δz}e^ik_xxdk_x}

Voici la correspondance entre un r flecteur en forme de synclinal et la r flexion correspondante pour un milieu comportant une couche de vitesse V0 = 500 m/s sur un milieu de vitesse V1 = 1000 m/s et des temps simples de propagation. L'interface a un pendage de 10 . Les segments courb s du synclinal sont des arcs de cercle.

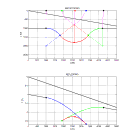
l gende syncliVxz

Opérateur de différences finies pour l'équation iconale

Si les trajectoires de diffraction sont trop déformées par les variations latérales de vitesse pour qu'une sommation sur une trajectoire hyperbolique soit constructive, il est nécessaire de les déterminer avant d'effectuer la sommation. Ceci nécessite de déterminer les temps de trajet à partir de chaque point diffractant. La résolution numérique de l'équation iconale par différences finies depuis chaque position source permet de déterminer les temps directs entre tout point de la surface et tous les points en profondeur.

équation iconale différences finies centrées opérateur pour Δx = Δz = a onde conique
(∂T/∂x)²+(∂T/∂z)² = 1/V(x,z)² (∂T/∂x) = (T(x+Δx,z)-T(x,z)+T(x+Δx,z+Δz)-T(x,z+Δz))/2Δx
(∂T/∂z) = (T(x,z+Δz)-T(x,z)+T(x+Δx,z+Δz)-T(x+Δx,z))/2Δz T(x+Δx,z+Δz) = T(x,z)+(2a²/V(x,z)²-(T(x+Δx,z)-T(x,z+Δz))²)^½ T(x+Δx,z+Δz) = min(T(x+Δx,z),T(x,z+Δz))+a/V(x,z)

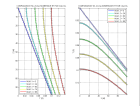
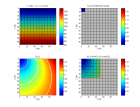
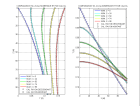
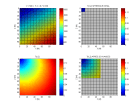
Voici des figures illustrant les temps calcul s par diff rences finies pour une source ponctuelle dans un milieu de vitesse constante ou gradient vertical et lat ral sans interface.

- - - - -
l gende iconal - iconal.m

Noble, M., A. Gesret and N. Belayouni, 2014, Accurate 3-D finite difference computation of traveltimes in strongly heterogeneous media
Mo L.W. and J. M. Harris, 2002, Finite-difference calculation of direct-arrival traveltimes using the eikonal equation

Equations d'onde paraxiales

Une autre façon de tenir compte des déformations des fronts d'onde par les variations de vitesse est d'utiliser une résolution numérique d'une équation d'ondes. On obtient des équations d'onde adaptées à la migration (propagation d'ondes montantes dans un domaine d'ouverture angulaire limité autour de l'incidence verticale : k_x ≈ 0 , k_z ≈ -ω/V) en faisant des développements limités de la relation de dispersion des ondes montantes valables pour des domaines restreints de pendage. Ces équations, obtenues dans le domaine de Fourier, peuvent être écrites dans le domaine spatial et temporel en identifiant les nombre d'ondes et pulsations avec des dérivées partielles. On obtient ainsi des équations d'onde paraxiales que l'on utilise pour prolonger le champ d'onde en profondeur par des méthodes de différences finies.

relation dispersion k_z = -ω(1/V²-k_x²/ω²)^½ terme de diffraction éq. paraxiale (x,z,ω) éq. paraxiale (x,z,t)
développement 15 k_z ≈ -ω/V(1-V²k_x²/2ω²) (ik_z)(-iω) = Vk_x²/2 ∂P/∂z = (V(x,z)/2iω)∂²P/∂x² ∂²p/∂z∂t = -(V(x,z)/2)∂²p/∂x²
développement 45 k_z ≈ -ω/V(1-(V²k_x²/ω²)/(2-V²k_x²/2ω²)) (ω²-V²k_x²/4)(ik_z) = (iω)Vk_x²/2 (ω²+(V²/4)∂²/∂x²)∂P/∂z = -(iωV/2)∂²P/∂x² (∂³/∂t²∂z-(V²/4)∂³/∂x²∂z)p = -(V/2)∂³p/∂t∂x²

Les relations de dispersion des équations paraxiales ne sont pas isotropes : la vitesse dépend de la direction de propagation. La réponse impulsionnelle de la migration n'est plus un demi-cercle. Pour le développement à 15 , c'est une ellipse. On le montre à partir de l'expression des composantes de la vitesse de groupe pour la relation de dispersion.

relation dispersion 15 phase stationnaire vitesse de groupe = grad(ω(k_x,k_z)) équation du front d'onde elliptique
k_z ≈ -ω/V(1-V²k_x²/2ω²) x = (∂ω/∂k_x)t
z = (∂ω/∂k_z)t ∂ω/∂k_x = (V²k_x/ω)/(1+V²k_x²/2ω²)
∂ω/∂k_z = -V/(1+V²k_x²/2ω²) x²/2+(z+Vt/2)² = V²t²/4

Ristow D. and T. Ruhl, 1994, Fourier finite-difference migration
Gray, S.H., J. Etgen, J. Dellinger and D. Whitmore, 2001, Seismic migration problems and solutions font une présentation générale des méthodes de migration et de leur utilisation pour l'estimation des vitesses.

Opérateurs de différences finies pour l'équation paraxiale à 15

Les opérateurs de différences finies de l'équation paraxiale à 15 s'obtiennent sous forme explicite ou implicite dans les différents domaines. La formulation explicite est instable. La formulation implicite, toujours stable, nécessite la résolution d'un système d'équations linéaires à matrice tridiagonale à chaque pas d'extrapolation (voir algorithme de Thomas). Dans le domaine (x,z,ω), on a :

coefficients des opérateurs de différences finies de l'équation paraxiale à 15 ∑a_iP_i = 0 analyse stabilité pour P = e^ik_xx
explicite (x,z,ω) P(x,z+Δz) = P(x,z)+(V/2iω)(Δz/Δx²)(P(x-Δx,z)-2P(x,z)+P(x+Δx,z)) P(z+Δz) = P(z)[1-4αsin²(k_xΔx/2)]
|P(z+Δz)| > |P(z)|
α = (V/2iω)(Δz/Δx²) P(x-Δx, ., ω) P(x, ., ω) P(x+Δx, ., ω)
P(., z, ω)
P(., z+Δz, ω) -α
0 2α-1
1 -α
0
implicite (x,z,ω) P(x,z+Δz) = P(x,z)+(V/2iω)(Δz/2Δx²)(P(x-Δx,z)-2P(x,z)+P(x+Δx,z)+P(x-Δx,z+Δz)-2P(x,z+Δz)+P(x+Δx,z+Δz)) P(z+Δz)[1+4αsin²(k_xΔx/2)] = P(z)[1-4αsin²(k_xΔx/2)]
|P(z+Δz)| = |P(z)|
α = (V/2iω)(Δz/2Δx²) P(x-Δx, ., ω) P(x, ., ω) P(x+Δx, ., ω)
P(., z, ω)
P(., z+Δz, ω) -α
-α 2α-1
2α+1 -α
-α

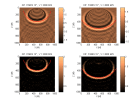
Voici des figures illustrant le r sultat de la migration par diff rences finies 15 (x, z, ω) implicite pour des r flecteurs plans de pendage croissants (la solution g om trique est donn e par la ligne rouge) et les r ponses impulsionnelles pour une vitesse constante V = 2000 m/s :

- -
l gende dif15 - dif15.m

L'opérateur implicite dans le domaine (x,z,t) comporte 2x2x3 = 12 termes. On l'obtient à partir de celui à 2x2 termes dans le domaine (k_x,z,t) en développant la dérivée seconde en x sur 3 termes.

implicite (k_x,z,t) P(z+Δz,t+Δt)-P(z+Δz,t)-P(z,t+Δt)+P(z,t) = (ΔtΔz/4)(Vk_x²/2)(P(z+Δz,t+Δt)+P(z+Δz,t)+P(z,t+Δt)+P(z,t))
α = (Vk_x²/2)(ΔtΔz/4) P(k_x, . , .)
P(k_x, z , t)
P(k_x, z , t+Δt)
P(k_x, z+Δz , t)
P(k_x, z+Δz , t+Δt) α-1
α+1
α+1
α-1
implicite (x,z,t)
α = -(V/2)(ΔtΔz/4Δx²) p(x-Δx, ., .) p(x, ., .) p(x+Δx, ., .)
p(., z , t)
p(., z , t+Δt)
p(., z+Δz , t)
p(., z+Δz , t+Δt) α
α
α
α -2α-1
-2α+1
-2α+1
-2α-1 α
α
α
α

Si on représente des enregistrements de sismique de puits p(z,t) en fonction de z et t' = t+z/V (temps dit réduit), on fait apparaitre les ondes montant verticalement à la vitesse V (dt/dz = -1/V) à temps constant (celui en z = 0). La longueur d'onde verticale des ondes montantes devient infinie (k'_z = 0) sans modifier la période. Ce changement de variable est aussi utile dans la résolution numérique de l'équation paraxiale : en temps retardé, le champ d'onde change peu avec Δz, et l'extrapolation vers le bas est facilitée. Pour une vitesse variable, on utilise la vitesse moyenne à la profondeur z , V_M(z).

temps réduit effet sur les pentes et sur les dérivées partielles k_z ≈ -ω/V , k'_z ≈ 0 éq. paraxiale 15
t' = t+z/V dt'/dz = dt/dz + 1/V
k'_z/ω = k_z/ω+1/V k'_z = k_z+ω/V k'_z = Vk_x²/2ω
t' = t+∫dz/V_M(z) P(z,t) = P'(z,t'(z,t))
∂P/∂z = ∂P'/∂z+(1/V_M(z))∂P'/∂t' , ∂P/∂t = ∂P'/∂t'
k_z = k'_z-ω/V_M(z) k'_z = k_z+ω/V_M(z) k'_z = -ω(1/V(x,z)-1/V_M(z))+Vk_x²/2ω

Pour éviter les réflexions parasites sur les limites latérales de la grille, il faut utiliser des conditions aux limites "anti-reflets". Dans le cas de la r solution de l' quation d'ondes 1D par diff rences finies, les r flexions peuvent tre supprim es en utilisant l' quation des ondes se propageant dans un seul sens sur les bords de la grille. Pour l' quation des ondes 2D, on peut utiliser des quations paraxiales pour les ondes allant vers les x croissants ou d croissants. Pour l' quation des ondes montantes, Clayton et Engquist (1980) ont propos une relation hyperbolique entre k_x/ω et k_z/ω approximant le quart de cercle de la relation de dispersion correspondant aux ondes allant vers les x croissants ou d croissants. Les 3 param tres a,b,c de cette relation sont obtenus en crivant l' galit des relations de dispersion pour 3 angles de propagation, par exemple θ = 30 , 60 et 90 .

eq. ondes vers gauche eq. ondes eq. ondes vers droite
1D (1/V)∂P/∂t = ∂P/∂x
-ω/V = k_x (1/V²)∂²P/∂t² = ∂²P/∂x²
(ω/V)² = k_x² (-1/V)∂P/∂t = ∂P/∂x
ω/V = k_x
2D k_x ≈ -ω/V(1-V²k_z²/2ω²) (ω/V)² = k_x²+k_z² k_x ≈ ω/V(1-V²k_z²/2ω²)
paraxiale Vk_z/ω = -(a-bVk_x/ω)/(1-cVk_x/ω)
cosθ_i = (a+bsinθ_i)/(1+csinθ_i) k_z = -ω/V(1-V²k_z²/ω²)^½ Vk_z/ω = -(a-bVk_x/ω)/(1-cVk_x/ω)
cosθ_i = (a-bsinθ_i)/(1-csinθ_i)

Clayton R.W. and B. Engquist , 1980, Absorbing boundary conditions for wave-equation migration

Une autre m thodes consiste entourer la grille avec des couches absorbantes sans contraste d'impédance avec le milieu de propagation. La méthode PML (Perfectly Matched Layer) introduit l'atténuation uniquement dans la direction perpendiculaire à l'interface. Le nombre d'onde dans la direction parallèle à l'interface n'est pas modifié. Il y a transmission totale dans la couche absorbante quelle que soit la période et l'incidence. L'atténuation est introduite par un changement de variable dans la couche. Pour une interface verticale en x = 0 séparant le mileu de propagation en x<0 d'un demi-espace absorbant en x>0, le calcul des coefficients de réflexion-transmission pour une onde plane SH montre qu'il y a bien transmission totale.

interface en x = 0 eq. paraxiale déplacement et contrainte continuité en x = 0
x < 0 x' = x k_z = Vk_x²/2ω u_y(x) = (e^ik_xx+Re^-ik_xx)e^ik_zz
σ_xy(x) = μik_x(e^ik_xx-Re^-ik_xx)e^ik_zz 1+R = T
(1-R) = T
R = 0 , T = 1
x > 0 x' = x(1+iα/ω) , α>0 k'_x = k_x/(1+iα/ω)
k_z = Vk'_x²/2ω u_y(x') = Te^ik_xx'e^ik_zz
σ_xy(x') = (μik_x/(1+iα/ω))Te^ik_xx'e^ik_zz

Collino, F, 1997, Perfectly matched absorbing layers for the paraxial equations
Pan, G., A. Abubakar, T. M. Habashy, (2012), An effective perfectly matched layer design for acoustic fourth-order frequency-domain finite-difference scheme

Renversement temporel

Le prolongement vers le bas du champ d'onde construit le cône de diffraction P(x,z,t) en reconstituant les hyperboles dans les plans P(x,z = iΔz,t) par le calcul de k_z ou ∂P/∂z. Alternativement, il peut tre construit en parcourant l'axe des temps en sens inverse pour reconstituer les fronts d'onde dans les plans P(x,z,t = T-iΔt), T tant le temps maximum d'enregistrement. Dans les deux cas, la pointe du cône (focalisation de l'onde diffract e) est atteinte en P(x,z,t=0).

ω/V = -k_z(1+k_x²/k_z²)½ 1/V∂P/∂t = ik_z(1+k_x²/k_z²)½P(k_x,k_z,t)

Baysal, E., D.D. Kosloff, and J. W. C. Sherwood , 1983, Reverse time migration

Robein E (2016). Reverse Time Migration: How Does It Work, When To Use It

Géométrie de réflexion et équations de prolongement à déport non-nul

Les op rateurs de prolongement vers la bas des champs d'onde enregistr s avec des sources et r cepteurs distincts (d port non nul) peuvent s'obtenir en consid rant la g ometrie de r flexion sur un r flecteur pent .

coordonnées sources - récepteurs coordonnées points-milieux - déports
θ_s = θ-α θ_g = θ+α y = (s+g)/2 h = (g-s)/2
∂t/∂s = -sinθ_s/V ∂t/∂g = sinθ_g/V ∂t/∂y = ∂t/∂s+∂t/∂g = 2sinαcosθ/V ∂t/∂h = -∂t/∂s+∂t/∂g = 2cosαsinθ/V
∂t/∂z_s = -cosθ_s/V = -(1-(V∂t/∂s)²)^½/V ∂t/∂z_g = -cosθ_g/V = -(1-(V∂t/∂g)²)^½/V ∂y/∂z = -1/tgα ∂h/∂z = -1/tgθ
∂t/∂z = ∂t/∂z_s+∂t/∂z_g = -2cosαcosθ/V = -((1-(V∂t/∂s)²)^½+(1-(V∂t/∂g)²)^½)/V ∂t/∂z = -((1-(V(∂t/∂y-∂t/∂h)/2)²)^½+(1-(V(∂t/∂y+∂t/∂h)/2)²)^½)/V
k_z/ω = -((1-(Vk_s/ω)²)^½+(1-(Vk_g/ω)²)^½)/V k_z/ω = -((1-(V(k_y-k_h)/2ω)²)^½+(1-(V(k_y+k_h)/2ω)²)^½)/V
∂P/∂z = (-iω/V)((1-(Vk_s/ω)²)^½+(1-(Vk_g/ω)²)^½)P(k_s,k_g,z,ω) ∂P/∂z = (-iω/V)((1-(V(k_y-k_h)/2ω)²)^½+(1-(V(k_y+k_h)/2ω)²)^½)P(k_y,k_h,z,ω)
∂P/∂z = (( (-iω/V(s))²-∂²/∂s²)^½+( (-iω/V(g))²-∂²/∂g²)^½)P(s,g,z,ω)

Imagerie d port non-nul et d termination de la vitesse par migration avant-sommation

L'image d'un point du sous-sol est obtenue en faisant le rapport dans le domaine fr quentiel entre les ondes montantes M (le champ d'onde r fl chi enregistr au r cepteur) et les ondes descendantes D (le champ d'onde mis par les sources) apr s prolongation vers le bas de ces champs, ce qui fournit le coefficient de r flexion R(x,z,ω). Dans le domaine temporel, cela correspond une d convolution du champ montant par le champ descendant (comme en sismique de puits). La d convolution tant potentiellement instable, on la remplace en pratique par la corr lation entre les champs montant et descendant, l'effet sur la phase tant identique. L'image I(x,z) d'un point peut tre obtenue avec diff rentes formules en sommant sur les fr quences et les positions de sources et en stabilisant les divisions par l'illumination et un ajout de bruit blanc.

d convolution d convolution stabilis e corr lation corr lation normalis e par l'illumination
R(x,z,ω) M(x,z,ω)/D(x,z,ω) M(x,z,ω)D*(x,z,ω)/(D(x,z,ω)D*(x,z,ω)) M(x,z,ω)D*(x,z,ω)
I(x,z) ∑_s∑_ω(M(x,z,s,ω)/D(x,z,s,ω)) ∑_s∑_ω(M(x,z,s,ω)D*(x,z,s,ω))/(D(x,z,s,ω)D*(x,z,s,ω)+ε²)) ∑_s∑_ωM(x,z,s,ω)D*(x,z,s,ω) ∑_s(∑_ω(M(x,z,s,ω)D*(x,z,s,ω))/∑_ω(D(x,z,s,ω)D*(x,z,s,ω)))

Voici l'exemple de la corr lation entre une onde harmonique sph rique mise par une source ponctuelle en surface (onde descendante) avec l'onde sph rique mise par la source virtuelle correspondant un r flecteur plan (onde r fl chie montante r tropropag e). Le r flecteur (ligne blanche) co ncide avec un maximum de la corr lation : temps source-r flecteur = temps source virtuelle -r flecteur. Les autres maximums de corr lation correspondent la p riodicit de l'onde harmonique : phases gales modulo 2π.

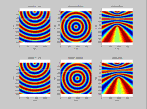
Voici l'exemple de la corr lation dans le cas des ondes planes.

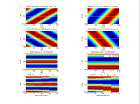
Lorque l'on effectue la migration avec la vraie vitesse de propagation V₀, le r flecteur est positionn la bonne profondeur d₀ pour tous les angles d'incidence.
Lorsqu'on utilise une vitesse de migration V_m fausse, les maximums de corr lations pour les diff rents angles d'incidence sont aux profondeurs z_m telles que k_z(V₀)d₀ = k_z(V_m)z_m .
En effet l'onde incidente propag e la vitesse V_m est e^{i(-k_z(V₀)d₀+ k_z(V_m)z_m)} . L'onde r fl chie r tropropag e la vitesse V_m est Re^{i(k_z(V₀)d₀-k_z(V_m)z_m)} . Le maximum de la corr lation Re^{-2i(k_z(V₀)d₀- k_z(V_m)z_m)} correspond la relation ci-dessus.
La d termination des profondeurs z_m pour diff rents angles d'incidence permet de trouver la vraie vitesse de propagation V₀ et la profondeur d₀.
Pour un angle d'incidence correspondant au param tre p_a la relation k_z(V₀)d₀ = k_z(V_m)z_m s' crit : (1/V₀²-p_a²)d₀² = (1/V_m²-p_a²)z_m² .
En liminant d₀ pour deux valeurs p_a et p_b du param tre donnant des maximums de corr lation en z_a et z_b, on obtient : V₀² = [z_a²(1/V_m²-p_a²)-z_b²(1/V_m²-p_b²)]/ [z_a²(1/V_m²-p_a²)p_b²-z_b²(1/V_m²-p_b²)p_a²]

Schleicher, J., J. C. Costa, and A. Novais, 2008, A comparison of imaging conditions for wave-equation shot-profile migration

Imagerie d'un r fracteur par les ondes coniques

La migration peut tre adapt e au cas de l'onde conique le long d'un r fracteur de pendage α entre deux milieux de vitesse V₁ et V₂ (sinθ_c = V₁/V₂). Le lieu des points tels que la somme du temps d'arriv e de l'onde transmise en x_m le long du r fracteur et du temps diffract depuis les points d'abscisse x_m vers la surface soit constante pour une position de r cepteur x_g correspond la position migr e pour ce temps et cette trace. Le front d'onde transmis tant orthogonal au r fracteur, le temps d'arriv e sur un plan perpendiculaire au r fracteur est constant. Si le pendage est faible, ce plan peut tre assimil au plan vertical. d tant la distance source-r fracteur, on a :

temps d'arriv e en x_m le long du r fracteur temps diffract depuis le r fracteur migration par superposition de fronts d'onde
t₀ = d/cosθ_c/V₁+(x_m-dsin(θ_c-α)/cosθ_c)/cosα/V₂ t_d = ((x_g-x_m)²+z_m²)^½/V₁ p(x_m, z_m) = p(x_m, z_m)+p(x, (t₀+t_d)(x, x_m, z_m))

- migrefr.m

La m thode "plus-minus" peut tre impl ment e sans pointer les temps d'arriv e par la combinaison d'une convolution (addition des temps de trajet) et d'une corr lation (soustraction des temps de trajet).

t_A = d_Acosθ_c/V₁
t_B = d_Bcosθ_c/V₁
t_C = d_Ccosθ_c/V₁ t_AB = AB/V₂+t_A+t_B
t_BC = BC/V₂+t_B+t_C
t_AC = AC/V₂+t_A+t_C t_AB+t_BC-t_AC = 2t_B
p(A,B,t)*p(B,C,t)*p(A,C,-t) = p(B,2t_B) t_AB-t_BC+t_AC = 2AB/V₂+2t_A
p(A,B,t)*p(B,C,-t)*p(A,C,t) = p(B,2AB/V₂+2t_A)

Transformée τ-p

directe	inverse
v(τ,p) = ∫u(t=τ+px, x)dx = ∫∫U(ω,x)e^-iω(τ+px)dωdx = ∫U(ω,k_x=ωp)e^-iωτdω	w(t,x) = ∫v(τ=t-px,p)dp = ∫∫U(ω,k_x=ωp)e^-iω(t-px)dωdp = ∫∫(U(ω,k_x)/\|ω\|)e^-iωte^ik_xxdωdk_x = u(t,x)∗ = ∫(U(ω,x)/\|ω\|)e^-iωtdω U(ω,x) = \|ω\|W(ω,x)

S paration des ondes montantes et descendantes dans l'eau

L'enregistrement simultan une profondeur h dans l'eau de la pression P et de la composante verticale V_z de la vitesse de d placement des particules v fournit des informations spectrales compl mentaires. En effet, les signes du coefficient de r flexion sur la surface libre tant oppos s pour la pression et la vitesse de d placement, un trou dans le spectre de pression dus aux interf rences entre les ondes montantes et les r flexions sur la surface libre (2k_zh+π = (2n+1)π ou f = nV/(2hcosθ)) correspond un maximum pour la vitesse de d placement et inversement. De plus cela permet de s parer les ondes montantes et descendantes au niveau des r cepteurs. En supposant que le coefficient de r flexion pour la pression sur la surface libre est R ( = -1 s'il fait beau, mais ≠ -1 s'il y a des vagues), on a :

eq. ondes et potentiel de vitesse vitesse de d placement pression
ρ∂v/∂t = -gradp v = gradφ p = -ρ∂φ/∂t
Φ = (Φ_m+Φ_d)e^-iωt = (e^-ik_zz+Re^ik_zz)e^-iωt V_z = ik_z (-e^-ik_zz+Re^ik_zz)e^-iωt P = iωρ(e^-ik_zz+Re^ik_zz)e^-iωt
potentiel montant et descendant Φ_m = (1/2)(P/(iωρ)-V_z/(ik_z)) Φ_d = (1/2)(P/(iωρ)+V_z/(ik_z))

Bibliographie et liens

CLAERBOUT J.F. , 1985, Imaging the Earth's interior , Blackwell
YILMAZ O. , 1987, Seismic Data Analysis : Processing, Inversion, and Interpretation of Seismic Data , SEG

Sismique 2D : sources et récepteurs placés le long d'un profil, abscisse ou distance mesur e le long du profil	sources s = x_s	récepteurs g = x_r	point milieu y = (s+g)/2	demi-déport h = (g-s)/2
collections ou sections avant sommation	source commune p(s₀,g,t)	récepteur commun p(s,g₀,t)	point milieu commun p(y₀,h,t)	déport constant p(y,h₀,t)
Exemples de donn es acquises lors de la campagne sismique EW0108 Gulf of Corinth Profil GOC11, effectu e en 2001 sous la responsabilit scientifique de Brian Taylor (University of Hawai'i). Les donn es non trait es (points de tir) sont archiv es au Marine Geoscience Data System, Lamont-Doherty Earth Observatory of Columbia University. Les profils trait s (stacks et migrations) sont archiv s par Shipley, T., Gahagan, L., Johnson, K., and Davis, M., editors, 2005, Seismic Data Center, University of Texas Institute for Geophysics	l gende ptgoc			l gende tr1goc

$cône de diffraction$ l gende cone - cone.m	hyperbole de diffraction en z=0	position du point diffractant à t=0
V²t² = (x-x_m)²+(z-z_m)²	t_d = (1/V)(z_m²+(x-x_m)²)^½	x = x_m , z = z_m
migration de p(x,t) par sommation des diffractions émises à t=0 par chacun des points du sous-sol	sommation sur la courbe de diffraction	image de M = onde(x_m,z_m,t=0)
algorithme de sommation sur trajectoire de diffraction dans le plan xt : ∀(x_m,z_m)	S = ∑_xp(x,t_d(x,x_m,z_m))	p(x_m,z_m) = S

- - l gende cone1 - l gende migsdc - migsdc.m	r flecteur semi-circulaire à t=0 correspondant une impulsion en x = x₀ , t = t₀ z = 0
V²t² = (x-x_m)²+(z-z_m)²	z_m = (V²t₀²-(x₀-x_m)²)^½
algorithme de superposition de 1/2 cercles dans le plan xz : ∀(x₀,t₀)	∀x_m : p(x_m,z_m) = p(x_m,z_m)+p(x₀,t₀)

- l gende fresnel - fresnel.m	tgα = x_F/z_m ≈ α	δl ≈ x_Fsinα ≈ x_F²/z_m	x_F² = πz_m/k = λz_m/2
	tgα = x_Fcos²θ/z_m ≈ α	δl ≈ x_Fcosθsinα ≈ x_F²cos³θ/z_m	x_F² = πz_m/(kcos³θ)

.	onde(x,z,t)	enregistrement en z = 0	image à t = 0
plan d'onde	t = xsin(α)/V + zcos(α)/V	t = xsin(α)/V	z = -xtg(α)/V
relation de dispersion	k_x²+k_z² = ω²/V²	k_x = ωsinθ/V	k_z = -ω(1/V²-k_x²/ω²)^½ (- car onde montante)
onde harmonique = 1 pendage	p(x,z,t) = Pe^{i(k_xx+k_zz-ωt)}	p(x,t) = Pe^i(k_xx-ωt)	p(x,z) = Pe^i(k_xx+k_zz)
superposition d'ondes harmoniques = tous pendages	p(x,z,t) = ∫∫P(k_x,ω)e^{i(k_xx+k_zz-ωt)}dk_xdω	p(x,t) = ∫∫P(k_x,ω)e^i(k_xx-ωt)dk_xdω	p(x,z) = ∫∫P(k_x,ω)e^i(k_xx+k_zz)dk_xdω

TF inverse et directe	dérivation	translation	convolution en x	convolution en k	p réel	p réel	symétrie	dilatation
p(x) = ∫P(k_x)e^ik_xxdk_x	p'(x)	p(x-x₀)	p∗q(x) = ∫p(ξ)q(x-ξ)dξ	p(x)q(x)	p(x)	p(-x)	P(x)	p(ax)
P(k_x) = ∫p(x)e^-ik_xxdx = \|P(k_x)\|e^iχ(k_x)	ik_xP(k_x)	e^-ik_xx₀P(k_x)	P(k_x)Q(k_x)	P∗Q(k_x)	P*(k_x) = P(-k_x)	P*(k_x)	p(-k_x)	(1/\|a\|)P(k_x/a)

p(x)	e^ik₀x	1	cosk₀x	sink₀x	∑e^ink₀x	∑^∞e^ink₀x = ↑λ₀↑
P(k_x)	δ(k_x-k₀)	δ(k_x)	δ(k_x-k₀)+δ(k_x+k₀)	-i(δ(k_x-k₀)-δ(k_x+k₀))	∑δ(k_x-nk₀)	∑^∞δ(k_x-nk₀) = ↑k₀↑

mesure sur [-a,a]	autocorrélation	signe(k_x)	échelon
p(x)Π[-a,a]	∫p(x')p(x+x')dx' = p(x)∗p(-x)	i/x	H(x) = (1+signe(x))/2
P(k_x)∗(2/k_x)sin(k_xa)	P(k_x)P*(k_x) = \|P(k_x)\|²	signe(k_x)	δ(k_x)+1/(ik_x)

r² = x²+y²+z²	k² = ω²/V² = k_x²+k_y²+k_z²	e^ikr/r = ∫∫P(k_x,k_y)e^ik_zze^i(k_xx+k_yy)dk_xdk_y = ∫∫(i/k_z)e^ik_zze^i(k_xx+k_yy)dk_xdk_y
r² = x²+y² , x = rcosθ	κ² = k_x²+k_y² , k_x = κcosη	P(k_x,k_y) = ∫∫e^ikr/re^{-i(k_xx+k_yy)}dxdy = ∫∫e^ikre^{-iκrcos(θ-η)}drdθ
0≤r<∞ , -π≤θ≤π	k_z réel donc κ/k<1	P(k_x,k_y) = ∫dθ∫e^{i(k-κcos(θ-η))r}dr = (i/k)∫dθ/(1-(κ/k)cos(θ-η)) = 2iπ/(k²-κ²)^½ = 2iπ/k_z
a = κ/k , t = tg(α/2)	∫dα/(1-acosα) = 2∫d(tgα/2)/((1-a)+(1+a)tg²α/2) = 2/(1-a)∫dt/(1+((1+a)/(1-a))t²) = 2/(1-a²)^½Arctg(((1+a)/(1-a))^½t) = 2π/(1-a²)^½

onde sur intervalle X	périodisation en x → échantillonnage en k	échantillonnage en x → périodisation en k	longueurs et nombres onde
p(x)	p∗↑X↑	p∗↑X↑.↑Δx↑	λ_x = ∞,X,X/2,..,2Δx
P(k_x)	P.↑2π/X↑	P.↑2π/X↑∗↑2π/Δx↑	±k_x = 0,2π/X,4π/X,..,π/Δx

TF2D	chgt. variable → interpolation (+ pondération)	image à t = 0 par TF2D inverse
P(k_x,ω) = ∫∫p(x,t)e^-i(k_xx-ωt)dxdt	ω = -Vk_z(1+k_x²/k_z²)^½ P(k_x,k_z) = P(k_x,ω(k_x,k_z)) dω/dk_z = A(k_x,k_z) = Vcosθ	p(x,z) = ∫∫(AP)(k_x,k_z)e^i(k_xx+k_zz)dk_xdk_z e^-ik_z(Z-z) = e^{-i(j2pi/Z)(Z-z)} = e^{i(-j2π+k_zz)} = e^ik_zz

calcul de I = ∫e^iφ(k)dk par développement de φ(k) autour de k₀ tel que φ'(k₀) = 0	ordre 0 : φ(k) ≈ φ(k₀) I ≈ e^iφ(k₀)	ordre 2 : φ(k) ≈ φ(k₀)+((k-k₀)²/2)φ''(k₀) I ≈ e^iφ(k₀)∫e^{i((k-k₀)²/2)φ''(k₀)}dk = e^iφ(k₀)(2π/\|φ''(k₀)\|)^½e^{sign_φ''(k₀)iπ/4}
p(x_m,z_m) = ∫∫P(k_x,ω)e^{i(k_xx_m+k_z(k_x,ω)z_m)}dk_xdω = ∫dx∫P(x,ω)dω∫e^iφ(k_x)dk_x φ(k_x) = -k_x(x-x_m)+k_z(k_x)z_m r_d(x) = ((x-x_m)²+z_m²)^½ , t_d(x) = r_d(x)/V , tgθ_d = (x-x_m)/z_m k_x0 = ωsinθ_d/V , k_z(k_x0) = -ωcosθ_d/V , φ(k_x0) = -ωt_d(x)	e^iφ(k_x0) = e^-iωt_d(x) p(x_m,z_m) = ∫dx∫e^-iωt_dP(x,ω)dω = ∫p(x,t_d(x))dx = sommation de p sur hyperbole de diffraction	φ''(k_x) = k_z''(k_x)z_m = z_mV/\|ω\|(1-k_x²V²/ω²)^-3/2 φ''(k_x0) = V(z_m/cos³θ_d)/\|ω\| = V(r_d/cos²θ_d)/\|ω\| ∫e^iφ(k_x)dk_x = V^-½cosθ_dr_d^-½e^iπ/4\|ω\|^½e^-iωt_d(x) p(x_m,z_m) = V^-½∫dxcosθ_dr_d^-½∫dωe^iπ/4\|ω\|^½e^-iωt_d(x)P(x,ω)

$cône de diffraction$ - cone.m	hyperbole de diffraction en z=0	position du point diffractant à t = t_sd
temps direct source-point diffractant : t_sd = (1/V)((x_m-x_s)²+z_m²)^½	t_d = t_sd + (1/V)((x-x_m)²+z_m²)^½	x = x_m , z = z_m
migration de p(x,t) par sommation des diffractions émises par chacun des points du sous-sol au temps t_sd	sommation sur la courbe de diffraction	image de M = onde(x_m,z_m,t_sd)
algorithme de sommation sur trajectoire de diffraction dans le plan xt : ∀(x_m,z_m)	S = ∑_xp(x,t_d(x,x_s,x_m,z_m))	p(x_m,z_m) = S

(S_vG)² = (OS_v)²+(OG)²-2(OS_v)(OG)cos(2α)	(Vt)² = s²+g²-2sgcos(2α)	point milieu fix y₀ , t₀ = 2y₀sinα/V
s = y-h ; g = y+h	(Vt)² = (y-h)²+(y+h)²-2(y²-h²)(cos²α-sin²α) = 4y²sin²α+4h²cos²α	t² = (4y₀²sin²α+4h²cos²α)/V² = t₀²+4h²cos²α/V²

	ellipse de migration E pour une impulsion en y=0 à t	intersection rayon normal à E avec z=0	longueur rayon normal entre point courant M de E et (y₀,0)	dmo.m
t_n² = t²-4h²/V²	y_m²/t²+z_m²/t_n² = V²/4	y₀ = y_m(1-t_n²/t²)	V²t₀²/4 = (y_m-y₀)²+z_m²	t₀²/t_n²+y₀²/h²=1

V(z) = V₀+az	dt = dz/V(z) ω = V(z)k_z(z)	t(z) = ∫(dz/V(z)) = (1/a)Log(1+az/V₀)	V_RMS²(z) = (1/t(z))∫(V(z)dz) = (z/t(z))(V₀+az/2)	V(z) = d(t(z)V_RMS²(z))/dz
V(t) = V₀e^at	dt = dz/V(z) ω = V(z)k_z(z)	z(t) = (V₀/a)(e^at-1)	V_RMS²(t) = (1/t)∫(V²(t)dt) = (V₀²/(2at))((e^2at-1)	V²(t) = d(tV_RMS²(t))/dt

équation iconale	différences finies centrées	opérateur pour Δx = Δz = a	onde conique
(∂T/∂x)²+(∂T/∂z)² = 1/V(x,z)²	(∂T/∂x) = (T(x+Δx,z)-T(x,z)+T(x+Δx,z+Δz)-T(x,z+Δz))/2Δx (∂T/∂z) = (T(x,z+Δz)-T(x,z)+T(x+Δx,z+Δz)-T(x+Δx,z))/2Δz	T(x+Δx,z+Δz) = T(x,z)+(2a²/V(x,z)²-(T(x+Δx,z)-T(x,z+Δz))²)^½	T(x+Δx,z+Δz) = min(T(x+Δx,z),T(x,z+Δz))+a/V(x,z)

relation dispersion	k_z = -ω(1/V²-k_x²/ω²)^½	terme de diffraction	éq. paraxiale (x,z,ω)	éq. paraxiale (x,z,t)
développement 15	k_z ≈ -ω/V(1-V²k_x²/2ω²)	(ik_z)(-iω) = Vk_x²/2	∂P/∂z = (V(x,z)/2iω)∂²P/∂x²	∂²p/∂z∂t = -(V(x,z)/2)∂²p/∂x²
développement 45	k_z ≈ -ω/V(1-(V²k_x²/ω²)/(2-V²k_x²/2ω²))	(ω²-V²k_x²/4)(ik_z) = (iω)Vk_x²/2	(ω²+(V²/4)∂²/∂x²)∂P/∂z = -(iωV/2)∂²P/∂x²	(∂³/∂t²∂z-(V²/4)∂³/∂x²∂z)p = -(V/2)∂³p/∂t∂x²

relation dispersion 15	phase stationnaire	vitesse de groupe = grad(ω(k_x,k_z))	équation du front d'onde elliptique
k_z ≈ -ω/V(1-V²k_x²/2ω²)	x = (∂ω/∂k_x)t z = (∂ω/∂k_z)t	∂ω/∂k_x = (V²k_x/ω)/(1+V²k_x²/2ω²) ∂ω/∂k_z = -V/(1+V²k_x²/2ω²)	x²/2+(z+Vt/2)² = V²t²/4

coefficients des opérateurs de différences finies de l'équation paraxiale à 15 ∑a_iP_i = 0				analyse stabilité pour P = e^ik_xx
explicite (x,z,ω)	P(x,z+Δz) = P(x,z)+(V/2iω)(Δz/Δx²)(P(x-Δx,z)-2P(x,z)+P(x+Δx,z))			P(z+Δz) = P(z)[1-4αsin²(k_xΔx/2)] \|P(z+Δz)\| > \|P(z)\|
α = (V/2iω)(Δz/Δx²)	P(x-Δx, ., ω)	P(x, ., ω)	P(x+Δx, ., ω)
P(., z, ω) P(., z+Δz, ω)	-α 0	2α-1 1	-α 0
implicite (x,z,ω)	P(x,z+Δz) = P(x,z)+(V/2iω)(Δz/2Δx²)(P(x-Δx,z)-2P(x,z)+P(x+Δx,z)+P(x-Δx,z+Δz)-2P(x,z+Δz)+P(x+Δx,z+Δz))			P(z+Δz)[1+4αsin²(k_xΔx/2)] = P(z)[1-4αsin²(k_xΔx/2)] \|P(z+Δz)\| = \|P(z)\|
α = (V/2iω)(Δz/2Δx²)	P(x-Δx, ., ω)	P(x, ., ω)	P(x+Δx, ., ω)
P(., z, ω) P(., z+Δz, ω)	-α -α	2α-1 2α+1	-α -α

implicite (k_x,z,t)	P(z+Δz,t+Δt)-P(z+Δz,t)-P(z,t+Δt)+P(z,t) = (ΔtΔz/4)(Vk_x²/2)(P(z+Δz,t+Δt)+P(z+Δz,t)+P(z,t+Δt)+P(z,t))
α = (Vk_x²/2)(ΔtΔz/4)	P(k_x, . , .)
P(k_x, z , t) P(k_x, z , t+Δt) P(k_x, z+Δz , t) P(k_x, z+Δz , t+Δt)	α-1 α+1 α+1 α-1
implicite (x,z,t)
α = -(V/2)(ΔtΔz/4Δx²)	p(x-Δx, ., .)	p(x, ., .)	p(x+Δx, ., .)
p(., z , t) p(., z , t+Δt) p(., z+Δz , t) p(., z+Δz , t+Δt)	α α α α	-2α-1 -2α+1 -2α+1 -2α-1	α α α α

temps réduit	effet sur les pentes et sur les dérivées partielles	k_z ≈ -ω/V , k'_z ≈ 0	éq. paraxiale 15
t' = t+z/V	dt'/dz = dt/dz + 1/V k'_z/ω = k_z/ω+1/V	k'_z = k_z+ω/V	k'_z = Vk_x²/2ω
t' = t+∫dz/V_M(z)	P(z,t) = P'(z,t'(z,t)) ∂P/∂z = ∂P'/∂z+(1/V_M(z))∂P'/∂t' , ∂P/∂t = ∂P'/∂t' k_z = k'_z-ω/V_M(z)	k'_z = k_z+ω/V_M(z)	k'_z = -ω(1/V(x,z)-1/V_M(z))+Vk_x²/2ω

	eq. ondes vers gauche	eq. ondes	eq. ondes vers droite
1D	(1/V)∂P/∂t = ∂P/∂x -ω/V = k_x	(1/V²)∂²P/∂t² = ∂²P/∂x² (ω/V)² = k_x²	(-1/V)∂P/∂t = ∂P/∂x ω/V = k_x
2D	k_x ≈ -ω/V(1-V²k_z²/2ω²)	(ω/V)² = k_x²+k_z²	k_x ≈ ω/V(1-V²k_z²/2ω²)
paraxiale	Vk_z/ω = -(a-bVk_x/ω)/(1-cVk_x/ω) cosθ_i = (a+bsinθ_i)/(1+csinθ_i)	k_z = -ω/V(1-V²k_z²/ω²)^½	Vk_z/ω = -(a-bVk_x/ω)/(1-cVk_x/ω) cosθ_i = (a-bsinθ_i)/(1-csinθ_i)

interface en x = 0		eq. paraxiale	déplacement et contrainte	continuité en x = 0
x < 0	x' = x	k_z = Vk_x²/2ω	u_y(x) = (e^ik_xx+Re^-ik_xx)e^ik_zz σ_xy(x) = μik_x(e^ik_xx-Re^-ik_xx)e^ik_zz	1+R = T (1-R) = T R = 0 , T = 1
x > 0	x' = x(1+iα/ω) , α>0	k'_x = k_x/(1+iα/ω) k_z = Vk'_x²/2ω	u_y(x') = Te^ik_xx'e^ik_zz σ_xy(x') = (μik_x/(1+iα/ω))Te^ik_xx'e^ik_zz	1+R = T (1-R) = T R = 0 , T = 1

coordonnées sources - récepteurs		coordonnées points-milieux - déports
θ_s = θ-α	θ_g = θ+α	y = (s+g)/2	h = (g-s)/2
∂t/∂s = -sinθ_s/V	∂t/∂g = sinθ_g/V	∂t/∂y = ∂t/∂s+∂t/∂g = 2sinαcosθ/V	∂t/∂h = -∂t/∂s+∂t/∂g = 2cosαsinθ/V
∂t/∂z_s = -cosθ_s/V = -(1-(V∂t/∂s)²)^½/V	∂t/∂z_g = -cosθ_g/V = -(1-(V∂t/∂g)²)^½/V	∂y/∂z = -1/tgα	∂h/∂z = -1/tgθ
∂t/∂z = ∂t/∂z_s+∂t/∂z_g = -2cosαcosθ/V = -((1-(V∂t/∂s)²)^½+(1-(V∂t/∂g)²)^½)/V		∂t/∂z = -((1-(V(∂t/∂y-∂t/∂h)/2)²)^½+(1-(V(∂t/∂y+∂t/∂h)/2)²)^½)/V
k_z/ω = -((1-(Vk_s/ω)²)^½+(1-(Vk_g/ω)²)^½)/V		k_z/ω = -((1-(V(k_y-k_h)/2ω)²)^½+(1-(V(k_y+k_h)/2ω)²)^½)/V
∂P/∂z = (-iω/V)((1-(Vk_s/ω)²)^½+(1-(Vk_g/ω)²)^½)P(k_s,k_g,z,ω)		∂P/∂z = (-iω/V)((1-(V(k_y-k_h)/2ω)²)^½+(1-(V(k_y+k_h)/2ω)²)^½)P(k_y,k_h,z,ω)
∂P/∂z = (( (-iω/V(s))²-∂²/∂s²)^½+( (-iω/V(g))²-∂²/∂g²)^½)P(s,g,z,ω)

	d convolution	d convolution stabilis e	corr lation	corr lation normalis e par l'illumination
R(x,z,ω)	M(x,z,ω)/D(x,z,ω)	M(x,z,ω)D(x,z,ω)/(D(x,z,ω)D(x,z,ω))	M(x,z,ω)D*(x,z,ω)
I(x,z)	∑_s∑_ω(M(x,z,s,ω)/D(x,z,s,ω))	∑_s∑_ω(M(x,z,s,ω)D(x,z,s,ω))/(D(x,z,s,ω)D(x,z,s,ω)+ε²))	∑_s∑_ωM(x,z,s,ω)D*(x,z,s,ω)	∑_s(∑_ω(M(x,z,s,ω)D(x,z,s,ω))/∑_ω(D(x,z,s,ω)D(x,z,s,ω)))

temps d'arriv e en x_m le long du r fracteur	temps diffract depuis le r fracteur	migration par superposition de fronts d'onde
t₀ = d/cosθ_c/V₁+(x_m-dsin(θ_c-α)/cosθ_c)/cosα/V₂	t_d = ((x_g-x_m)²+z_m²)^½/V₁	p(x_m, z_m) = p(x_m, z_m)+p(x, (t₀+t_d)(x, x_m, z_m))

eq. ondes et potentiel de vitesse	vitesse de d placement	pression
ρ∂v/∂t = -gradp	v = gradφ	p = -ρ∂φ/∂t
Φ = (Φ_m+Φ_d)e^-iωt = (e^-ik_zz+Re^ik_zz)e^-iωt	V_z = ik_z (-e^-ik_zz+Re^ik_zz)e^-iωt	P = iωρ(e^-ik_zz+Re^ik_zz)e^-iωt
potentiel montant et descendant	Φ_m = (1/2)(P/(iωρ)-V_z/(ik_z))	Φ_d = (1/2)(P/(iωρ)+V_z/(ik_z))