JMM ex EOST : Ondes sismiques - Imagerie - Traitement

Ondes élastiques : Caractéristiques - Elasticité - Equations d'ondes - Ondes planes - Ondes sphériques
Sismique géométrique : Fronts d'ondes et rayons - Source ponctuelle - V(z) - V(x,y,z)
Réflexion-transmission : Continuité - SH - P/SV surface libre - P/SV interface - Approximations
Ondes guidées : Rayleigh par surface libre et Stoneley par interface - Love et P acoustique dans couche - Rayleigh dans couche - Vitesse de groupe - Love dans stratification
Ondes élastiques + : Ondes cylindriques - Ondes P et S dues à une force ponctuelle - Anisotropie - Atténuation - Saturation en fluide
Réflexion-transmission + : Gradient vitesse - Couche et stratification - Monitoring sismique - Stratification cyclique - Relations réflexion-transmission - Surface ondulée
Documents : Figures, programmes, animations - Sujets exams - Livres et liens

Les vidéos du cours s'ouvrent en cliquant sur les titres de paragraphe.
Les figures grand format s'ouvrent toutes dans la même fenêtre en cliquant sur les icônes.
Les animations Java s'ouvrent en cliquant sur les liens en gras.
Les programmes Matlab écrits pour réaliser les figures sont accessibles en cliquant sur le nom du programme (prog.m) sous l'icône de la figure.

Introduction

Les ondes sismiques sont des ondes élastiques qui se propagent dans la Terre. Pour se familiariser avec la façon dont elles se propagent, il est conseillé de visiter les sites suivants:

Russel D., Acoustics Animations : Longitudinal and Transverse Wave Motion
Le site illustre la propagation 1D d'ondes longitudinales et transverses harmoniques ainsi que celle des ondes de Rayleigh guidées par une surface libre.

Baker S.A. and Wysession M.E., Seismic shear wave propagation : a synthetic animation
On y trouve des animations de la propagation et de la réflexion de fronts d'onde dans le manteau terrestre, et des exemples de tracés de rayons et d'enregistrements.

Tanimoto T., Southern California wavefield reconstruction
Visualisation de la propagation de champs d'ondes enregistrés par un réseau dense de stations sismologiques.

IRIS Earthquake Science, How do seismic waves move across and thru the Earth?

Caractéristiques

Une onde sismique se propage en ondulant (λ = VT), déplace les particules autour de leur position d'équilibre, déforme et contraint le milieu élastique de propagation. Les grandeurs physiques intervenant dans la propagation et leur ordre de grandeur sont les suivants (les vecteurs sont en caractères gras).

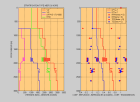
grandeur unité notation composantes ordres de grandeur
longueur d'onde m λ . 10^-3 m (grains dans les roches) - 10⁷ m (taille de la Terre)
période
fréquence
pulsation s
Hz
rad/s T
f = 1/T
ω = 2πf . 10⁶ Hz (ultrasons sur échantillons) - 10^-3 Hz (vibrations propres de la Terre)
vitesses de propagation
ondes P, S m/s V_P
V_S
légende mernord 10² m/s (V_S dans les sols) - 10⁴ m/s (V_P dans le manteau)
V_P/V_S : 1.7 dans les roches consolidées, >10 dans les sols peu consolidés saturés en eau
densité
impédances kg/m³
kg/m²/s ρ
I = ρV 10³ kg/m³ (eau) - 10⁴ kg/m³ (noyau)
déplacement des particules m u u_x , u_y , u_z U : 1 m (glissement sur faille) - 10^-8m (bruit ambiant)
vitesse des particules m/s ∂u/∂t ∂u_x/∂t , ∂u_y/∂t , ∂u_z/∂t U/T - voir les définitions des différentes échelles de magnitudes à partir du rapport U/T
accélération des particules m/s² ∂²u/∂t² ∂²u_x/∂t² , ∂²u_y/∂t² , ∂²u_z/∂t² U/T² : 10 m/s²≈1g (épicentres des grands tremblements de terre) - 10^-11m/s² (vibrations propres de la Terre)
déformations . ε ε_xx , ε_yy , ε_zz
ε_xy , ε_yz , ε_zx U/λ : 10^-6
contraintes Pa σ σ_xx , σ_yy , σ_zz
σ_xy , σ_yz , σ_zx ρV²U/λ = IU/T : 10⁴ - 1 Pa (pressions enregistrées dans l'eau en sismique réflexion, f = 10-100Hz)
direction de propagation . e e_x , e_y , e_z
sinθ , 0 , cosθ les sources sismiques émettent tous azimuts
vecteur d'onde m^-1 k = (2π/λ)e k_x , k_y , k_z caractérise une onde plane harmonique
facteur de qualité . Q . ∞ - 10 (sédiments peu consolidés)

Elasticité linéaire isotrope

Les roches sont des ressorts. Les déformations dues aux ondes sismiques sont suffisamment faibles (sauf au voisinage des sources) pour que les contraintes soient proportionnelles aux déformations. Les coefficients de proportionnalité sont les modules élastiques. Un milieu isotrope (comportement indépendant de l'orientation d'application des contraintes) est caractérisé par deux modules élastiques. Une compression uniaxiale fournit le module d'Young et le coefficient de Poisson de la roche. Les coefficients de Lamé λ et μ sont utilisés pour des états de contrainte-déformation quelconques. L'incompressibilité K est le rapport entre la pression moyenne et la déformation volumique.

. module élastique dilatation cisaillement variation volume
déformation . ε_xx = ∂u_x/∂x ε_xy = (∂u_x/∂y+∂u_y/∂x)/2 divu = ε_xx+ε_yy+ε_zz
compression uniaxiale module Young E
coef. Poisson ν σ_xx = Eε_xx
ε_yy = -νε_xx . divu = (1-2ν)ε_xx
contrainte-déformation quelconque coef. Lamé λ , μ
incompressibilité K σ_xx = λdivu+2με_xx σ_xy = 2με_xy divu = (σ_xx+σ_yy+σ_zz)/3K
relations entre modules E = 10¹⁰ - 10¹¹ Pa
ν = 0.2 - 0.4 (roches) ; 0.5 (eau) λ = Eν/((1+ν)(1-2ν)) μ = E/(2(1+ν)) K = λ+2μ/3 = E/(3(1-2ν))

Voici des valeurs de modules élastiques et densités pour l'air, l'eau et quelques minéraux :

air eau glace calcite
CaCO3 quartz
SiO2 olivine
(Mg,Fe)SiO4
K (GPa) 0.0001 2.4 8.4 70 37 130
μ (GPa) 0 0 3.6 29 44 80
ρ (kg/m³) 1 1000 920 2700 2700 3320

Lorsqu'on utilise des forages, on utilise les coordonnées cylindriques (r,θ,z). Les déformations et les contraintes s'écrivent :

déformations ε_rr = ∂u_r/∂r ε_θθ = (1/r)(u_r+∂u_θ/∂θ) ε_zz = ∂u_z/∂z ε_zr = (∂u_r/∂z+∂u_z/∂r)/2 ε_rθ = ((1/r)(∂u_r/∂θ-u_θ)+∂u_θ/∂r)/2 ε_θz = ((1/r)∂u_z/∂θ+∂u_θ/∂z)/2
contraintes σ_rr = λdivu+2με_rr σ_θθ = λdivu+2με_θθ σ_zz = λdivu+2με_zz σ_zr = 2με_zr σ_rθ = 2με_rθ σ_θz = 2με_θz

avec divu = ε_rr+ε_θθ+ε_zz = (1/r)(∂(ru_r)/∂r+∂u_θ/∂θ)+∂u_z/∂z

Equations des ondes élastiques en milieu homogène isotrope

Deux types d'onde peuvent se propager en milieu élastique isotrope avec des vitesses distinctes. Les ondes de compression, dites ondes P, sont polarisées longitudinalement (le déplacement des particules est orienté dans la direction de propagation). Elles sont les plus rapides. Elles sont l'équivalent en milieu élastique des ondes acoustiques (sons) se propageant dans l'air et l'eau. Les ondes de cisaillement, dites ondes S, sont polarisées transversalement ( le déplacement des particules se fait dans un plan orthogonal à la direction de propagation). Elles n'existent que dans les milieux pouvant être cisaillés élastiquement, donc pas dans les milieux acoustiques. Elles sont plus lentes que les ondes P. Pour des roches compactées (λ ≈ μ ou ν ≈ 0.25), V_P/V_S ≈ 1.7. Mathématiquement, la polarisation correcte des ondes s'obtient automatiquement en écrivant le déplacement des particules comme le gradient d'un potentiel scalaire φ pour les ondes P, ou comme le rotationnel d'un potentiel vecteur ψ pour les ondes S.

Ondes de compression onde longitudinale 1D ondes acoustiques ondes P
déplacement u_x(x,t) u = gradφ(x,t) u = gradφ(x,t)
déformations ε_xx = ∂u_x/∂x divu = Δφ ε_xx = ∂²φ/∂x² , ε_yy , ε_zz
ε_xy = ∂²φ/∂x∂y , ε_yz , ε_zx
contraintes σ_xx = E∂u_x/∂x p = -Kdivu σ_xx = λΔφ+2μ∂²φ/∂x² , σ_yy , σ_zz
σ_xy = 2μ∂²φ/∂x∂y , σ_yz , σ_zx
équations d'équilibre ρ∂²u_x/∂t² = ∂σ_xx/∂x ρ∂²u/∂t² = -gradp ρ∂²u_x/∂t² = ∂σ_xx/∂x+∂σ_xy/∂y+∂σ_xz/∂z
ρ∂/∂x(∂²φ/∂t²) = (λ+2μ)∂/∂x(Δφ)
ρgrad(∂²φ/∂t²) = (λ+2μ)grad(Δφ)
équation des ondes ∂²u_x/∂t² = V_L²∂²u_x/∂x² ∂²p/∂t² = V_A²Δp ∂²φ/∂t² = V_P²Δφ
vitesse de propagation V_L² = E/ρ V_A² = K/ρ V_P² = (λ+2μ)/ρ

Pour des ondes S se propageant dans un plan vertical (c'est le cas lorsque la vitesse de propagation est constante ou qu'elle ne dépend que de la profondeur, comme dans un milieu stratifié horizontement) , il est commode de distinguer deux types de polarisation transverses. Les ondes SH ont une polarisation horizontale perpendiculaire au plan vertical de propagation : le déplacement des particules a une seule composante non nulle. On peut donc écrire directement l'onde en fonction de cette composante. Les ondes SV ont une polarisation transverse dans le plan de propagation : les deux composantes du déplacement des particules s'obtiennent à partir d'un potentiel vecteur ayant une seule composante non-nulle, celle qui est orthogonale au plan de propagation.

Ondes de cisaillement (divu = 0) onde transverse 1D ondes SH (polarisation ⊥ plan de propagation) ondes SV(polarisation dans plan de propagation ⊥ direction de propagation)
déplacement u_y(x,t) u_y(x,z,t) ψ = (0, ψ_y(x,z,t) ,0) , u(x,z,t) = rotψ(x,z,t)
u_x = -∂ψ_y/∂z , u_z = ∂ψ_y/∂x
déformations ε_xy = (1/2)∂u_y/∂x ε_xy = (1/2)∂u_y/∂x , ε_yz ε_xx = -∂²ψ_y/∂z∂x = -ε_zz
ε_xz = (-∂²ψ_y/∂z²+∂²ψ_y/∂x²)/2
contraintes σ_xy = μ∂u_y/∂x σ_xy = μ∂u_y/∂x , σ_yz σ_xx = -2μ∂²ψ_y/∂z∂x = -σ_zz
σ_xz = μ(-∂²ψ_y/∂z²+∂²ψ_y/∂x²)
équations d'équilibre ρ∂²u_y/∂t² = ∂σ_xy/∂x ρ∂²u_y/∂t² = ∂σ_xy/∂x+∂σ_yz/∂z ρ∂²u_x/∂t² = ∂σ_xx/∂x+∂σ_xz/∂z
ρ∂/∂z(∂²ψ_y/∂t²) = μ∂/∂z(∂²ψ_y/∂x²+∂²ψ_y/∂z²)
équation des ondes ∂²u_y/∂t² = V_S²∂²u_y/∂x² ∂²u_y/∂t² = V_S²Δu_y ∂²ψ_y/∂t² = V_S²Δψ_y
vitesse de propagation V_S² = μ/ρ V_S² = μ/ρ V_S² = μ/ρ

Voici des valeurs de vitesses de propagation, coefficients de Poisson et densités pour quelques roches :

grés mal consolidé grés consolidé calcaire granite basalte granulite dunite
V_P (km/s) 2.7 4.1 4.6 6.2 5.9 7.0 8.3
V_S (km/s) 1.4 2.4 2.4 3.7 3.2 3.8 4.8
ν = (V_P²/V_S²-2)/(2V_P²/V_S²-2) 0.32 0.24 0.31 0.22 0.29 0.29 0.25
ρ (kg/m³) 2100 2400 2400 2650 2880 3000 3300

SEG Wiki : vitesses VP pour différentes roches.

Ondes planes

Une onde plane se propage dans une direction e avec une vitesse V_P ou V_S. Le signe des composantes de e détermine le sens de propagation de l'onde dans les trois directions x, y et z. L'équation des ondes laisse toute liberté de choisir n'importe quelle fonction comme solution. Elle n'impose que la forme de la phase pour que l'onde se propage. Une onde plane harmonique correspond au choix d'une solution de type sinusoidal et au choix d'une période de vibration, donc d'une longueur d'onde. On vérifie que la polarisation des ondes P est longitudinale (u // e), celle des ondes S transverse (u ⊥ e).

onde 1D ondes P ondes S
u→ = u(x/V-t)
u← = u(-x/V-t) φ(e.x/V_P-t)
u_longitudinal = gradφ = (e/V_P)φ' ψ(e.x/V_S-t)
u_transverse = rotψ = (e/V_S)∧ψ'
cas harmonique : u = Ue^iω(x/V-t) = Ue^{i2π(x/λ-t/T)} = Ue^i(kx-ωt)
u→ : k = ω/V
u← : k = -ω/V φ = Φe^i(k.x-ωt) , k = (ω/V_P)e
u = ikΦe^i(k.x-ωt) ψ = Ψe^i(k.x-ωt) , k = (ω/V_S)e
u = ik∧Ψe^i(k.x-ωt)

Pour les ondes harmoniques ∂φ/∂x = ik_xφ , ∂φ/∂t = -iωφ . L'équation des ondes devient la relation de dispersion : ω² = (k_x²+k_y²+k_z²)V² . C'est une sphère de rayon 1/V dans les coordonnées (k_x/ω , k_y/ω , k_z/ω). En effet, le milieu étant homogène et isotrope, la vitesse de propagation est la même pour toutes les directions de propagation.
Une onde harmonique occupe tout l'espace avec des oscillations périodiques. Si on l'observe (ou on l'enregistre) dans sa direction de propagation e, on voit sa vraie longueur d'onde λ = 2π/k. Dans une direction différente e', on voit une longueur d'onde apparente supérieure à la vraie longueur d'onde : λ_ae' = λ/cos(angle(e,e')) Le long des axes on observe les longueurs d'onde apparentes λ_x = 2π/k_x , λ_y = 2π/k_y , λ_z = 2π/k_z.

légende ondeP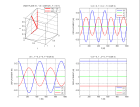
légende ondeSV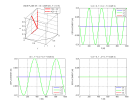
légende ondeSH

Les figures ci-dessus sont obtenues avec le programme ondePS.m.

Ondes sphériques

Les ondes P sphériques émises par une source de compression ponctuelle à symétrie sphérique sont solution d'une équation des ondes 1D pour (rφ(r)).
Le déplacement radial des particules comporte un terme en 1/r, dominant loin de la source, et un terme en 1/r², dominant près de la source.
Pour une onde harmonique, la limite champ proche/lointain est définie par la valeur de kr, c'est à dire par le rapport r/λ.
Pour une source sphérique où le déplacement U₀ est imposé en r = r₀<<λ, on obtient l'amplitude de l'onde en identifiant à U₀ le terme de déplacement en champ proche en r₀.

Δφ(r) = (1/r)∂²(rφ)/∂r² car Δφ(r) = divgradφ(r) = div(∂φ/∂re_r) = grad∂φ/∂r.e_r+∂φ/∂rdive_r = ∂²φ/∂r²+2/r∂φ/∂r (dive_r = 2/r car dive_r = div(r/r) = grad(1/r).r+divr/r et divr = ∂x/∂x+∂y/∂y+∂z/∂z = 3)
∂²(rφ)/∂t² = V_P²∂²(rφ)/∂r² déplacement des particules champ lointain : kr>>1 champ proche : kr<<1
φ = (A/r)f(±r/V_P-t) u = (A/r)e_r(-f/r±f'/V_P) u_cl = (±f'A/rV_P)e_r u_cp = (-Af/r²)e_r
φ = (A/r)e^i(kr-ωt) u = (A/r)e_r(ik-1/r)e^i(kr-ωt) u_cl = (ikA/r)e_re^i(kr-ωt) u_cp = (-A/r²)e_re^i(kr-ωt)
A = -U₀r₀² pour source de rayon r₀<<λ

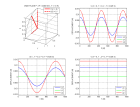
Voici la représentation du déplacement des particules pour une onde P (gauche) et une onde S (droite) sphériques crées par une force ponctuelle imposant un déplacement vertical harmonique à l'origine (ligne magenta).

En champ lointain (ligne du bas), on observe la polarisation radiale de l'onde P et la polarisation transverse de l'onde S ainsi que le diagramme de radiation (variation angulaire d'amplitude) du à l'application d'une force verticale.
En champ proche (ligne du haut), la polarisation est plus complexe.
Le calcul des déplacements est donné au chapitre Ondes P et S dues à une force ponctuelle.

Fronts d'onde et rayons en milieu homogène isotrope

La propagation d'une onde à partir d'un point M quelconque atteint par l'onde à un temps t se fait dans une direction e à la vitesse de propagation V. Un front d'onde correspond à la surface T(x) sur laquelle la perturbation est localisée au temps t. Les rayons représentent les chemins le long duquel l'onde progresse avec la vitesse de propagation propre au milieu. Dans un milieu isotrope homogène, les rayons sont des droites orthogonales aux fronts d'onde. Un front d'onde balaye une direction e' différente de la direction de propagation e avec une vitesse apparente V_ae' supérieure à la vitesse de propagation : V_ae' = V/cos(angle(e,e')). Les vitesses apparentes dans trois directions mutuellement orthogonales sont liées géométriquement par l'équation iconale. La loi de Snell-Descartes exprime l'égalité des vitesses apparentes des fronts d'onde incidents, réfléchis et transmis sur une interface entre deux milieux homogènes (permettant ainsi la continuité des déplacements et contraintes de part et d'autre de l'interface au passage des ondes).

. équation front onde vitesses apparentes le long des axes équation iconale : Pythagore pour les ondes
plan T(x) = e.x/V gradT = e/V e.e=1
gradT.gradT = (∂T/∂x)²+(∂T/∂y)²+(∂T/∂z)² = 1/V²
(1/V_ax)²+(1/V_ay)²+(1/V_az)² = 1/V²
sphérique T(x) = r/V gradT = e_r/V
quelconque T(x) gradT = e_M/V
La propagation des fronts d'onde obéit au principe de Huygens : le front d'onde au temps t+dt est l'enveloppe des ondelettes sphériques de rayon Vdt centrées sur le front d'onde au temps t.
La géométrie des rayons découle du principe de Fermat : le temps de trajet est stationnaire par rapport à toute perturbation de la géométrie du rayon. Par exemple, un trajet réfléchi correspond au minimum des temps de trajets diffractés par les points au voisinage du point de réflexion.
Ces deux principes sont directement utilisables pour déterminer la propagation d'une onde. Ils illustrent concrètement comment une onde trouve sa direction de propagation : elle les essaie toutes et choisit celles pour lesquelles il y a interférence constructive entre trajets voisins.

Source ponctuelle à distance d d'une interface plane : onde directe, réfléchie, conique

Un front d'onde sphérique incident sur une interface plane engendre une onde sphérique réfléchie et une onde transmise. Si la vitesse augmente au passage de l'interface (V₂>V₁), seule la partie du front d'onde sphérique incidente sous des angles inférieurs à l'incidence critique θ_c est transmise. La partie correspondant aux incidences supérieures à l'incidence critique est réfléchie totalement. Le front d'onde transmis, initialement tiré par le front d'onde incident sur l'interface, se propage alors horizontalement sous l'interface à la vitesse V2, supérieure à la vitesse apparente des ondes incidentes et réflechies sur l'interface. Il est en avance par rapport à l'onde incidente et engendre par diffraction un front d'onde conique qui remonte dans le milieu 1 sous l'incidence critique : l'onde conique est le "sillage" dans le milieu 1 de l'onde transmise.
Pour une interface non pentée parallèle à la surface d'enregistrement, la vitesse apparente de l'onde conique en surface est la vitesse de propagation de l'onde transmise le long de l'interface.
Pour une interface pentée faisant un angle α avec la surface d'enregistrement, la vitesse apparente de l'onde conique en surface est différente suivant que les récepteurs sont situés vers l'aval (V_av = V₁/sin(θ_c+α)) ou vers l'amont (V_am = V₁/sin(θ_c-α)) par rapport à la source ponctuelle.

Hodochrone T(X) des ondes directe, réfléchie, conique pour distance source-récepteurs SR=X et milieux homogènes de vitesses V₁ et V₂
pendage α onde directe onde réfléchie
réflexion totale pour incidence θ₁>θ_c onde conique (n'existe que si V₂>V₁)
incidence critique θ_c : sinθ_c = V₁/V₂ ;

légende hodo
direco.m T = X/V₁ T = (4d²+X²)^½/V₁ distance et temps critique : X_c = 2dtgθ_c , T_c = 2d/cosθ_c/V₁
vitesses apparentes horizontale et verticale : V_ax = V₁/sinθ_c = V₂ ; V_az = V₁/cosθ_c
temps de trajet : T = X/V_ax+2d/V_az = X/V₂+2dcosθ_c/V₁

légende hodop T = X/V₁ source virtuelle symétrique de la source par rapport à l'interface
x_v = 2dsinα ; z_v = 2dcosα
T = (4(dcosα)²+(X±2dsinα)²)^½/V₁
+ pour récepteurs vers l'aval
- pour récepteurs vers l'amont
distance critique (triangle source virtuelle, projeté vertical de la SV sur surface, récepteur) :
X_c = 2d(cosαtg(θ_c±α)-±sinα) = 2dsinθ/cos(θ±α)
vitesses apparentes suivant et perpendiculairement à l'interface :
V_aα = V₁/sinθ_c = V₂ ; V_a⊥α = V₁/cosθ_c
distances suivant et perpendiculairement à l'interface :
x_α = Xcosα ; d_⊥α = 2d±Xsinα
temps de trajet : T = x_α/V_aα+d_⊥α/V_a⊥α
T = Xcosα/V₂+(2d±Xsinα)cosθ_c/V₁ = Xsin(θ_c±α)/V₁+2dcosθ_c/V₁

Les figures suivantes illustrent l'effet sur l'hodochrone d'une variation de l'épaisseur d de la couche de vitesse V1 et d'une variation de la vitesse V2.

Si la droite source-récepteurs n'est pas parallèle à la direction de plus grande pente, la propagation se fait dans le plan orthogonal à l'interface passant par SR.
α est le pendage apparent dans le plan de propagation, tel que sinα = sin(pendage)cos(azimut(RS)-azimut(pendage)).

Pour une interface entre deux milieux élastiques, il faut prendre en compte les ondes converties. Voici les figures dessinées par Cagniard en 1939 dans le cas où V_P2>V_S2>V_P1>V_S1.

Pour une source ponctuelle située sur la surface libre d'une couche d'épaisseur d surmontant un demi-espace, les réflexions successives sur l'interface et la surface libre donnent naissance à des réverbérations. Les points de tangence commune entre les réflexions et les ondes coniques multiples sont alignés sur une droite de pente T_c / X_c = V₂/V₁², intermédiaire entre celle des ondes directes et des ondes coniques. (voir aussi ce sujet d'exam).

Ocean Acoustics Library : propagation des ondes directe, réfléchie, transmise, conique est une animation qui permet de comprendre la physique de l'interaction d'une onde sphérique avec une interface plane.
Heelan P.A., 1953, On the theory of head waves
Mitchell J.F. et R.J. Bolander, 1986, Structural interpretation using refraction velocities from marine seismic surveys montrent un bel enregistrement d'un point de tir en mer :

Lorsque la profondeur de l'interface change latéralement, la méthode "plus-minus" permet de déterminer la variation latérale du temps de trajet dans la couche, proportionnelle à la profondeur de l'interface.
Pour deux tirs direct A et inverse C enregistrés sur les mêmes capteurs, l'addition les temps de trajet des ondes coniques enregistrés au capteur B situé entre A et C permet de déterminer le temps de trajet t_B entre l'interface et le capteur.
Leur soustraction permet de déterminer la vitesse V₂ sous l'interface.

t_A = d_Acosθ_c/V₁
t_B = d_Bcosθ_c/V₁
t_C = d_Ccosθ_c/V₁ t_AB = AB/V₂+t_A+t_B
t_BC = BC/V₂+t_B+t_C
t_AC = AC/V₂+t_A+t_C t_AB+t_BC-t_AC = 2t_B t_AB-t_BC+t_AC = 2AB/V₂+2t_A

Hagedoorn, J. G., 1959, The Plus-Minus method of interpreting seismic refraction sections

Rayons, distances et temps de propagation pour V(z) - V_RMS : stratification - gradient de vitesse - gradient et couches

Si la vitesse de propagation ne dépend que de la profondeur (stratification horizontale ou gradient vertical de vitesse), la géométrie des rayons est déterminée par la loi de Snell : le paramètre p d'un rayon (inverse de la vitesse apparente horizontale de l'onde) est constant. L'angle d'incidence θ(z) du rayon par rapport à la verticale augmente ou diminue avec l'augmentation ou la diminution de vitesse.
La distance horizontale X(p) parcourue le long d'un rayon et le temps de propagation T(p) s'expriment en fonction du paramètre p en sommant sur les intervalles de profondeur correspondant à l'épaisseur des couches dans un milieu stratifié.
En complément à la représentation de l'hodochrone T(X), il est utile de représenter le plan τ-p, où τ(p) = T(p)-pX(p) représente le temps vertical de propagation dans la stratification pour un rayon de paramètre p.

loi de Snell : p = sinθ/V = (1/V_ax) = cte pour un rayon paramètre du rayon distance horizontale X(p) entre deux points d'un même rayon temps de trajet T(p) entre deux points d'un même rayon
stratification plane horizontale (couches d'épaisseur d_i et vitesses constantes V_i)
-
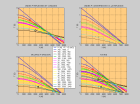légende hodostratif - hodostratif.m - hodostrat.m réflexion
p = sinθ_i/V_i X(p) = ∑d_itgθ_i = p∑d_iV_i/(1-p²V_i²)^½ T(p) = ∑d_i/cosθ_iV_i = ∑d_i/(1-p²V_i²)^½V_i
τ(p) = T(p)-pX(p) = ∑d_icosθ_i/V_i = ∑d_i(1-p²V_i²)^½/V_i
conique
p = sinθ_i/V_i = 1/V_n X_cn = 2∑d_itgθ_i = 2∑d_i/(V_n²/V_i²-1)^½ si V_n > V_i, i = 1 à n-1
T = X/V_n+2∑d_icosθ_i/V_i = X/V_n+2∑d_i(1/V_i²-1/V_n²)^½ pour X > X_cn

Cette figure montre que pour une couche peu épaisse, l'onde conique générée par l'onde transmise dans cette couche n'est pas observée en première arrivée.

Dans un milieu à gradient de vitesse (comme sur ces mesures de VP et VS faites dans un forage de 300 m sous le fond de la mer) , la sommation discrète est remplacée par une intégration sur des intervalles d'épaisseur dz.
Si le gradient de vitesse a est constant (V(z) = V₀+az), les rayons sont des arcs de cercle. La construction géométrique des rayons et le calcul de X(p) et T(p) dans ce cas se font simplement car les arcs de cercle correspondant aux différents paramètres sont tous centrés sur la droite V(z) = 0.
Dans ce cas, les fronts d'onde sont aussi des cercles orthogonaux à la famille de cercles des rayons. Ils sont tous centrés sur l'axe Oz à des profondeurs croissantes avec le temps de propagation.
Si on se limite à des angles d'incidence petits, on peut approximer T(X) entre deux profondeurs sous une forme hyperbolique analogue à celle dans un milieu de vitesse constante. La vitesse moyenne du milieu équivalent est V_RMS, couramment utilisée dans le traitement des données de sismique réflexion.

loi de Snell : p = sinθ/V = (1/V_ax) = cte pour un rayon paramètre du rayon distance horizontale X(p) entre deux points d'un même rayon temps de trajet T(p) entre deux points d'un même rayon
gradient de vitesse V(z) (pour un gradient positif, un rayon atteint une profondeur maximum Z_max(p)) p = sinθ(z)/V(z) = 1/V(Z_max) X(p) = p∫dzV(z)/(1-p²V(z)²)^½ T(p) = ∫dz/(1-p²V(z)²)^½V(z)
τ(p) = ∫dz(1-p²V(z)²)^½/V(z)
cas V(z) = V₀+az : les rayons sismiques sont des cercles de rayon R(p)=1/(ap) centrés sur la droite V(z) = 0 sinθ(z) = (V₀/a+z)/R = pV(z) X(p) = R[cosθ] = R[(1-p²V(z)²)^½] T(p) = ∫Rdθ/V(z(θ)) = (1/a)∫dθ/sinθ = (1/a)[Log(tg(θ/2))] = (1/a)[Log(pV(z)/(1+(1-p²V(z)²)^½))]
cas V(z) = V₀+az : les fronts d'onde à T = -(1/a)[Log(tg(θ₀/2))] sont des cercles orthogonaux aux rayons d'équation x²+(z-Z_max(T))² = X(T)²

légende hodovz - hodovz.m tg(θ₀/2) = e^-aT X(T) = V₀/atgθ₀ = (V₀/2a)(e^aT-e^-aT)
X(T) = (V₀/a)sh(aT)
Z_max(T) = (V₀/a)(1/sinθ₀-1) = (V₀/2a)(e^aT+e^-aT-2)
Z_max(T) = (V₀/a)(ch(aT)-1)
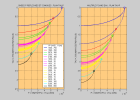
la formule d'Herglotz-Wiechert permet de déterminer Z(V(z)) à partir de l'hodochrone X(p), T(p) (voir cette présentation de J.Virieux en pages 30-35 pour le calcul de la formule) p = dT/dX Z_max(p_m = 1/V_m) = V_m/π∫dpX(p)/(p²V_m²-1)^½
l'intégrale étant calculée dans l'intervalle [p₀ = 1/V(z=0) = (dT/dX)(X=0) , p_m = 1/V_m]
cas V(z) = V₀+az : la mesure simultanée de X(p), T(p) et dT/dX = p pour une valeur de p permet de déterminer V₀ et a
p = sin(θ₀)/V₀ = 1/V(Z_max) la fonction f(p) = pX(p)/T(p) - cosθ/Log(tg(θ/2)) = 0 pour θ = θ₀ d'où V₀ = sin(θ₀)/p et a = cosθ₀/(pX(p))
approximation V_RMS pour propagation subverticale

vrms.m θ ≈ 0
p ≈ θ_i/V_i X(p) ≈ p∑d_iV_i T(p) ≈ ∑d_i(1+p²V_i²/2)/V_i = ∑d_i/V_i+(p²/2)∑d_iV_i = T(X=0)+X²/2∑d_iV_i
T(X)² ≈ T(0)²+X²/V_RMS²
V_RMS² = (∑d_iV_i)/(∑d_i/V_i) = (∫V(z)dz)/(∫dz/V(z))
V_RMS(V₀+az) = (a(V₀z+az²/2)/Log(1+az/V₀))½

En général, V augmente régulièrement avec z. Les rayons issus d'une source ponctuelle, courbés vers la surface, émergent à des distances horizontales croissantes pour des incidences θ₀ décroissant de 90° à 0°. Le front d'onde arrive avec une vitesse apparente horizontale croissante en surface.
Si le gradient de vitesse augmente fortement dans un intervalle de profondeur, l'hodochrone présente une triplication
Si le gradient change de signe dans un intervalle de profondeur, il se forme une zone d'ombre : aucun rayon n'émerge dans l'intervalle de X correspondant.
Si la source de trouve dans la zone de faible vitesse, il se forme un guide d'onde pour les rayons quittant la source avec des incidences telles que le point bas (ou haut) du rayon est aussi dans la zone.
Un front d'onde plan incident sur une zone où V augmente avec z est totalement réfléchi si la zone contient le point bas des rayons.

- -
légende hodovzto - hodovzt.m - hodovzo.m

Voici les rayons et l'hodochrone pour un modèle comportant une couche d'épaisseur d où V(z) = V₀+az sur un demi-espace de vitesse V₂>V₁=V₀+ad et la figure correspondante.
Une simulation de la propagation des ondes dans un milieu comportant une couche sur un demi-espace avec un gradient de vitesse dans la couche et le demi-espace et une discontinuité de vitesse sur l'interface est disponible sur ces diapositives.

Lutter W.J., R. D. Catchings and C. M. Jarchow, 1994, An image of the Columbia Plateau from inversion of high-resolution seismic data montrent l'effet d'une stratification basalte (5 km/s) - sédiment (4 km/s) -socle (5.5 km/s) sur les premières arrivées.
Hornby B., 1993, Tomographic reconstruction of near-borehole slowness using refracted borehole sonic arrivals est un exemple d'utilisation d'ondes coniques et réfractées en diagraphie.
Russel D., Réfraction du son dans l'atmosphère
Garcés, M.A., Hansen, R. A. & Lindquist, K.G., 1998, Traveltimes for infrasonic waves propagating in a stratified atmosphere

Rayons, fronts d'onde, amplitude pour V(x,y,z) : pendage - rayons 3D

Pour un milieu stratifié comportant des couches séparées par des interfaces pentées, on ne dispose plus d'une normale commune à toutes les interfaces. La loi de Snell s'écrit pour chaque interface en fonction de la direction du rayon incident e et de la normale à l'interface n. Les rayons réfléchis et transmis sont contenus dans le plan (e , n). Soit m le vecteur normal à n dans le plan (e , n), θ₁ l'angle d'incidence par rapport à n), e_r et e_t les directions des rayons réfléchi et transmis, θ₂ l'angle (e_t , n)

e = -cosθ₁n+sinθ₁m e_r = cosθ₁n+sinθ₁m e_r-e = 2cosθ₁n = -2(e.n)n e_r = e-2(e.n)n
e/V₁ = -cosθ₁/V₁n+sinθ₁/V₁m e_t/V₂ = -cosθ₂/V₂n+sinθ₂/V₂m e_t/V₂-e/V₁ = (cosθ₁/V₁-cosθ₂/V₂)n e_t = V₂/V₁(e-(e.n+((V₁/V₂)²-(1-e.n²))^½)n)

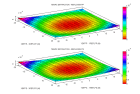
Voici un exemple pour un modèle comportant deux interfaces planes pentées. L'interface supérieure est la limite sédiments-socle. L'interface inférieure est le réflecteur dans le socle. Les trajets correspondent à des réflexions PP et PS sur le réflecteur pour une source et un récepteur placés à la limite sédiments-socle. La point de réflexion PP est l'intersection du segment source virtuelle-récepteur avec le réflecteur. Le point de réflexion PS est sur l'intersection du plan de propagation PP avec le réflecteur. Il correspond au temps minimum pour des trajets PS diffractés pour des points diffractants PS situés sur ce segment. Les rayons transmis dans les sédiments émergent en des points différents à la surface.

- -
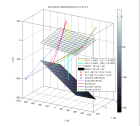légende refl3d - refl3d.m

Si la vitesse de propagation varie continuement avec la profondeur et latéralement, les vitesses apparentes horizontales et verticales varient le long d'un même rayon. La variation le long d'un rayon de l'inverse d'une vitesse apparente dans une direction est égale à la composante du gradient de 1/V dans cette direction. Cette relation permet de déterminer la géométrie 3D des rayons par intégration en ajustant à chaque pas d'abscisse curviligne s la direction de propagation e et en parcourant la distance ds = Vdt dans cette direction.
Dans la cas où V(x,z) varie linéairement avec x et z, les rayons sismiques sont des arcs de cercles centrés sur la droite V(x,z) = 0.

s abscisse curviligne d'un rayon x(s)
e = dx/ds équation différentielle des rayons
e.e = 1 , e.∂e/∂x = 0 , gradT.∂e/∂x = 0
∂(dT/ds)/∂x = ∂(e.gradT)/∂x = e.grad∂T/∂x = d(∂T/∂x)/ds courbure des rayons
de/ds = e_N/R torsion des rayons
b = e∧e_N
de_N/ds = -e/R-b/τ
gradT = e/V
T = ∫ds/V(x(s)) d(e/V)/ds = d(gradT)/ds = grad(dT/ds) = grad(1/V) 1/R = Ve_N.grad(1/V) 1/τ = -Rb.d(Vgrad(1/V))/ds
cas V(x,z) = V₀+a_xx+a_zz = V₀+a(xsinα+zcosα)
par une rotation d'angle α, on se ramène au cas V(Z) = V₀+aZ
les rayons sismiques sont des cercles centrés sur la droite V(x,z) = 0 d(sinθ/V)/ds = -a_x/V² = -asinα/V²
d(cosθ/V)/ds = -a_z/V² = -acosα/V² 1/R = dθ/ds = -a_xcosθ/V+a_zsinθ/V = asin(θ-α)/V

En cherchant une solution à l'équation des ondes avec une vitesse V(x) sous forme d'une onde harmonique quasi-plane portée par un front d'onde d'équation T(x) et ayant une amplitude A(x), on obtient des termes dépendant des puissances successives de la pulsation. Le terme en ω², dominant à haute fréquence, donne l'équation iconale des temps de trajet. Le terme en ω donne l'équation de transport permettant de calculer l'amplitude A(x).

onde quasi plane (solution haute fréquence de l'éq. des ondes terme en ω² → éq.iconale terme en ω → éq. transport tube de rayon de section dS(s)
φ = A(x)e^iω(T(x)-t) gradT.gradT=1/V² 2gradA.gradT+AΔT = div(A²gradT) = 0 ∫∫∫div(A²gradT)dυ = ∫∫(A²/V)e.dσ = 0
A²dS/V = cte

Langan, R.T., I. Lerche, and R. T. Cutler, 1985, Tracing of rays through heterogeneous media: An accurate and efficient procedure
Bernasconi G. and G. Drufuca, 2001, 3-D traveltimes and amplitudes by gridded rays proposent une méthode simple de tracé de rayons 3D par une méthode de différences finies.
Sava P. and S. Fomel, M. 2001, 3-D traveltime computation using Huygens wavefront tracing montrent comment le principe de Huygens permet de déterminer des fronts d'onde et temps de trajets.

Continuité des déplacements et des contraintes sur une interface plane

On obtient les coefficients de réflexion-transmission des ondes élastiques sur une interface plane entre deux milieux élastiques en écrivant les conditions de continuité des composantes du déplacement et des contraintes qui s'appliquent sur l'interface de part et d'autre de l'interface. Les contraintes qui ne s'appliquent pas sur l'interface n'interviennent pas dans les conditions de continuité. Pour une surface libre, les contraintes sont nulles hors du milieu élastique et doivent donc s'annuler sur la surface libre. Par contre, le déplacement de la surface libre est quelconque (parfois destructeur).
Les calculs sont faits avec des ondes planes harmoniques pour lesquelles la fréquence et la longueur d'onde apparente horizontale sont identiques pour l'onde incidente et les ondes réfléchies et transmises (loi de Snell). Les valeurs de k_z pour chaque onde dépendent de sa nature (P ou S), de son angle d'incidence (les angles sont liés par la loi de Snell), et de son sens de propagation vertical (montante ou descendante) qui fixe le signe de k_z.
Voici les différents cas possible suivant l'interface et la nature des ondes se propageant dans le plan vertical (x,z) et incidentes sur une interface plane horizontale :

ω et k_x = ωp = ωsin(θ)/V_P = ωsin(η)/V_S de l'onde incidente sont les mêmes pour toutes les ondes réfléchies et transmises sur une interface plane horizontale
ondes descendantes : k_z^P = +ωcos(θ)/V_P , k_z^S = +ωcos(η)/V_S
ondes montantes : k_z^P = -ωcos(θ)/V_P , k_z^S = -ωcos(η)/V_S ondes SH ondes P-SV
surface libre σ_zy^{Incidente SH}+σ_zy^{Réfléchie SH} = 0 σ_zz^{Incidente P ou SV}+σ_zz^{Réfléchie P}+σ_zz^{Réfléchie SV} = 0
σ_zx^{Incidente P ou SV}+σ_zx^{Réfléchie P}+σ_zx^{Réfléchie SV} = 0
interface solide - solide u_y^{Incidente SH}+u_y^{Réfléchie SH} = u_y^{Transmise SH}
σ_zy^{Incidente SH}+σ_zy^{Réfléchie SH} = σ_zy^{Transmise SH} u_x^{Incidente P ou SV}+u_x^{Réfléchie P}+u_x^{Réfléchie SV} = u_x^{Transmise P}+u_x^{Transmise SV}
u_z^{Incidente P ou SV}+u_z^{Réfléchie P}+u_z^{Réfléchie SV} = u_z^{Transmise P}+u_z^{Transmise SV}
σ_zz^{Incidente P ou SV}+σ_zz^{Réfléchie P}+σ_zz^{Réfléchie SV} = σ_zz^{Transmise P}+σ_zz^{Transmise SV}
σ_zx^{Incidente P ou SV}+σ_zx^{Réfléchie P}+σ_zx^{Réfléchie SV} = σ_zx^{Transmise P}+σ_zx^{Transmise SV}
interface liquide - solide . u_z^{Incidente P}+u_z^{Réfléchie P} = u_z^{Transmise P}+u_z^{Transmise SV}
σ_zz^{Incidente P}+σ_zz^{Réfléchie P} = σ_zz^{Transmise P}+σ_zz^{Transmise SV}
σ_zx^{Transmise P}+σ_zx^{Transmise SV} = 0

Réflexion d'une onde plane harmonique SH sur une interface plane

Une onde plane harmonique SH se propageant dans le plan vertical (x,z), incidente sur une interface plane horizontale entre deux milieux élastiques, provoque sur cette interface une perturbation du déplacement u_y et de la contrainte de cisaillement σ_zy. Cette perturbation balaye l'interface à la vitesse apparente horizontale de l'onde incidente V_S1/sinη₁, où η₁ est l'angle du rayon incident par rapport à la verticale. Elle est équilibrée par les perturbations dues aux ondes SH réfléchie et transmise qui balayent l'interface à la même vitesse apparente horizontale (loi de Snell). Le déplacement u_y et la contrainte σ_zy résultant des ondes SH incidente et réfléchie d'un coté de l'interface sont égaux à u_y et σ_zy dus à l'onde SH transmise de l'autre coté de l'interface. On obtient ainsi les coefficients de réflexion et transmission, définis ici pour le déplacement des particules.
Dans le cas où V_S1>V_S2 et η₁>η_c, l'onde transmise devient évanescente : son amplitude décroit exponentiellement avec la distance à l'interface. La réflexion totale s'accompagne d'un déphasage χ à la réflexion donné par l'argument du coefficient de réflexion complexe. La somme de l'onde incidente et de l'onde réfléchie totalement produit une onde stationnaire verticalement et progressive horizontalement.

loi de Snell :
k_x = ωp = ωsinη₁/V_S1 = ωsinη₂/V_S2 onde incidente SH descendante onde réfléchie SH montante onde transmise SH descendante
déplacement onde SH
u_y(x,z,t) = U_ye^ik_zze^i(k_xx-ωt) U_y^I = 1
k_z^I = ωcosη₁/V_S1 U_y^R = R
k_z^R = -ωcosη₁/V_S1 U_y^T = T
k_z^T = ωcosη₂/V_S2
contrainte sur surface horizontale
σ_zy(x,z,t) = μ∂u_y/∂z = ρV_S²ik_zu_y = iωS_zye^ik_zze^i(k_xx-ωt) S_zy^I = ρ₁V_S1cosη₁ S_zy^R = -ρ₁V_S1cosη₁R S_zy^T = ρ₂V_S2cosη₂T
continuité sur interface z =0
(u_y^I+u_y^R)(z=0) = u_y^T(z=0)
(σ_zy^I+σ_zy^R)(z=0) = σ_zy^T(z=0) 1+R=T
(1-R)ρ₁V_S1cosη₁ = Tρ₂V_S2cosη₂ R = (ρ₁V_S1cosη₁-ρ₂V_S2cosη₂)/(ρ₁V_S1cosη₁+ρ₂V_S2cosη₂) T = 2ρ₁V_S1cosη₁/(ρ₁V_S1cosη₁+ρ₂V_S2cosη₂)
faible contraste
ρ+δρ , V+δV
δη = tgηδV/V (δp=0) R ≈ -δ(ρVcosη)/2ρVcosη = -(1/2)(δρ/ρ+(1-tg²η)δV/V) T ≈ 1
réflexion totale
sinη_c=V_S1/V_S2
η₁>η_c , pV_S2>1 k_z^R = -k_z^I = -ω(1-p²V_S1²)^½/V_S1
R = (ρ₁V_S1(1-p²V_S1²)^½-iρ₂V_S2(p²V_S2²-1)^½)/(ρ₁V_S1(1-p²V_S1²)^½+iρ₂V_S2(p²V_S2²-1)^½)
R = e^iχ(p) , χ(p) = -2Arctg(ρ₂V_S2(p²V_S2²-1)^½/ρ₁V_S1(1-p²V_S1²)^½)
(u_y^I+u_y^R)(x,z,t) = (e^{ik_z^Iz}+e^{i(k_z^Rz+χ(p))})e^i(k_xx-ωt) = 2cos(k_z^Iz-χ(p)/2)e^{i(k_xx-ωt+χ(p)/2)} onde transmise évanescente : k_z^T = iω(p²V_S2²-1)^½/V_S2
T = 2ρ₁V_S1(1-p²V_S1²)^½/(ρ₁V_S1(1-p²V_S1²)^½+iρ₂V_S2(p²V_S2²-1)^½)
T = ||T||e^iχ(p)/2
u_y^T(x,z,t) = ||T||e^{-ωz(p²V_S2²-1)^½/V_S2}e^{i(k_xx-ωt+χ(p)/2)}

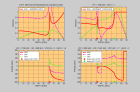
Voici les coefficients de réflexion et transmission et le déplacement obtenus pour des angles d'incidence croissant dans le cas de la réflexion partielle et totale avec le programme reflsh.m.

légende reflsh
légende reflsht

Voici une animation dans le cas de la réflexion sur une surface libre (R=1) qui produit des noeuds de vibration (contrainte) pour z = nπ/k_z et des ventres pour z = (n+1/2)π/k_z.

De même, dans le cas acoustique, les coefficients de réflexion-transmission sur une interface plane s'obtiennent pour le potentiel de déplacement φ(x,z,t) en écrivant la continuité de la composante verticale du déplacement u_z et de la pression sur l'interface.

loi de Snell :
k_x = ωp = ωsinθ₁/V_P1 = ωsinθ₂/V_P2 onde incidente P descendante onde réfléchie P montante onde transmise P descendante
déplacement u_z onde P
u_z(x,z,t) = ∂φ/∂z = Φik_zφ Φ^I = 1
k_z^I = ωcosθ₁/V_P1 Φ^R = R
k_z^R = -ωcosθ₁/V_P1 Φ^T = T
k_z^T = ωcosθ₂/V_P2
pression σ sur interface
σ(x,z,t) = -KΔφ = ρV_P²k²φ = ω²Sφ S^I = ρ₁ S^R = ρ₁R S^T = ρ₂T
continuité sur interface z =0
(u_z^I+u_z^R)(z=0) = u_z^T(z=0)
(σ^I+σ^R)(z=0) = σ^T(z=0) (1-R)cosθ₁/V_P1 = Tcosθ₂/V_P2
(1+R)ρ₁ = Tρ₂ R = (ρ₂V_P2cosθ₁-ρ₁V_P1cosθ₂)/(ρ₁V_P1cosθ₂+ρ₂V_P2cosθ₁)
u_z^R/u_z^I = -R T = 2ρ₁V_P2cosθ₁/(ρ₁V_P1cosθ₂+ρ₂V_P2cosθ₁)
réflexion totale
sinθ_c=V_P1/V_P2
θ₁>θ_c , pV_P2>1 k_z^R = -k_z^I = -ω(1-p²V_P1²)^½/V_P1
R = (ρ₂V_P2(1-p²V_P1²)^½-iρ₁V_P1(p²V_P2²-1)^½)/(ρ₂V_P2(1-p²V_P1²)^½+iρ₁V_P1(p²V_P2²-1)^½)
R = e^iχ(p) , χ(p) = -2Arctg(ρ₁V_P1(p²V_P2²-1)^½/ρ₂V_P2(1-p²V_P1²)^½) onde transmise évanescente : k_z^T = iω(p²V_P2²-1)^½/V_P2

Ocean Acoustics Library : réflexion totale d'une onde plane sur une interface plane

Réflexion d'une onde plane harmonique P ou SV sur une surface plane libre

Les ondes P et SV se propageant dans le plan vertical (x,z) exercent une compression σ_zz et un cisaillement σ_zx sur la surface libre horizontale d'un demi-espace. Elles sont donc couplées à la réflexion : une onde P ou SV incidente se réfléchit sous forme d'une onde P et d'une onde SV. Les contraintes σ_zz et σ_zx résultant de l'onde incidente et des deux ondes réfléchies doivent s'annuler sur la surface libre. On obtient ainsi les coefficients de réflexion sur la surface libre, définis ici pour les potentiels de déplacement des particules.
Dans le cas où une onde SV est incidente avec un angle η supérieur à l'incidence critique correspondant au rapport V_S/V_P, l'onde P réfléchie par la surface libre devient évanescente. L'onde SV est totalement réfléchie avec un déphasage χ' à la réflexion donné par l'argument du coefficient de réflexion complexe.

loi de Snell :
k_x = ωp = ωsinθ/V_P = ωsinη/V_S onde incidente P montante onde réfléchie P descendante onde réfléchie SV descendante
potentiels de déplacement P et SV
φ(x,z,t) = Φ e^{ik_z^Pz}e^i(k_xx-ωt)
ψ_y(x,z,t) = Ψ e^{ik_z^Sz}e^i(k_xx-ωt) Φ^I = 1
k_z^P = -ωcosθ/V_P Φ^R = R_φ
k_z^P = ωcosθ/V_P Ψ^R = R_ψ
k_z^S = ωcosη/V_S
contraintes exercées par onde P sur une surface horizontale
σ_zz^P = λΔφ+2μ∂²φ/∂z² = -ρω²(1-2p²V_S²)φ = ρω²S_zze^{ik_z^Pz}e^i(k_xx-ωt)
σ_zx^P = 2μ∂²φ/∂z∂x = -2ρV_S²ωpk_zφ = ρω²S_zxe^{ik_z^Pz}e^i(k_xx-ωt) S_zz = -(1-2p²V_S²)
S_zx = 2V_S²pcosθ/V_P S_zz = -(1-2p²V_S²)R_φ
S_zx = -(2V_S²pcosθ/V_P)R_φ .
contraintes exercées par onde SV sur une surface horizontale
σ_zz^S = 2μ∂²ψ_y/∂z∂x = -2ρV_S²ωpk_zψ = ρω²S_zze^{ik_z^Sz}e^i(k_xx-ωt)
σ_zx^S = μ(-∂²ψ_y/∂z²+∂²ψ_y/∂x²) = ρω²(1-2p²V_S²)ψ = ρω²S_zxe^{ik_z^Sz}e^i(k_xx-ωt) . . S_zz = -(2V_S²pcosη/V_S)R_ψ
S_zx = (1-2p²V_S²)R_ψ
onde P incidente, contraintes nulles sur surface libre z = 0
(σ_zz^PI + σ_zz^PR + σ_zz^SR)(z=0) = 0
(σ_zx^PI + σ_zx^PR + σ_zx^SR)(z=0) = 0 (1-2p²V_S²)(1+R_φ)+(2V_S²pcosη/V_S)R_ψ = 0
(2V_S²pcosθ/V_P)(1-R_φ)+(1-2p²V_S²)R_ψ = 0

légende reflps D = (1-2p²V_S²)²+4V_S⁴p²cosθ/V_Pcosη/V_S
R_φ = (-(1-2p²V_S²)²+4V_S⁴p²cosθ/V_Pcosη/V_S)/D
R_ψ = (-4(1-2p²V_S²)V_S²pcosθ/V_P)/D
onde SV incidente, contraintes nulles sur surface libre z = 0
(σ_zz^SI + σ_zz^PR + σ_zz^SR)(z=0) = 0
(σ_zx^SI + σ_zx^PR + σ_zx^SR)(z=0) = 0 (1-2p²V_S²)R'_φ+(2V_S²pcosη/V_S)(-1+R'_ψ) = 0
-(2V_S²pcosθ/V_P)R'_φ+(1-2p²V_S²)(1+R'_ψ) = 0

légende reflps R'_φ = (4(1-2p²V_S²)V_S²pcosη/V_S)/D
R'_ψ = (-(1-2p²V_S²)²+4V_S⁴p²cosθ/V_Pcosη/V_S))/D
réflexion totale de l'onde SV , sinη > V_S/V_P (η > 36°)
onde P réfléchie évanescente : k_z^P = iω(p²V_P²-1)^½/V_P R'_ψ = e^iχ'(p)
χ'(p) = -2Arctg((4V_S⁴p²(p²V_P²-1)^½/V_Pcosη/V_S)/(1-2p²V_S²)²)

Réflexion d'une onde plane harmonique P ou SV sur une interface plane

Sur une interface plane horizontale entre deux demi-espaces élastiques, les ondes P et SV se propageant dans le plan vertical (x,z) sont reliées par la loi de Snell et par la continuité des composantes du déplacement u_x et u_z et des contraintes σ_zz et σ_zx de part et d'autre de l'interface. Une onde incidente P ou SV génère deux ondes P et SV réfléchies et deux ondes P ou SV transmises. Les quatre équations de continuité s'écrivent sous forme d'une matrice multipliée par le vecteur des coefficients de réflexion-transmission, définis ici pour les potentiels de déplacement des particules.
Pour une interface liquide-solide, il y a continuité de u_z et σ_zz de part et d'autre de l'interface et le cisaillement σ_zx dans le milieu élastique doit s'annuler à l'interface.
Dés que l'angle d'incidence est supérieur à une valeur d'incidence critique, l'onde pour laquelle la valeur d'incidence est supérieure à 90° devient évanescente. Les coefficients de réflexion-transmission deviennent complexes. Le déphasage χ' à la réflexion totale de l'onde SV est donné par l'argument du coefficient de réflexion.

loi de Snell : k_x = ωp = ωsinθ₁/V_P₁ = ωsinη₁/V_S₁ = ωsinθ₂/V_P₂ = ωsinη₂/V_S₂
P incidente descendante
Φ^I = 1
k_z^I = ωcosθ₁/V_P1 P réfléchie montante
Φ^R = R_φ
k_z^P = -ωcosθ₁/V_P1 SV réfléchie montante
Ψ^R = R_ψ
k_z^S = -ωcosη₁/V_S1 P transmise descendante
Φ^T = T_φ
k_z^P = ωcosθ₂/V_P2 SV transmise descendante
Ψ^T = T_ψ
k_z^S = ωcosη₂/V_S2
U_x = p + pR_φ + (cosη₁/V_S1)R_ψ = pT_φ -(cosη₂/V_S2)T_ψ
U_z = cosθ₁/V_P1 -(cosθ₁/V_P1)R_φ + pR_ψ = (cosθ₂/V_P2)T_φ + pT_ψ
S_zz = ρ₁(1-2p²V_S1²) + ρ₁(1-2p²V_S1²)R_φ - (2ρ₁V_S1²pcosη₁/V_S1)R_ψ = ρ₂(1-2p²V_S2²)T_φ + (2ρ₂V_S2²pcosη₂/V_S2)T_ψ
S_zx = -2ρ₁V_S1²pcosθ₁/V_P1 + (2ρ₁V_S1²pcosθ₁/V_P1)R_φ + ρ₁(1-2p²V_S1²)R_ψ = -(2ρ₂V_S2²pcosθ₂/V_P2)T_φ + ρ₂(1-2p²V_S2²)T_ψ
écriture matricielle
cas liquide-solide AR = B ; R = [R_φ , R_ψ , T_φ , T_ψ]^t ; B = [-p , -cosθ₁/V_P1 , -ρ₁(1-2p²V_S1²) , 2ρ₁V_S1²pcosθ₁/V_P1]^t
A_LR_L = B_L ; R_L = [R_φ , T_φ , T_ψ]^t ; B_L = [-cosθ₁/V_P1 , -ρ₁ , 0]^t
A[4,4]
A_L[3,3] p cosη₁/V_S1 -p cosη₂/V_S2
-cosθ₁/V_P1 p -cosθ₂/V_P2 -p
ρ₁(1-2p²V_S1²) (ρ₁) -2ρ₁V_S1²pcosη₁/V_S1 -ρ₂(1-2p²V_S2²) -2ρ₂V_S2²pcosη₂/V_S2
2ρ₁V_S1²pcosθ₁/V_P1 (0) ρ₁(1-2p²V_S1²) 2ρ₂V_S2²pcosθ₂/V_P2 -ρ₂(1-2p²V_S2²)
P incidente descendante ou montante

légende reflpsv - reflpsv.m R_φ = det([B,A[:,2:4]])/det(A)
t_φ = det([b,A[:,2:4]])/det(A)
R_ψ = det([A[:,1],B,A[:,3:4]])/det(A)
t_ψ = det([A[:,1],b,A[:,3:4]])/det(A)
T_φ = det([A[:,1:2],B,A[:,4]])/det(A)
r_φ = det([A[:,1:2],b,A[:,4]])/det(A)
T_ψ = det([A[:,1:3],B])/det(A)
r_ψ = det([A[:,1:3],b])/det(A)
P incidente descendante
D = det(A) = P-Q
R_φ = (-P-Q)/D
R_ψ =2S/D AR = B ; R = [R_φ , R_ψ , T_φ , T_ψ]^t ;
B = [-p , -cosθ₁/V_P1 , -ρ₁(1-2p²V_S1²) , 2ρ₁V_S1²pcosθ₁/V_P1]^t = [-a₁₁ , a₂₁ , -a₃₁ , a₄₁]^t ;
D = (a₁₁A₁₁+a₃₁A₃₁)-(a₂₁A₂₁+a₄₁A₄₁) ;
DR_φ = -(a₁₁A₁₁+a₃₁A₃₁)-(a₂₁A₂₁+a₄₁A₄₁)
DR_ψ/2 = a₁₁a₂₁(a₃₃a₄₄-a₄₃a₃₄) +a₁₁a₄₁(a₂₃a₃₄-a₃₃a₂₄) +a₃₁a₄₁(a₁₃a₂₄-a₂₃a₁₄)
DT_φ/2 = -(a₁₁a₂₁(a₃₂a₄₄-a₄₂a₃₄) +a₁₁a₄₁(a₂₂a₃₄-a₃₂a₂₄) +a₃₁a₄₁(a₁₂a₂₄-a₂₂a₁₄))
DT_ψ/2 = (a₁₁a₂₁(a₃₂a₄₃-a₄₂a₃₃) +a₁₁a₄₁(a₂₂a₃₃-a₃₂a₂₃) +a₃₁a₄₁(a₁₂a₂₃-a₂₂a₁₃)
P incidente montante
k_z^I = -ωcosθ₂/V_P2 Ar = b ; r = [t^φ,t^ψ,r^φ,r^ψ]^t
b = [p , -cosθ₂/V_P2 , ρ₂(1-2p²V_S2²) , 2ρ₂V_S2²pcosθ₂/V_P2]^t = [-a₁₃ , a₂₃ , -a₃₃ , a₄₃]^t
D = (a₁₃A₁₃+a₃₃A₃₃)-(a₂₃A₂₃+a₄₃A₄₃) ;
Dr_φ = -(a₁₃A₁₃+a₃₃A₃₃)-(a₂₃A₂₃+a₄₃A₄₃)
Dr_ψ/2 = a₁₃a₂₃(a₃₁a₄₂-a₄₁a₃₂) +a₁₃a₄₃(a₂₁a₃₂-a₃₁a₂₂) +a₃₃a₄₃(a₁₁a₂₂-a₂₁a₁₂)
Dt_φ/2 = -(a₁₃a₂₃(a₃₄a₄₂-a₄₄a₃₂) +a₁₃a₄₃(a₂₄a₃₂-a₃₄a₂₂) +a₃₃a₄₃(a₁₄a₂₂-a₂₄a₁₂))
Dt_ψ/2 = a₁₃a₂₃(a₃₄a₄₁-a₄₄a₃₁) +a₁₃a₄₃(a₂₄a₃₁-a₃₄a₂₁) +a₃₃a₄₃(a₁₄a₂₁-a₂₄a₁₁)
cas liquide-solide

reflpsl.m A_LR_L = B_L ; R_L = [R_φL , T_φL , T_ψL]^t ; B_L = [-cosθ₁/V_P1 , -ρ₁ , 0]^t
A_Lr_L = b_L ; r_L = [t_φL , r_φL , r_ψL]^t ; b_L = [-cosθ₂/V_P2 , ρ₂(1-2p²V_S2²) , 2ρ₂V_S2²pcosθ₂/V_P2]^t
D_L = -ρ₂²cosθ₁/V_P1((1-2p²V_S2²)²+4V_S2⁴p²cosθ₂/V_P2cosη₂/V_S2) -ρ₁ρ₂cosθ₂/V_P2
D_LR_φL = -ρ₂²cosθ₁/V_P1((1-2p²V_S2²)²+4V_S2⁴p²cosθ₂/V_P2cosη₂/V_S2) +ρ₁ρ₂cosθ₂/V_P2
D_LT_φL = -2ρ₁ρ₂cosθ₁/V_P1(1-2p²V_S2²) ; D_Lt_φL = -2ρ₂²cosθ₂/V_P2(1-2p²V_S2²)
D_LT_ψL = -4ρ₁ρ₂cosθ₁/V_P1V_S2²pcosθ₂/V_P2
SV incidente descendante ou montante

reflpsv.m R'_φ = det([B',A[:,2:4]])/D
t'_φ = det([b',A[:,2:4]])/D
R'_ψ = det([A[:,1],B',A[:,3:4]])/D
t'_ψ = det([A[:,1],b',A[:,3:4]])/D
T'_φ = det([A[:,1:2],B',A[:,4]])/D
r'_φ = det([A[:,1:2],b',A[:,4]])/D
T'_ψ = det([A[:,1:3],B'])/D
r'_ψ = det([A[:,1:3],b'])/D
SV incidente descendante
Ψ^I = 1 ; k_z^I = ωcosη₁/V_S1
D = det(A) = -P'+Q'
R'_ψ = (-P'-Q')/D AR'=B' ; R' = [R'_φ , R'_ψ , T'_φ , T'_ψ]^t ;
B' = [cosη₁/V_S1 , -p , -2ρ₁V_S1²pcosη₁/V_S1 , -ρ₁(1-2p²V_S1²)]^t = [a₁₂ , -a₂₂ , a₃₂ , -a₄₂]^t ;
D = -(a₁₂A₁₂+a₃₂A₃₂)+(a₂₂A₂₂+a₄₂A₄₂) ;
DR'_ψ = -(a₁₂A₁₂+a₃₂A₃₂)-(a₂₂A₂₂+a₄₂A₄₂)
SV incidente montante
k_z^I = -ωcosη₂/V_S2 Ar'=b' ; r' = [t'_φ , t'_ψ , r'_φ , r'_ψ]^t
b' = [cosη₂/V_S2 , p , -2ρ₂V_S2²pcosη₂/V_S2 , ρ₂(1-2p²V_S2²)]^t = [a₁₄ , -a₂₄ , a₃₄ , -a₄₄]^t ;
D = -(a₁₄A₁₄+a₃₄A₃₄)+(a₂₄A₂₄+a₄₄A₄₄)
Dr'_ψ = -(a₁₄A₁₄+a₃₄A₃₄)-(a₂₄A₂₄+a₄₄A₄₄)
réflexion totale de l'onde SV descendante
p = sinη₁/V_S₁
1/V_S1 > p > 1/V_P1
p > 1/V_S2 > 1/V_P2
R'_ψ = e^iχ'(p) termes de A imaginaires : a₁₄ = i(p²V_S2²-1)^½/V_S2 ; a₂₁ = -i(p²V_P1²-1)^½/V_P1 ; a₂₃ = -i(p²V_P2²-1)^½/V_P2 ;
a₃₄ = -2iρ₂V_S2²p(p²V_S2²-1)^½/V_S2 ; a₄₁ = 2iρ₁V_S1²p(p²V_P1²-1)^½/V_P1 ; a₄₃ = 2iρ₂V_S2²p(p²V_P2²-1)^½/V_P2 ;
⇒ A₁₂, A₃₂ et P' sont imaginaires purs, A₁₂, A₃₂ et Q' sont réels
R'_ψ = (-P'-Q')/(-P'+Q') = e^iχ'(p)
χ'(p) = 2Arctg(P'/iQ') = 2Arctg((1/i)(a₁₂A₁₂+a₃₂A₃₂)/(a₂₂A₂₂+a₄₂A₄₂))

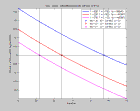
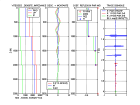
Voici les coefficients de réflexion-transmission P-SV et SV-P calculés pour des angles d'incidence 0°, 15° et 30° dans l'eau pour un modèle de vitesses-densité stratifié type Mer du Nord :
-

Approximations des coefficients de réflexion P-P et P-SV pour faibles contrastes

Lorsque les paramètres élastiques et la densité varient peu au passage d'une interface plane, les coefficients de réflexion s'expriment linéairement en fonction des variations relatives de ces paramètres. Ces expressions approximées sont utilisées dans l'analyse des amplitudes en sismique réflexion.

faibles contrastes ρ₂ = ρ+δρ ; V_P₂ = V_P+δV_P ; θ₂ = θ+δθ ; δθ = tgθδV_P/V_P ; V_S₂ = V_S+δV_S ; η₂ = η + δη ; δη = tgηδV_S/V_S
a₁₁ = -a₁₃ = a₂₂ = -a₂₄ = p ; a₁₂ = cosη/V_S ; a₂₁ = -cosθ/V_P ; a₃₁ = a₄₂ = ρ(1-2p²V_S²) ; a₃₂ = -2ρV_S²pcosη/V_S ; a₄₁ = 2ρV_S²pcosθ/V_P
a₁₄ = (a₁₂+δa₁₂) ; a₂₃ = (a₂₁+δa₂₁) ; a₃₃ = a₄₄ = -(a₃₁+δa₃₁) ; a₃₄ = (a₃₂+δa₃₂) ; a₄₃ = (a₄₁+δa₄₁)
D = det(A) D = (p²-a₂₁a₁₂)(a₃₁²-a₄₁a₃₂) - (2pa₂₁)(-2a₃₁a₃₂) + (-p²-a₂₁a₁₂)(a₃₂a₄₁+a₃₁²) + (a₁₂a₂₁+p²)(-a₃₁²-a₄₁a₃₂) - (-2pa₁₂)(2a₃₁a₄₁) + (p²-a₂₁a₁₂)(a₃₁²-a₄₁a₃₂)
D = 2(p²-a₂₁a₁₂)(a₃₁²-a₄₁a₃₂) -2(p²+a₂₁a₁₂)(a₃₂a₄₁+a₃₁²) +4pa₃₁(a₂₁a₃₂+a₁₂a₄₁) = -4p²a₄₁a₃₂ -4a₂₁a₁₂a₃₁² +4pa₃₁(a₂₁a₃₂+a₁₂a₄₁)
D = 4cosθ/V_Pcosη/V_S [p²(2ρV_S²p)² +(ρ(1-2p²V_S²))² +4ρ²p²V_S²(1-2p²V_S²)] = 4ρ²cosθ/V_Pcosη/V_S
R_φ DR_φ = (-p²-a₂₁a₁₂)((a₃₁+δa₃₁)²-(a₄₁+δa₄₁)(a₃₂+δa₃₂)) - (-p(a₂₁+δa₂₁)+pa₂₁)(-a₃₂(a₃₁+δa₃₁)-a₃₁(a₃₂+δa₃₂)) + (p²-a₂₁(a₁₂+δa₁₂))(a₃₂(a₄₁+δa₄₁)+a₃₁(a₃₁+δa₃₁)) + (a₁₂(a₂₁+δa₂₁)+p²)(a₃₁(a₃₁+δa₃₁)-a₄₁(a₃₂+δa₃₂)) - (-pa₁₂-p(a₁₂+δa₁₂))(-a₃₁(a₄₁+δa₄₁)+a₄₁(a₃₁+δa₃₁)) + (p²-(a₂₁+δa₂₁)(a₁₂+δa₁₂))(-a₃₁²-a₄₁a₃₂))
DR_φ = (-p²-a₂₁a₁₂)(2a₃₁δa₃₁-a₄₁δa₃₂-a₃₂δa₄₁) - 2pa₃₂a₃₁δa₂₁ + (p²-a₂₁a₁₂)(a₃₂δa₄₁+a₃₁δa₃₁)-a₂₁δa₁₂(a₃₂a₄₁+a₃₁²) + (p²+a₁₂a₂₁)(a₃₁δa₃₁-a₄₁δa₃₂)+a₁₂δa₂₁(a₃₁²-a₄₁a₃₂) + 2pa₁₂(-a₃₁δa₄₁+a₄₁δa₃₁) + (a₂₁δa₁₂+a₁₂δa₂₁)(a₃₁²+a₄₁a₃₂)
DR_φ = 2(p(pa₃₂-a₁₂a₃₁)δa₄₁ + a₁₂(pa₄₁-a₂₁a₃₁)δa₃₁ + a₃₁(a₃₁a₁₂-pa₃₂)δa₂₁)
DR_φ = 2ρ(-2p²cosη/V_Sδ(ρV_S²cosθ/V_P) +cosη/V_Scosθ/V_Pδ(ρ(1-2p²V_S²) + ρ(1-2p²V_S²)cosη/V_Sδ(-cosθ/V_P))
DR_φ = 2ρcosη/V_S(cosθ/V_P((1-4p²V_S²)δρ - 4ρp²δ(V_S²)) - ρδ(cosθ/V_P))
R_φ = (1/2)((1-4p²V_S²)δρ/ρ - 8p²V_S²δV_S/V_S - δ(cosθ/V_P)/(cosθ/V_P))
R_φ = (1/2)((1-4p²V_S²)δρ/ρ - 8p²V_S²δV_S/V_S + (1/cosθ)²δV_P/V_P)
R_φ = (1/2)((δρ/ρ+δV_P/V_P) + (δV_P/V_P -4V_S²/V_P²(δρ/ρ+2δV_S/V_S)sin²θ + (tg²θ-sin²θ)δV_P/V_P) ≈ R₀+Gsin²θ
R_ψ DR_ψ = (2pa₂₁)((a₃₁+δa₃₁)²-(a₄₁+δa₄₁)(a₃₂+δa₃₂)) - p((a₂₁+δa₂₁)+a₂₁)(a₃₁(a₃₁+δa₃₁)-a₄₁(a₃₂+δa₃₂)) + (-p²-a₂₁(a₁₂+δa₁₂))(-a₃₁(a₄₁+δa₄₁)+a₄₁(a₃₁+δa₃₁)) + p(-(a₂₁+δa₂₁)+a₂₁)(-a₃₁(a₃₁+δa₃₁)-a₄₁(a₃₂+δa₃₂)) - (p²-a₂₁(a₁₂+δa₁₂))(a₃₁(a₄₁+δa₄₁)+a₄₁(a₃₁+δa₃₁)) + (p²-(a₂₁+δa₂₁)(a₁₂+δa₁₂))(2a₃₁a₄₁)
DR_ψ = 2pa₂₁(2a₃₁δa₃₁-a₄₁δa₃₂-a₃₂δa₄₁) - 2pa₂₁(a₃₁δa₃₁-a₄₁δa₃₂)-pδa₂₁(a₃₁²-a₄₁a₃₂) + (-p²-a₂₁a₁₂)(-a₃₁δa₄₁)+a₄₁δa₃₁)) + (-pδa₂₁)(-a₃₁²-a₄₁a₃₂) - (p²-a₂₁a₁₂)(a₃₁δa₄₁+a₄₁δa₃₁) +a₂₁δa₁₂2a₃₁a₄₁ + (-2a₃₁a₄₁(a₂₁δa₁₂+a₁₂δa₂₁))
DR_ψ = 2(p(a₂₁a₃₁-pa₄₁)δa₃₁ + a₂₁(-pa₃₂+a₁₂a₃₁)δa₄₁ + a₄₁(pa₃₂-a₃₁a₁₂)δa₂₁)
DR_ψ = -2ρpcosθ/V_P(δ(ρ(1-2p²V_S²)) + cosη/V_Sδ(2ρV_S²cosθ/V_P) + 2ρV_S²cosη/V_Sδ(-cosθ/V_P))
DR_ψ = -2ρpcosθ/V_P ((1-2p²V_S²+2V_S²cosθ/V_Pcosη/V_S)δρ + 2ρ(-p²+cosη/V_Scosθ/V_P)δ(V_S²)
R_ψ = -(1/2)pV_S/cosη ((1-2p²V_S²+2V_S²cosθ/V_Pcosη/V_S)δρ/ρ + 4V_S²(-p²+cosη/V_Scosθ/V_P)δV_S/V_S)
R_ψ ≈ -(1/2)sinη ((1+2V_S/V_P)δρ/ρ + 4V_S/V_PδV_S/V_S) pour incidence faible

Onde de Rayleigh guidée par une surface libre et de Stoneley guidée par une interface

L' onde de Rayleigh correspond à la propagation le long de la surface libre d'un demi-espace (z ≥ 0 ) de deux ondes P et SV évanescentes de même vitesse de propagation horizontale V_R < V_S. L'annulation des contraintes sur la surface libre fixe V_R. V_R est fonction du rapport V_P/V_S et est indépendante de la fréquence (V_R ≈ 0.9V_S). Le déplacement des particules en surface est elliptique rétrograde car il existe un déphasage de π/2 entre les composantes u_x et u_z.

1/V_R = p = k_x/ω > 1/V_S > 1/V_P onde P évanescente
k_z^P = iω(p²V_P²-1)^½/V_P onde S évanescente
k_z^S = iω(p²V_S²-1)^½/V_S
σ_zz = σ_zx = 0 sur surface libre z = 0 (1-2p²V_S²)Φ+i2pV_S(p²V_S²-1)^½Ψ = 0
-i2V_S²p(p²V_P²-1)^½/V_PΦ+(1-2p²V_S²)Ψ = 0

légende rayleq déterminant = 0
(1-2p²V_S²)²-4p²V_S⁴(p²V_S²-1)^½/V_S(p²V_P²-1)^½/V_P = 0
(2-V_R²/V_S²)²-4(1-V_R²/V_P²)^½(1-V_R²/V_S²)^½ = 0
(V_R²/V_S²)³-8(V_R²/V_S²)²+4(6-4V_S²/V_P²)V_R²/V_S²+16(V_S²/V_P²-1) = 0 solutions réelles de x³+bx²+cx+d = 0
A = (3c-b²)/9 ; B = (9bc-27d-2b³)/54 ; Δ = A³+B²
si Δ > 0 , C³ = B+Δ^½ ; D³ = B-Δ^½ ; x = C+D-b/3
si Δ = 0, x = 2B^⅓-b/3 ; x = -B^⅓-b/3
si Δ < 0 , θ = arccos(B/(-A³)^½) ; x = 2(-A)^½cos((θ+2nπ)/3)-b/3 avec n = 0,1,2

légende rayleigh
(u_x , u_z) = (U_x(z) , U_z(z))e^iω(x/V_R-t) U_x = iωpΦe^{-ωz(p²V_P²-1)^½/V_P}+ω(p²V_S²-1)^½/V_SΨe^{-ωz(p²V_S²-1)^½/V_S}
U_z = -ω(p²V_P²-1)^½/V_PΦe^{-ωz(p²V_P²-1)^½/V_P}+iωpΨe^{-ωz(p²V_S²-1)^½/V_S}
U_x = e^iπ/2ωpΦ(e^{-ωz(p²V_P²-1)^½/V_P}+(1/(2p²V_S²)-1)e^{-ωz(p²V_S²-1)^½/V_S})
U_z = e^iπω(p²V_P²-1)^½/V_PΦ(e^{-ωz(p²V_P²-1)^½/V_P}+(1/(2p²V_S²)-1)^-1e^{-ωz(p²V_S²-1)^½/V_S})

Les racines complexes de l'équation du 3ème degré obtenue en annulant le déterminant de Rayleigh correspondent à des ondes guidées de vitesse intermédiaire entre V_P et V_S qui s'atténuent rapidement avec la distance source-récepteur (voir Gao et al., 2014).

Abel J. Simulation de la propagation d'une onde de Rayleigh

De même, une interface (z = 0) entre deux demi-espaces élastiques peut guider une onde de Stoneley (seulement pour certaines valeurs des rapports de vitesses et densités). Elle est constituée de deux ondes de Rayleigh couplées (deux ondes P₁, SV₁ évanescentes pour z ≤ 0 couplées à deux ondes P₂ , SV₂ évanescentes pour z ≥ 0) se propageant à la même vitesse horizontale V_ST < V_S1. V_ST est déterminée par l'annulation du déterminant de la matrice A obtenue lors du calcul des coefficients de réflexion-transmission pour les ondes P-SV. Il n'existe pas toujours une solution, sauf pour une interface liquide-solide. Dans ce cas, lorque la vitesse des ondes S dans le solide est inférieure à la vitesse des ondes P dans le liquide ("slow formation"), la vitesse de l'onde de Stoneley est proche de celle de V_S dans le solide.

eq. de Stoneley
interf. liq-sol.
D_L = -ρ₂²cosθ₁/V_P1((1-2p²V_S2²)²+4V_S2⁴p²cosθ₂/V_P2cosη₂/V_S2) -ρ₁ρ₂cosθ₂/V_P2 = 0
(1-2p²V_S2²)²-4V_S2⁴p²(p²V_P2²-1)^½/V_P2(p²V_S2²-1)^½/V_S2 + (ρ₁/ρ₂)((p²V_P2²-1)^½/V_P2)/((p²V_P1²-1)^½/V_P1) = 0

Biot, M.A., 1952, Propagation of elastic waves in a cylindrical bore containing a fluid calcule les vitesses de propagation des ondes de Rayleigh et Stoneley dans le cas d'un forage.
Stephen, R.A., F. Cardo-Casas, and C. H. Cheng , 1985, Finite-difference synthetic acoustic logs montrent la propagation d'une onde de Stoneley dans un puits pour une diagraphie acoustique.

Ondes de Love et P acoustique guidées dans une couche d'épaisseur H

L'onde de Love est une onde guidée formée par interférence constructive d'ondes SH réfléchies totalement dans une couche de vitesse V_S1 surmontant un demi-espace de vitesse V_S2>V_S1. La réflexion sur la surface libre se fait sans déphasage, celle sur l'interface avec un déphasage χ , obtenu lors du calcul du coefficient de réflexion d'une onde SH pour un angle d'incidence dans la couche supérieur à η_c. La vitesse de propagation V_L de l'onde de Love est la vitesse apparente horizontale des ondes SH dans la couche, telle que V_S1≤V_L≤V_S2. Elle dépend de la fréquence (dispersion). Les différents modes propres s'établissant verticalement dans la couche (mode fondamental et harmoniques) correspondent à une surface libre placée sur les noeuds (contrainte) ou les ventres (déplacement) de la vibration stationnaire imposée par la réflexion totale sur l'interface. Ils correspondent à des incidences différentes des ondes SH rebondissant dans la couche, donc à des courbes de dispersion distinctes.

légende love onde stationnaire en z
k_z pour modes propres onde progressive en x , k_x = (ω²/V_S²-k_z²)^½
vitesse de phase V(ω) = V_ax = ω/k_x ω ≥ fréquence de coupure ω_c
k_x réel pour onde progressive en x
modes propres 1D
do, do, sol, do, mi, sol... e^ikz+e^-ikz = 2cos(kz)
Hk_n = nπ , nλ_n/2 = H , n = 1,2,3...
plaque à bords libres
R_sup = R_inf = 1 e^ik_zz+e^-ik_zz = 2cos(k_zz)
Hk_{z n} = nπ , nλ_{z n}/2 = H , n = 1,2,3... k_{x n} = (ω²/V_S²-(nπ/H)²)^½
V_n(ω) = ω/k_{x n} ω_{c n} = nπV_S/H
couche (-H ≤ z ≤ 0)
sur 1/2 espace (z≥ 0)
R_surf = 1 ; R_interf = e^iχ(p) e^ik_1zz+e^iχ(p)e^-ik_1zz = 2e^iχ(p)/2cos(k_1zz-χ(p)/2)
Hk_{1z n}+χ(p)/2 = nπ , n = 0,1,2,3... k_{x n} = (ω²/V_S1²-(nπ-χ(p)/2)²/H²)^½
V_{L n}(ω) = ω/k_{x n} = 1/p_n k_{x nc} = ω_{c n}/V_S2 ; χ(1/V_S2) = 0
ω_{c n} = nπ/(H(1/V_S1²-1/V_S2²)^½)

légende lovdisp - displov.m k_1z = (ω/V_S1)(1-p²V_S1²)^½
χ(p) = -2Arctg(ρ₂V_S2(p²V_S2²-1)^½/ρ₁V_S1(1-p²V_S1²)^½) = -2Arctg(I₂/I₁)
relation de dispersion de l'onde de Love :
ω(p_n) = (-χ(p_n)/2+nπ)V_S1/(H(1-p_n²V_S1²)^½) = (Arctg(I₂/I₁)+nπ)V_S1/(H(1-p_n²V_S1²)^½)

Uieda L., Simulation de la propagation d'ondes SH issue d'une source ponctuelle dans une couche

La dispersion d'une onde guidée P acoustique formée par les interférences constructives de réflexion multiples P se propageant dans une couche sous une incidence supérieure à l'incidence critique s'obtient de même en utilisant le déphasage à la réflexion calculé pour l'onde acoustique.
En tenant compte du fait que le coefficient de réflexion pour le déplacement u_z est l'opposé de celui du potentiel (déphasage supplémentaire de π), la condition d'interférence constructive s'écrit :
2k_zH+χ(p)+π = 2nπ avec k_z = ωcosθ₁/V_P1 et χ(p) = -2Arctg(ρ₁V_P1(p²V_P2²-1)^½/ρ₂V_P2(1-p²V_P1²)^½)
D'où la relation de dispersion reliant la vitesse de propagation horizontale de l'onde guidée 1/p_n à la fréquence : ω(p_n) = ((2n-1)π-χ(p_n))V_P1/(2H(1-p_n²V_P1²)^½)
Les fréquences de coupures pour les différents modes s'écrivent avec p = 1/V_P2 et χ(1/V_P2) = 0 : ω_{c n} = (2n-1)π/(2H(1/V_P1²-1/V_P2²)^½)

Ondes de Rayleigh guidées dans une couche d'épaisseur H

Une onde SV totalement réfléchie dans une couche telle que V_S1<V_S2<V_P1<V_P2 engendre une onde guidée de Rayleigh se propageant à la vitesse V_R telle que V_S1≤V_R≤V_S2. La réflexion totale sur la surface libre produit un déphasage χ'₁(p) obtenu lors du calcul des coefficients de réflexion P-SV sur une surface libre. Celle à l'interface avec le demi-espace produit un déphasage χ'₂(p) obtenu lors du calcul des coefficients à l'interface. On établit la relation de dispersion en tenant compte de la somme χ'₁₂(p) de ces deux déphasages dans l'écriture du mode propre vertical dans la couche. On obtient ainsi les courbes de dispersion des harmoniques (n≥1 , V_S1≤V_Rn≤V_S2, V_Rn=V_S2 à la fréquence de coupure f_cn) de l'onde de Rayleigh guidée par la couche.

conditions aux limites modes propres en z onde progressive en x fréquence de coupure
R_surf = e^iχ'₁(p)
R_interf = e^iχ'₂(p)
χ'₁₂(p) = χ'₁(p)+χ'₂(p) (n-χ'₁₂(p)/2π)λ_{1z n}/2 = H
Hk_{1z n}+χ'₁₂(p)/2 = nπ k_{x n} = (ω²/V_S1²-(nπ-χ'₁₂(p)/2)²/H²)^½
V_{R n}(ω) = ω/k_{x n} = 1/p_n ω_{c n} = (nπ-χ'₁₂(1/V_S2))/2)/(H(1/V_S1²-1/V_S2²)^½)
rel. dispersion Rayleigh
harmoniques n≥1
V_S1≤V_{R n}≤V_S2 χ'₁(p) = -2Arctg((4V_S1⁴p²(p²V_P1²-1)^½/V_P1(1-p²V_S1²)^½/V_S1)/(1-2p²V_S1²)²) = -2Arctg(S)
χ'₂(p) = -2Arctg(Im(D)/Re(D)) = -2Arctg(I)
tg(Hω(1-p²V_S1²)^½/V_S1) = -tg((χ'₁(p)+χ'₂(p))/2) = (I+S)/(1-IS)
ω(p_n) = (-(χ'₁(p_n)+χ'₂(p_n))/2+nπ)V_S1/(H(1-p_n²V_S1²)^½) = (Arctg((I+S)/(1-IS))+nπ)V_S1/(H(1-p_n²V_S1²)^½)

La courbe de dispersion du mode fondamental de l'onde de Rayleigh est obtenue en considérant quatre ondes P et SV montantes et descendantes dans la couche et deux ondes P et SV évanescentes dans le demi-espace. La vitesse de propagation V_R0 correspond à l'annulation du déterminant de la matrice des conditions aux limites sur la surface libre en z = -H et sur l'interface en z = 0 (condition d'interférence constructive). Elle est telle que V_RS1≤V_R0≤V_RS2 où V_RS1 est la vitesse de l'onde de Rayleigh guidée à la surface libre d'un demi-espace de vitesse V_S1 et V_RS2 celle pour un demi-espace de vitesse V_S2. A basse fréquence, V_R0 = V_RS2 (l'onde de longueur d'onde >> H ne voit pas la couche).

cond. limites descendante P1 , k_zP1 = ω(1-p²V_P1²)^½/V_P1
Z_P1 = e^-ik_zP1H descendante S1 , k_zS1 = ω(1-p²V_S1²)^½/V_S1
Z_S1 = e^-ik_zS1H montante P1 , -k_zP1 montante S1 , -k_zS1 évanescente P2 , k_zP2 = iω(p²V_P2²-1)^½/V_P2 évanescente S2 , k_zS2 = iω(p²V_S2²-1)^½/V_S2
z = -H σ_zz(k_zP1²)Z_P1 -2μ₁k_xk_zS1Z_S1 σ_zz(k_zP1²)/Z_P1 2μ₁k_xk_zS1/Z_S1 0 0
-2μ₁k_xk_zP1Z_P1 σ_zx(k_zS1²)Z_S1 2μ₁k_xk_zP1/Z_P1 σ_zx(k_zS1²)/Z_S1 0 0
z = 0 k_x -k_zS1 k_x k_zS1 -k_x k_zS2
k_zP1 k_x -k_zP1 k_x -k_zP2 -k_x
σ_zz(k_zP1²) -2μ₁k_xk_zS1 σ_zz(k_zP1²) 2μ₁k_xk_zS1 -σ_zz(k_zP2²) 2μ₂k_xk_zS2
-2μ₁k_xk_zP1 σ_zx(k_zS1²) 2μ₁k_xk_zP1 σ_zx(k_zS1²) 2μ₂k_xk_zP2 -σ_zx(k_zS2²)

La partie haute fréquence de la courbe de dispersion du mode fondamental (V_RS1≤V_R0≤V_S1) correspond à l'onde de Rayleigh guidée par la surface libre de la couche couplée à une onde de Stoneley guidée par l'interface (ou deux ondes P et SV évanescentes dans la couche depuis la surface couplées à quatre ondes évanescentes depuis l'interface). A haute fréquence, V_R0 = V_RS1 (l'onde de longueur d'onde << H ne voit que la couche).

cond. lim. ondes guidées par surf.libre en z = -H et prolongées en z = 0 par
Z_P1 = e^{-ω(p²V_P1²-1)^½/V_P1H} (0) ; Z_S1 = e^{-ω(p²V_S1²-1)^½/V_S1H} (0) ondes guidées par interf. en z = 0 et prolongées en z = -H par Z_P1 , Z_S1
z = -H Rayleigh surf. libre (1-2p²V_S1²)Z_P1 (0) -i2pV_S1(p²V_S1²-1)^½Z_S1 (0) 0 0
+i2V_S1²p(p²V_P1²-1)^½/V_P1Z_P1 (0) +(1-2p²V_S1²)Z_S1 (0) 0 0
z = 0 pZ_P1 (0) -i(p²V_S1²-1)^½/V_S1Z_S1 (0) Stoneley à l'interface
i(p²V_P1²-1)^½/V_P1Z_P1 (0) pZ_S1 (0)
ρ₁(1-2p²V_S1²)Z_P1 (0) i2ρ₁V_S1²p(p²V_S1²-1)^½/V_S1Z_S1 (0)
-i2ρ₁V_S1²p(p²V_P1²-1)^½/V_P1Z_P1 (0) ρ₁(1-2p²V_S1²)Z_S1 (0)

FU C.Y. (1946) : STUDIES ON SEISMIC WAVES: II. RAYLEIGH WAVES IN A SUPERFICIAL LAYER

Vitesse de groupe

En présence de dispersion, chaque fréquence se propage à une vitesse différente. Pour un signal comportant plusieurs fréquences, la somme des sinusoïdes qui le constituent produit des interférences constructives et destructives. Les interférences constructives produisent le groupe d'onde qui se propage à la vitesse de groupe, elle-même fonction de la fréquence.

superposition d'ondes harmoniques de vitesses de phase V(ω)=ω/k interférence constructive en (x,t) ⇔ phase stationnaire pour ondes harmoniques (la variation de U est négligeable) ⇒ vitesse de groupe V_g
u(x,t) = ∫U(ω)e^{iω(x/V(ω)-t)}dω = ∫U(ω)e^{i(k(ω)x-ωt)}dω = ∫U(k)e^i(kx-ω(k)t)dk d(k(ω)x-ωt)/dω = (dk/dω)x-t = 0 ⇒ V_g = dω/dk = V+kdV/dk = 1/(dk/dω) = 1/(p+ωdp/dω)
-
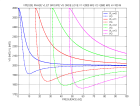légende lovg - displov.m
relation de dispersion de l'onde de Love : tg(Hω(p_n)(1-p_n²V_S1²)^½/V_S1) = (ρ₂V_S2(p²V_S2²-1)^½)/(ρ₁V_S1(1-p²V_S1²)^½)
dérivation de la relation de dispersion :
(H/V_S1)((1-p_n²V_S1²)^½-ωp_nV_S1²(1-p_n²V_S1²)^-½dp_n/dω)/cos²(Hω(1-p_n²V_S1²)^½/V_S1)) = (ρ₂V_S2)/(ρ₁V_S1)(1-p_n²V_S1²)^-½(p_nV_S2²(p_n²V_S2²-1)^-½+p_nV_S1²(p_n²V_S2²-1)^½/(1-p_n²V_S1²))dp_n/dω
dp_n/dω = (H/V_S1)(1-p_n²V_S1²)/
(Hωp_nV_S1+(ρ₂V_S2)/(ρ₁V_S1)cos²(Hω(1-p_n²V_S1²)^½/V_S1)(p_nV_S2²(p_n²V_S2²-1)^-½+p_nV_S1²(p_n²V_S2²-1)^½/(1-p_n²V_S1²)))

Kelly K.R. , 1983, Numerical study of Love wave propagation construit des sismogrammes synthétiques par superposition d'ondes de Love dans une couche et illustre l'effet des variations latérales de vitesses.
Roth M. and K. Holliger, 1999, Inversion of source-generated noise in high-resolution seismic data montrent l'effet de la dispersion des ondes guidées dans une couche de faible épaisseur.

Onde de Love guidée en milieu stratifié

Pour les basses fréquences où l'onde de Love est stationnaire dans les couches et évanescente deans le demi-espace, les relations de dispersion s'obtiennent en empilant les couches d'épaisseur h_i au dessus de l'interface avec le demi-espace z > 0 où se produit la réflexion totale avec un déphasage χ. Dans chaque couche les ondes harmoniques montante et descendante sont prolongées vers le haut par un déphasage vertical ±k_izh_i. Si la face supérieure de la couche est la surface libre, la condition de réflexion totale donne la relation de dispersion de l'onde de Love. Si la face supérieure de la couche est une interface avec une couche au dessus, les conditions de continuité sur le déplacement u_y et la contrainte σ_yz donnent les amplitudes des ondes montantes et descendantes dans la couche supérieure (le tableau se lit de bas en haut).

Pour les hautes fréquences, l'onde peut être soit stationnaire, soit évanescente dans les couches en sandwich entre la couche supérieure et le demi-espace. Les relations de dispersion s'obtiennent en exprimant les relations entre ondes montantes et descendantes dans une stratication. Le cas pour deux couches est donné sur la partie droite du tableau. Les ondes montantes et descendantes à la surface libre ont une amplitude égale à 1. Elles sont prolongées à la base de la couche 2 (k_2z est réel). L'onde descendante à la base de la couche 1 est la somme de l'onde descendante venant de la couche du-dessus transmise à travers l'interface 21, propagée dans la couche 1 (si k_1z est réel) ou d'amplitude diminuée (si k_1z est imaginaire) et de l'onde montante à la base de la couche 1 propagée ou atténuée dans la couche 1 (aller-retour) et réfléchie sur l'interface 12. L'onde montante à la base de la couche 2 est la somme de l'onde descendante à la base de la couche 2 réfléchie par l'interface 21 et de l'onde montante à la base de la couche 1, propagée ou atténuée dans la couche 1 et transmise à travers l'interface 12. Le rapport onde montante sur onde descendante à la base de la couche 1 est le coefficient de réflexion sur l'interface 10.

z
I_i = ρ_iV_Si²k_iz onde descendante e^k_izz
k_iz = ω(1/V_Si²-p²)^½ onde montante e^-ik_izz continuité u_y et σ_yz à l'interface
réflexion totale si surface libre (montante = descendante)
relation de dispersion basse fréquence onde descendante e^k_izz
R₂₁ = (I₂-I₁)/(I₂+I₁)
T₂₁ = 2I₂/(I₂+I₁) onde montante e^-ik_izz
T₁₂ = 2I₁/(I₂+I₁)
R₁₂ = -R₂₁ T₂₁ = 1+R₂₁
T₁₂ = 1+R₁₂ = 1-R₂₁
T₁₂T₂₁-R₁₂R₂₁ = 1
-(h₃+h₂+h₁)
couche 3 D₃e^-ik_3zh₃ = D₃(a₃-ib₃) M₃e^ik_3zh₃ = M₃(a₃+ib₃) A₃b₃+a₃B₃ = 0
tg(k_3zh₃)+(I₂/I₃)tg(k_2zh₂)+((I₁/I₃)-(I₁/I₂)tg(k_3zh₃)tg(k_2zh₂))tg(k_1zh₁+χ/2) = 0
-(h₂+h₁)
couche 3 D₃ = A₃-iB₃ M₃ = A₃+iB₃ A₃ = A₂a₂-B₂b₂ = a₁a₂-(I₁/I₂)b₁b₂
B₃ = (I₂/I₃)(A₂b₂+B₂a₂) = (I₂/I₃)a₁b₂+(I₁/I₃)b₁a₂
-(h₂+h₁)
couche 2 D₂e^-ik_2zh₂ = D₂(a₂-ib₂) M₂e^ik_2zh₂ = M₂(a₂+ib₂) A₂b₂+a₂B₂ = 0
tg(k_2zh₂)+(I₁/I₂)tg(k_1zh₁+χ/2) = 0 1 1 (1-R₁₀R₁₂e^i2k_1zh₁)(1 - R₂₁e^i2k_2zh₂) = T₁₂ R₁₀T₂₁e^{i2(k_2zh₂+k_1zh₁)}
(e^-i2k_1zh₁-R₁₀R₁₂)(e^-i2k_2zh₂ - R₂₁) = T₁₂ R₁₀T₂₁
e^{-i2(k_2zh₂+k_1zh₁)}+R₂₁(R₁₀e^-i2k_2zh₂-e^-i2k_1zh₁) = R₁₀
-h₁
couche 2 D₂ = A₂-iB₂ M₂ = A₂+iB₂ A₂ = a₁
B₂ = (I₁/I₂)b₁ e^ik_2zh₂ e^-ik_2zh₂ = R₂₁e^ik_2zh₂+T₁₂Me^ik_1zh₁ M = (e^-ik_2zh₂ - R₂₁e^ik_2zh₂)e^-ik_1zh₁/T₁₂
-h₁
couche 1 D₁e^-ik_1zh₁ = a₁-ib₁ M₁e^ik_1zh₁ = a₁+ib₁ b₁ = 0
sin(k_1zh₁+χ/2) = 0 onde stationnaire si k_1z réel, évanescente si k_1z imaginaire
0
couche 1 D₁ = e^-iχ/2 M₁ = e^iχ/2 χ(p) = -2Arctg(ρV_S(p²V_S²-1)^½/ρ₁V_S1(1-p²V_S1²)^½) = -2Arctg(I/I₁) D = T₂₁e^{i(k_2zh₂+k_1zh₁})+R₁₂Me^i2k_1zh₁ M = R₁₀D = (I₁-I₀)D/(I₁+I₀) M = R₁₀T₂₁e^{i(k_2zh₂+k_1zh₁})/(1-R₁₀R₁₂e^i2k_1zh₁)
> 0
1/2 espace onde évanescente e^-k_zz
k_z = |ω|(p²-1/V²)^½ onde évanescente e^-k_zz
k_z = |ω|(p²-1/V²)^½

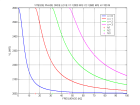
Voici la courbe de dispersion pour une onde de Love dans un milieu comportant deux couches sur un demi-espace.
La détermination des fréquences du monde fondamental et des harmoniques pour la partie de la courbe correspondant à une onde stationnaire dans les couches et évanescente dans le demi-espace (partie basse fréquence de la courbe de dispersion) est illustrée sur cette figure.
A plus haute fréquence, l'onde devient évanescente dans la couche intermédiaire. La détermination des fréquences dans ce cas est illustrée sur cette figure.
La courbe de dispersion à haute-fréquence est asymptotique à celle de l'onde de Love dans la couche supérieure sur le demi-espace de vitesse égale à celle de la couche intermédiaire : l'onde ne voit pas le milieu inférieur car l'amplitude y est négligeable.

Voici l'amplitude du déplacement pour une vitesse V_L telle que l'onde est stationnaire dans les couches et évanescente dans le demi-espace.

Ondes cylindriques

Pour une symétrie cylindrique, les solutions harmoniques de l'équation des ondes font intervenir les fonctions de Bessel et Hankel d'ordre n = 0,1,2... où n correspond à la variation azimutale e^inθ.
Pour k_rr>>1, elles sont similaires à des sinusoïdes d'amplitude décroissant comme (1/r)^½ :

eq. de Bessel solution dérivation
r²d²f/dr²+rdf/dr+ (k_r²r²-n²)f(r) = 0 f(r) = H_n(k_rr) = J_n(k_rr)+iY_n(k_rr) ≈ (2/πk_rr)^½e^{i(k_rr-π/4-nπ/2)}
H_n(ik_rr) ≈ i^-(n+1)(2/πk_rr)^½e^-k_rr
dH_n(k_rr)/dr = k_rH_n-1(k_rr)-(n/r)H_n(k_rr) = (n/r)H_n(k_rr)-k_rH_n+1(k_rr)

En l'absence de variation azimutale, les potentiels de déplacement des ondes P et S sont :

Δφ(r,z) = ∂²φ/∂r²+(1/r)∂φ/∂r+∂²φ/∂z² = (1/V_P²)∂²φ/∂t² φ(r,z) = f(r)e^i(k_zz-ωt) k_p² = ω²/V_P²-k_z² f(r) = AH₀(k_pr)
Δψ_θ(r,z) = (1/V_S²)∂²ψ_θ/∂t² ψ_θ(r,z) = g(r)e^i(k_zz-ωt) k_s² = ω²/V_S²-k_z² g(r) = BH₁(k_sr)

Dans le cas où il y a une variation angulaire avec θ, on a :

Δφ(r,θ,z) = Δφ(r,z) + (1/r)²∂²φ/∂θ² = (1/V_P²)∂²φ/∂t² φ(r,θ,z) =f(r)cos(nθ)e^i(k_zz-ωt) k_p² = ω²/V_P²-k_z² f(r) = AH_n(k_pr)
Δψ_r(r,θ,z) = (1/V_S²)∂²ψ_r/∂t² ψ_r(r,z) = g(r)sin(nθ)e^i(k_zz-ωt) k_s² = ω²/V_S²-k_z² g(r) = BH_n+1(k_sr)
Δψ_θ(r,θ,z) = (1/V_S²)∂²ψ_θ/∂t² ψ_θ(r,z) = -g(r)cos(nθ)e^i(k_zz-ωt)
Δψ_z(r,θ,z) = (1/V_S²)∂²ψ_z/∂t² ψ_z(r,z) = h(r)sin(nθ)e^i(k_zz-ωt) h(r) = CH_n(k_sr)

Déplacements et déformations sur la paroi d'un forage :

u_r = cos(nθ) u_θ = sin(nθ) u_z = cos(nθ) ε_rr = cos(nθ) ε_rθ = sin(nθ) ε_rz = cos(nθ)
Ae^i(k_zz-ωt) n/rH_n(k_pr)-k_pH_n+1(k_pr) -n/rH_n(k_pr) ik_zH_n(k_pr) (n(n-1)/r²-k_p²)H_n(k_pr)+k_p/rH_n+1(k_pr) -n(n-0.5)/r²H_n(k_pr)+nk_p/rH_n+1(k_pr) ik_z(n/rH_n(k_pr)-k_pH_n+1(k_pr))
Be^i(k_zz-ωt) ik_zH_n+1(k_sr) ik_zH_n+1(k_sr) -k_sH_n(k_sr) ik_z(k_sH_n(k_sr)-(n+1)/rH_n+1(k_sr)) ik_z(k_s/2H_n(k_sr)-(n+1)/rH_n+1(k_sr)) (-nk_s/rH_n(k_sr)+(k_s²-k_z²)H_n+1(k_sr))/2
Ce^i(k_zz-ωt) n/rH_n(k_sr) -n/rH_n(k_sr)+k_sH_n+1(k_sr) 0 n(n-1)/r²H_n(k_sr)-nk_s/rH_n+1(k_sr) (-n(n-1)/r²+k_s²/2)H_n(k_sr)-k_s/rH_n+1(k_sr) (ik_zn/2r)H_n(k_sr)

Les solutions P et S en coordonnées cylindriques sont développées en détail dans : Sinha, B.K., E. Simsek, and S. Asvadurov, 2009 Influence of a pipe tool on borehole modes

Ondes P et S dues à une force ponctuelle

En l'absence de forces de volume, les 3 équations d'équilibre élastiques écrites en termes des composantes du déplacement des particules s'écrivent :
ρ∂²u/∂t² = (λ+μ)graddivu+μΔu où Δu = (Δu_x, Δu_y, Δu_z) = grad(divu)-rot(rot(u))

On obtient l'équation des ondes P, ∂²φ/∂t² = V_P²Δφ, à partir de ces 3 équations en posant u = gradφ. En effet Δgradφ = gradΔφ car rot(gradφ) = 0. Donc ρgrad∂²φ/∂t² = (λ+2μ)grad(Δφ).
On obtient l'équation des ondes S, ∂²ψ/∂t² = V_S²Δψ, en posant u = rotψ avec divψ = 0. En effet Δrotψ = -rotrotrotψ = rotΔψ car divrotψ = 0 et divψ = 0. Donc ρrot∂²ψ/∂t² = μrotΔψ.

Pour une source ponctuelle due à une force de module F(t) orientée dans une direction e, la force par unité de volume s'écrit :
f = F(t)eδ(x) = -F(t)/(4π)eΔ(1/r) = -F(t)/(4π)Δ(e/r) = -(F(t)/(4π))(graddiv(e/r)-rotrot(e/r)).
En effet, ∫δ(x)dx = 1 et ∫Δ(1/r)dx = ∫grad(1/r).dS = (-1/r²)e_r.4πr²e_r = -4π impliquent δ(x) = -1/(4π)Δ(1/r). Comme e est constant, eΔ(1/r) = Δ(e/r).
On considère le cas harmonique du à une force oscillant sinusoïdalement avec une pulsation ω : F(t) = Fe^-iωt.

θ étant l'angle entre la direction e d'application de la force et la direction radiale e_r de propagation de l'onde depuis le point d'application de la force, on a e = cosθe_r-sinθe_θ.
On utilise l'expression des opérateurs différentiels en coordonnées sphériques (r,θ,ξ) : gradφ(r,θ) = ∂φ/∂re_r+1/r∂φ/∂θe_θ et rot(ψ(r,θ)e_ξ) = (1/r)(1/sinθ∂(sinθψ)/∂θe_r-∂(rψ)/∂re_θ).

Les équations d'équilibre avec la partie du terme source générant les ondes P s'écrivent ρgrad∂²φ/∂t² = (λ+2μ)grad(Δφ)-(F(t)/(4π)(graddiv(e/r)
L'équation des ondes P devient ∂²φ/∂t² = V_P²Δφ-(F(t)/4πρ)div(e/r). Elle comporte un terme source proportionnel à (dive/r) = grad(1/r).e = -1/r²e_r.e = -cosθ/r²
L'amplitude du potentiel de déplacement des particules et du déplacement en champ lointain est ainsi proportionnelle à cosθ.
En écrivant le potentiel du déplacement des particules sous la forme de la divergence d'un vecteur Φ(r)e, on sépare les dépendances en r et θ.

u = gradφ(r,θ) ∂²φ/∂t² = V_P²Δφ-(F(t)/4πρ)div(e/r) φ(r,θ) = div(Φ(r)e) ∂²Φ/∂t² = V_P²ΔΦ-F(t)/(4πρr) ∂²(rΦ)/∂t² = V_P²∂²(rΦ)/∂r²-F(t)/(4πρ)
F(t) = Fe^-iωt, k = ω/V_P ∂²(rΦ)/∂r²+k²(rΦ) = F/(4πρV_P²) Φ = F/(4πρV_P²k²)(1-e^ikr)/r φ = gradΦ(r).e = cosθ∂Φ/∂r = -Fcosθ/(4πρV_P²k²)((ik-1/r)e^ikr/r+1/r²)
u = cosθ∂²Φ/∂r²e_r-1/r∂Φ/∂rsinθe_θ = cosθ∂²Φ/∂r²e_r+1/r∂Φ/∂r(e-cosθe_r)
u = ( -F/(4πρV_P²k²)) ((cosθ(2/r²-2ik/r-k²)e_r+1/r(ik-1/r)(e-cosθe_r))e^ikr/r) -(1/r³)(3cosθe_r-e)) u_cl = Fcosθe_r/(4πρV_P²)e^ikr/r u_cp = -F/(4πρV_P²)(e-3cosθe_r)((i/kr-1/(kr)²)e^ikr/r+1/r³)

Les équations d'équilibre avec la partie du terme source générant les ondes S s'écrivent ρrot∂²ψ/∂t² = μrotΔψ+(F(t)/(4π))rotrot(e/r).
L'équation des ondes S devient ∂²ψ/∂t² =V_S²Δψ+(F(t)/(4πρ))rot(e/r). Elle comporte un terme source proportionnel à rot(e/r) = grad(1/r)∧e = -(1/r²)e_r∧e = sinθe_ξ/r²
L'amplitude du potentiel de déplacement des particules et du déplacement en champ lointain est ainsi proportionnelle à sinθ.
En écrivant le potentiel du déplacement des particules sous la forme du rotationnel d'un vecteur Ψ(r)e, on sépare les dépendances en r et θ.

u = rotψ(r,θ) ∂²ψ/∂t² = V_S²Δψ+(F(t)/4πρ)rot(e/r) ψ(r,θ) = -rot(Ψ(r)e) ∂²Ψ/∂t² = V_S²ΔΨ-F(t)/(4πρr) ∂²(rΨ)/∂t² = V_S²∂²(rΨ)/∂r²-F(t)/(4πρ)
F(t) = Fe^-iωt, k = ω/V_S ∂²(rΨ)/∂r²+k²(rΨ) = F/(4πρV_S²) Ψ = F/(4πρV_S²k²)(1-e^ikr)/r ψ(r,θ) = -gradΨ(r)∧e = sinθ∂Ψ/∂re_ξ = -Fsinθe_ξ/(4πρV_S²k²)((ik-1/r)e^ikr/r+1/r²)
u = (1/r)(2cosθe_r∂Ψ/∂r-sinθe_θ∂(r∂Ψ/∂r)/∂r) = (1/r)(2(e+sinθe_θ)∂Ψ/∂r-sinθe_θ(∂Ψ/∂r+r∂²Ψ/∂r²))
u = -F/(4πρV_S²k²) (1/r)((2(e+sinθe_θ)(ik-1/r)-sinθe_θ(-rk²-ik+1/r))e^ikr/r +(1/r²)(2e+3sinθe_θ)) u_cl = -Fsinθe_θ/(4πρV_S²)e^ikr/r u_cp = F/(4πρV_S²)(e-3cosθe_r) ((i/kr-1/(kr)²)e^ikr/r+1/r³)

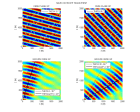
Voici comment les termes de déplacement en champ proche et lointains contribuent au déplacement des particules et à la polarisation des ondes P et S aux distances de la source voisines de la longueur d'onde :
- - -
force.m

Anisotropie (cas isotrope transverse) : milieu équivalent - propagation

Lorsque le milieu de propagation n'est pas isotrope, les caractéristiques des ondes sismiques sont plus complexes : les vitesses de propagation dépendent de la direction de propagation, les polarisations des ondes ne sont plus parfaitement longitudinales ou transverses, les vitesses des ondes SH et SV ne sont plus égales (biréfringence).
Un milieu stratifié horizontalement composé de couches isotropes fines devant la longueur d'onde a un comportement anisotrope du type millefeuilles : si on le comprime verticalement, les couches élastiques sont en série ; si on le comprime horizontalement, les couches élastiques sont en parallèle. Un tel milieu composite peut être remplacé par un milieu équivalent homogène au comportement anisotrope caractérisé par une isotropie transverse. Les relations contrainte-déformation font intervenir cinq coefficients élastiques au lieu de deux pour le milieu isotrope.
Pour établir les coefficients élastiques anisotropes équivalents dans ce cas, on considère des états de contrainte-déformation qui permettent de calculer un coefficient anisotrope à partir de moyennes des coefficients isotropes.

cas isotrope : 2 coef. élastiques λ et μ isotropie transverse (axe principal Oz) : 5 coef. élastiques exemple pour des argiles (x10⁹Pa)
σ_xx = c₁₁ε_xx+c₁₂ε_yy+c₁₂ε_zz
σ_xy = (c₁₁-c₁₂)ε_xy
c₁₁ = λ+2μ , c₁₂ = λ σ_xx = c₁₁ε_xx+c₁₂ε_yy+c₁₃ε_zz , σ_yy = c₁₂ε_xx+c₁₁ε_yy+c₁₃ε_zz
σ_zz = c₁₃ε_xx+c₁₃ε_yy+c₃₃ε_zz
σ_yz = 2c₄₄ε_yz , σ_zx = 2c₄₄ε_zx
σ_xy = 2c₆₆ε_xy , c₆₆ = (c₁₁-c₁₂)/2 c₁₁ = 45 , c₁₂ = 10 , c₁₃ = 8
c₃₃ = 28
c₄₄ = 11
c₆₆ = (c₁₁-c₁₂)/2 = 17.5

σ , ε appliquées sur milieu finement stratifié d'épaisseur H couches horizontales d'épaisseur h_i, p_i = h_i/H modules anisotropes équivalents
couches comprimées en série verticalement : σ_zz ≠ 0
sans déformation latérale : ε_xx = ε_yy = 0 σ_zzi = σ_zz , ε_zzi = σ_zz/(λ_i+2μ_i)
ε_zz = ∑p_iε_zzi = σ_zz∑p_i/(λ_i+2μ_i)
σ_xxi = σ_yyi = λ_iε_zzi σ_zz = c₃₃ε_zz
c₃₃ = 1/∑p_i/(λ_i+2μ_i)
couches comprimées en parallèle horizontalement selon x : σ_xx ≠ 0
sans déformation selon y : ε_yy = 0
sans déformation verticale moyenne : ε_zz = ∑p_iε_zzi = 0
déformation selon x uniforme : ε_xxi = ε_xx σ_xxi = (λ_i+2μ_i)ε_xx+λ_iε_zzi
σ_xx = ∑p_iσ_xxi = ε_xx∑p_i(λ_i+2μ_i)+∑p_iλ_iε_zzi [1]
σ_zzi = σ_zz , σ_zz = λ_iε_xx+(λ_i+2μ_i)ε_zzi [2]
[2] ⇒ σ_zz∑p_i/(λ_i+2μ_i) = ε_xx∑p_iλ_i/(λ_i+2μ_i) + ∑p_iε_zzi = ε_xx∑p_iλ_i/(λ_i+2μ_i) [3]
[2,3] ⇒ ∑p_iλ_iε_zzi = ε_xx((∑p_iλ_i/(λ_i+2μ_i))²/∑p_i/(λ_i+2μ_i)-∑p_iλ_i²/(λ_i+2μ_i)) [4] σ_xx = c₁₁ε_xx
[1,4] ⇒ c₁₁ = c₃₃(∑p_iλ_i/(λ_i+2μ_i))²+4∑p_iμ_i(λ_i+μ_i)/(λ_i+2μ_i)
couches cisaillées en série horizontalement : σ_yz ≠ 0 σ_yz = 2μ_iε_yzi
ε_yz = ∑p_iε_yzi = (σ_yz/2)∑p_i/μ_i σ_yz = 2c₄₄ε_yz
c₄₄ = 1/∑p_i/μ_i
couches cisaillées en parallèle horizontalement : σ_xy ≠ 0
déformation uniforme : ε_xyi = ε_xy σ_xyi = 2μ_iε_xy
σ_xy = ∑p_iσ_xyi = 2∑p_iμ_iε_xy σ_xy = 2c₆₆ε_xy
c₆₆ = ∑p_iμ_i , c₁₂ = c₁₁-2c₆₆
couches comprimées en parallèle horizontalement selon x : σ_xx ≠ 0
sans contrainte verticale : σ_zz = 0
sans déformation selon y : ε_yy = 0
déformation selon x uniforme : ε_xxi = ε_xx σ_xxi = (λ_i+2μ_i)ε_xx+λ_iε_zzi
σ_zzi = σ_zz = 0 , λ_iε_xx+(λ_i+2μ_i)ε_zzi = 0
ε_zz = ∑p_iε_zzi = -ε_xx∑p_iλ_i/(λ_i+2μ_i) σ_zz = c₁₃ε_xx+c₃₃ε_zz = 0
c₁₃ = c₃₃(∑p_iλ_i/(λ_i+2μ_i))

Voici l'illustration de ces différents états de déformations et contraintes et les modules anisotropes équivalents obtenus pour une stratification alternant en proportion égale des couches sédimentaires rapides et lentes :

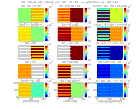
anisomod.m

ondes planes SH (polarisation horizontale) ondes planes quasi-P (polarisation α quasi-longitudinale : α ≈ θ)
ondes planes quasi-SV (polarisation β quasi-transverse : β ≈ η-π/2)
u_y(x,z,t) = U_ye^{i(k_xx+k_zz-ωt)}
ρω² = (c₆₆k_x²+c₄₄k_z²)
la relation de dispersion est une ellipse de demi-axes (c₆₆/ρ)^-½ et (c₄₄/ρ)^-½ u(x,z,t) = (U_x,0,U_z)e^{i(k_xx+k_zz-ωt)}
ρω²U_x = (c₁₁k_x²+c₄₄k_z²)U_x+(c₁₃+c₄₄)k_xk_zU_z
ρω²U_z = (c₁₃+c₄₄)k_xk_zU_x+(c₄₄k_x²+c₃₃k_z²)U_z
(ρω²-c₁₁k_x²-c₄₄k_z²)(ρω²-c₄₄k_x²-c₃₃k_z²)-((c₁₃+c₄₄)k_xk_z)² = 0
V_SH² = (1/ρ)(c₆₆sin²η+c₄₄cos²η) V_QP² = (1/2ρ)(c₄₄+c₁₁sin²θ+c₃₃cos²θ+D)
V_QS² = (1/2ρ)(c₄₄+c₁₁sin²θ+c₃₃cos²θ-D)
D² = ((c₁₁-c₄₄)sin²θ-(c₃₃-c₄₄)cos²θ)²+(c₁₃+c₄₄)²sin²2θ
tgα = U_x/U_z = (c₁₃+c₄₄)sin2θ/2(ρV_QP²-c₁₁sin²θ-c₄₄cos²θ) = (c₁₃+c₄₄)sin2θ/((c₄₄-c₁₁)sin²θ+(c₃₃-c₄₄)cos²θ+D)
tgβ = U_x/U_z = (c₁₃+c₄₄)sin2θ/2(ρV_QS²-c₁₁sin²θ-c₄₄cos²θ) = (c₁₃+c₄₄)sin2θ/((c₄₄-c₁₁)sin²θ+(c₃₃-c₄₄)cos²θ-D)
tgα.tgβ = ((c₁₃+c₄₄)sin2θ)²/(((c₄₄-c₁₁)sin²θ+(c₃₃-c₄₄)cos²θ)²-D²) = -1 ⇒ β = α-π/2
vitesse de groupe ⇔ phase stationnaire dans ∫∫U(k_x,k_z)e^{i(k_xx+k_zz-ω(k_x,k_z)t)}dk_xdk_z pour avoir interférence constructive des ondes harmoniques en (x,z,t)
∂(k_xx+k_zz-ω(k_x,k_z)t)/∂k_x = 0 , x-(∂ω/∂k_x)t = 0 , V_Gx = ∂ω/∂k_x
∂(k_xx+k_zz-ω(k_x,k_z)t)/∂k_z = 0 , z-(∂ω/∂k_z)t = 0 , V_Gz = ∂ω/∂k_z
V_G = grad_kω(k_x,k_z) ⇒ e_k.V_G = e_k.grad_kω(k_x,k_z) = dω/dk = V_phase ⇒ V_G ≥ V_phase
V_Gx = (c₆₆/ρω)k_x , V_Gz = (c₄₄/ρω)k_z
V_G² = (1/ρ²ω²)((c₆₆k_x)²+(c₄₄k_z)²)
sinη_g = V_Gx/V_G = (c₆₆k_x)/((c₆₆k_x)²+(c₄₄k_z)²)^½
cosη_g = V_Gz/V_G = (c₄₄k_z)/((c₆₆k_x)²+(c₄₄k_z)²)^½
V_G² = 1/(ρ(sin²η_g/c₆₆+cos²η_g/c₄₄)) V_Gx = ∂(kV)/∂k_x = V∂k/∂k_x+k∂V/∂k_x
k = (k_x²+k_z²)^½ , ∂k/∂k_x = k_x/k = sinθ
k_x = ksinθ , 1 = ∂k/∂k_xsinθ+kcosθ∂θ/∂k_x , ∂θ/∂k_x = cosθ/k
V_Gx = Vsinθ+cosθdV/dθ , V_Gz = Vcosθ-sinθdV/dθ
V_G² = V²+(dV/dθ)²
tgθ_g = V_Gx/V_Gz = (tgθ+(1/V)dV/dθ)/(1-(tgθ/V)dV/dθ)
paramètres d'anisotropie de Thomsen utilisés dans le traitement des données de sismique réflexion : α_T , β_T , γ_T , δ_T , ε_T
η = 0 , V_SH² = c₄₄/ρ = β_T² , η = 90° , V_SH² = c₆₆/ρ
γ_T = (V_SH²(90)-V_SH²(0))/2V_SH²(0) = (c₆₆-c₄₄)/2c₄₄
V_SH² = β_T²((c₆₆/c₄₄)sin²η+cos²η) = β_T²(1+2γ_Tsin²η)
V_G² = β_T²((1+2γ_T)/(1+2γ_Tcos²η_g)) θ = 0 , D = (c₃₃-c₄₄) , V_QP² = c₃₃/ρ = α_T² , V_QS² = c₄₄/ρ = β_T²
θ = 90° , D = (c₁₁-c₄₄) , V_QP² = c₁₁/ρ , V_QS² = c₄₄/ρ = β_T²
ε_T = (V_QP²(90)-V_QP²(0))/2V_QP²(0) = (c₁₁-c₃₃)/2c₃₃
δ_T = (1/2α_T)(d²V_QP/dθ²)(0) = ((c₁₃+c₄₄)²-(c₃₃-c₄₄)²)/(2c₃₃(c₃₃-c₄₄))
pour l'exemple des argiles (ρ=2380 kg/m³) : α_T = 3.43 km/s, β_T = 2.15 km/s , γ_T = 0.3 , δ_T = 0.07 , ε_T = 0.3
faible anisotropie
γ_T<<1 , γ_T ≈ (V_SH(90)-V_SH(0))/V_SH(0)
V_SH ≈ β_T(1+γ_Tsin²η) ε_T<<1 , δ_T<<1 , ε_T ≈ (V_QP(90)-V_QP(0))/V_QP(0)
V_QP ≈ α_T(1+δ_Tsin²θcos²θ+ε_Tsin⁴θ) = α_T(1+δ_Tsin²θ+(ε_T-δ_T)sin⁴θ)
V_QS ≈ β_T(1+(α_T²/β_T²)(ε_T-δ_T)sin²θcos²θ)

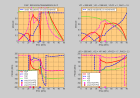
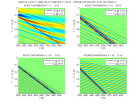
Voici les vitesses de phase et de groupe et les polarisations obtenues avec les valeurs du tableau ci-dessus, ainsi que les groupes d'ondes SH et QP pour différents éventails d'angle de phase :
- -
légende anisopro - anisopro.m

Pour le calcul des coefficients de réflexion-transmission QP-QSV, on écrit les composantes du déplacement des particules en fonction de l'angle de polarisation α pour les ondes QP et de l'angle β = angle de polarisation QSV + π/2 pour les ondes QS (comme dans le cas isotrope). La loi de Snell s'applique toujours mais ne donne pas explicitement les différents angles d'incidence puisque les vitesses dépendent de ces angles. La relation de dispersion permet d'obtenir les angles θ(p) et η(p), ou plus généralement k_z^P = ωq^P(p) et k_z^S = ωq^S(p), imaginaires pour les ondes évanescentes.

Loi de Snell : p = sinθ₁/V_QP1(θ₁) = sinθ₂/V_QP2(θ₂) = sinη₁/V_QS1(η₁) = sinη₂/V_QS2(η₂) ;
q^P1(p) = (cosθ₁/V_QP1)(p) ; q^P2(p) = (cosθ₂/V_QP2)(p) ; q^S1(p) = (cosη₁/V_QS1)(p) ; q^S2(p) = (cosη₁/V_QS2)(p) ;
Relation de dispersion : (ρ-c₁₁p²-c₄₄q²)(ρ-c₄₄p²-c₃₃q²)-((c₁₃+c₄₄)pq)² = 0
Aq⁴+Bq²+C = 0 ; A = c₃₃c₄₄ ; B = -c₃₃(ρ-c₁₁p²)-c₄₄(ρ-c₄₄p²)-(c₁₃+c₄₄)²p² ; C = (ρ-c₁₁p²)(ρ-c₄₄p²) ; Δ = (B²-4AC)^½
q^P = ((-B-Δ)/2A)^½ ; q^S = ((-B+Δ)/2A)^½ ;
Polarisation : α = Arctg((c₁₃+c₄₄)pq^P/(ρ-c₁₁p²-c₄₄(q^P)²)) ; β = π/2+Arctg((c₁₃+c₄₄)pq^S/(ρ-c₁₁p²-c₄₄(q^S)²))
QP incidente descendante + réfléchie montante
U^I = (sinα₁,cosα₁) , U^RP = R_P(sinα₁,-cosα₁)
k_z^I = ωq^P1(p) , k_z^RP = -ωq^P1(p) QSV réfléchie montante
U^RS = R_S(cosβ₁,sinβ₁)
k_z^RS = -ωq^S1(p) QP transmise descendante
U^TP = T_P(sinα₂,cosα₂)
k_z^TP = ωq^P2(p) QSV transmise descendante
U^TS = T_S(-cosβ₂,sinβ₂)
k_z^TS = ωq^S2(p)
U_x = sinα₁(1+R_P) + cosβ₁R_S = sinα₂T_P -cosβ₂T_S
U_z = cosα₁(1-R_P) + sinβ₁R_S = cosα₂T_P + sinβ₂T_S
Σ_zz = (c₁₃sinα₁p+c₃₃cosα₁q^P1)(1+R_P) + (c₁₃cosβ₁p-c₃₃sinβ₁q^S1)R_S = (d₁₃sinα₂p+d₃₃cosα₂q^P2)T_P + (-d₁₃cosβ₂p+d₃₃sinβ₂q^S2)T_S
Σ_zx = c₄₄(sinα₁q^P1+cosα₁p)(1-R_P) + c₄₄(-cosβ₁q^S1+sinβ₁p)R_S = d₄₄(sinα₂q^P2+cosα₂p)T_P + d₄₄(-cosβ₂q^S2+sinβ₂p)T_S
écriture matricielle : AR = B ; R = [R_P , R_S , T_P , T_S]^t ; B = [-sinα₁ , -cosα₁ , -(c₁₃sinα₁p+c₃₃cosα₁q^P1) , c₄₄(sinα₁q^P1+cosα₁p)]^t
A sinα₁ cosβ₁ -sinα₂ cosβ₂
-cosα₁ sinβ₁ -cosα₂ -sinβ₂
(c₁₃sinα₁p+c₃₃cosα₁q^P1) (c₁₃cosβ₁p-c₃₃sinβ₁q^S1) - (d₁₃sinα₂p+d₃₃cosα₂q^P2) (d₁₃cosβ₂p-d₃₃sinβ₂q^S2)
c₄₄(sinα₁q^P1+cosα₁p) c₄₄(cosβ₁q^S1-sinβ₁p) d₄₄(sinα₂q^P2+cosα₂p) d₄₄(-cosβ₂q^S2+sinβ₂p)

Voici les coefficients obtenus pour une interface entre un milieu isotrope lent et un milieu isotrope transverse rapide dans le cas où une onde P est incidente dans le milieu isotrope :

anisopro.m

Winterstein D.F. and G. S. De, 2001, VTI documented montrent l'effet de l'isotropie transverse sur des ondes S enregistrées en sismique de puits 9 composantes.
Johnston, J. E. and Christensen, N. I. 1995, Seismic anisotropy of shales mesurent les vitesses de phase et de groupe sur des argiles.
Godfrey, N.J. ; Christensen, N. I. and Okaya, D.A. 2000, Anisotropy of schists: Contribution of crustal anisotropy to active source seismic experiments and shear wave splitting observations montrent l'importance de la contribution des schistes pour l'anisotropie dans la croûte.
Picotti, S., A. Vuan, J. M. Carcione, H. J. Horgan, and S. Anandakrishnan (2015), Anisotropy and crystalline fabric of Whillans Ice Stream (West Antarctica) inferred from multicomponent seismic data
Graebner M., 1992, Plane-wave reflection and transmission coefficients for a transversely isotropic solid

Atténuation

déplacement eq. équilibre	densité énergie cinétique (Jm^-3)	densité énergie élastique (Jm^-3)	densité puissance transportée P_t (Wm^-2)	intensité I (Wm^-2)
u(x,t) ρ∂²u/∂t² = ∂σ/∂x	w_c = (ρ/2)(∂u/∂t)² ∂w_c/∂t = (∂σ/∂x)(∂u/∂t)	w_e = ∫σdε = (E/2)ε² ∂w_e/∂t = σ∂/∂x(∂u/∂t)	∂(w_c+w_e)/∂t = ∂/∂x(σ∂u/∂t) P_t = -σ∂u/∂t	(1/T)∫₀^TP_tdt
u(x,t) = Ucos(kx-ωt)	w_c = (ρ/2)ω²U²sin²(kx-ωt)	w_e = (ρ/2)V²k²U²sin²(kx-ωt)	P_t = ρVω²U²sin²(kx-ωt) = V(w_c+w_e)	(ρ/2)Vω²U²
u = gradφ(x,t) ρ∂²u/∂t² = -gradp	w_c = (ρ/2)(∂u/∂t)² ∂w_c/∂t = -gradp.∂u/∂t	w_e = (K/2)(divu)² ∂w_e/∂t = -pdiv∂u/∂t	∫dx∂(w_c+w_e)/∂t = -∫dxdiv(p∂u/∂t) = -∫(p∂u/∂t).dS P_t = p∂u/∂t	(1/2)ℜ(p∂u*/∂t)

2π/facteur de qualité = énergie dissipée par cycle / énergie élastique maximum cycle = λ amplitude déplacement vitesse complexe V_Q = V(1-i/2Q)
2π/Q = -(δw)_cycle/w_max π/Q = -(dU/dx)λ/U U(x) = Ue^-αx
α = π/Qλ = k/2Q = ω/2QV u(x,t) = Ue^-αxcos(kx-ωt) u(x,t) = Ue^-αxe^iω(x/V-t) = Ue^{iω(x(1+i/2Q)/V-t)}
u(x,t) = Ue^iω(x/V_Q-t)

viscoélasticité linéaire énergie dissipée par cycle énergie élastique maximum facteur de qualité
σ = σ_mcos(ωt+χ)
ε = ε_mcosωt (δw)_cycle = ∫₀^Tσdε = πσ_mε_msinχ w_max = ∫₀^T/4σdε ≈ -(1/2)σ_mε_mcosχ 1/Q = tgχ ≈ χ

modèle viscoélastique , module élastique E , viscosité η nombre d'onde complexe k+iα faible atténuation , 1/Q << 1 1/Q < 1 , dispersion V(ω) = ω/k
E et η en parallèle, temps relaxation τ = η/E
σ = Eε+η∂ε/∂t = E(1-iωτ)ε = Mε
M = E(1+ω²τ²)^½e^-iχ , 1/Q = tgχ = ωτ ρ∂²u/∂t² = E(1-i/Q)∂²u/∂x²
ρω² = E(1-i/Q)(k+iα)² , k₀² = ρω²/E
k₀² = (1-i/Q)(k+iα)² k+iα = k₀(1+i/2Q)
k = k₀ , V = V₀ = ω/k₀
α = k₀/(2Q) = ω²τ/(2V₀) k²+α² = k₀²/(1+1/Q²)^½ ≈ k₀²(1-1/2Q²)
k²-α² = k₀²/(1+1/Q²) ≈ k₀²(1-1/Q²)
V(ω) ≈ V₀(1+3/(8Q²)) = V₀(1+3ω²τ²/8) , α = k₀/(2Q)
(E et η en parallèle) en série avec E' , σ = M''ε
1/M'' = 1/M+1/E' = 1/E(1-iωτ)+1/E' = (1/E+1/E'-iωτ/E')/(1-iωτ)
1/E'' = 1/E+1/E' , τ'' = τE''/E' , M'' = E''(1-iωτ)/(1-iωτ'') = ||M''||e^-i(χ-χ'')
1/Q = tg(χ-χ'') = ω(τ-τ'')/(1+ω²ττ'')
d(1/Q)/dω = 0 pour ω_r = (ττ'')^-½ et (1/Q)_max = (τ-τ'')/2(ττ'')^½
ρω² = M''(k+iα)² , k''₀² = ρω²/E''
k²+α² = ρω²/||M''|| = k''₀²(1+ω²τ''²)^½/(1+ω²τ²)^½
k²-α² = ρω²ℜ(1/M'') = k''₀²(1+ω²ττ'')/(1+ω²τ²)
k² = ω²/V(ω)² = (k''₀²/2)((1+ω²τ''²)^½/(1+ω²τ²)^½+(1+ω²ττ'')/(1+ω²τ²))

modèle à Q constant (Kjartansson, 1979, JGR, 84, 4737)
M = M₀(iω/ω₀)^2γ = M₀(|ω/ω₀|)^2γe^{iπγsign(ω)}
1/Q = tg(πγ) ρω² = M₀(|ω/ω₀|)^2γe^{iπγsign(ω)}(k+iα)²
k²+α² = k₀²(|ω/ω₀|)^-2γ
k²-α² = k₀²(|ω/ω₀|)^-2γcos(πγ) k = k₀(|ω/ω₀|)^-γcos(πγ/2)
V(ω) = V₀(|ω/ω₀|)^γ/cos(πγ/2)
α = k₀(|ω/ω₀|)^-γsin(πγ/2) = ktg(πγ/2) dispersion pour 1/Q << 1
V(ω)/V₀ ≈ (|ω/ω₀|)^1/πQ = e^{Log(|ω/ω₀|)/πQ}
V(ω)/V₀ ≈ 1+Log(|ω/ω₀|)/πQ

Sun, L.F., B. Milkereit, and D. R. Schmitt, 2009 Measuring velocity dispersion and attenuation in the exploration seismic frequency band mettent en évidence la dispersion et l'atténuation sur des données vibrosismiques.

Poroélasticité et vitesses dans les roches saturées en fluide

La porosité Φ est la proportion volumique d'espace poreux Ω_Φ dans un volume élémentaire Ω. Seuls les pores interconnectés dans lesquels un fluide peut s'écouler interviennent dans Φ, qui atteint 30% pour certains grès. Pour une porosité saturée par un fluide, le volume de fluide Ω_f est égal au volume des pores. On considère une déformation volumique ε de la roche due à une variation de la pression de confinement -σ. L'augmentation ζ du contenu volumique en fluide est due à l'augmentation du volume des pores et à la compression volumique du fluide.

Φ = Ω_Φ/Ω = Ω_f/Ω ε = δΩ/Ω ζ = (δΩ_Φ-δΩ_f)/Ω = Φ(δΩ_Φ/Ω_Φ-δΩ_f/Ω_f) = Φ(ε_Φ-ε_f)

La théorie de la poroélasticité linéaire isotrope exprime ε et ζ comme une combinaison linéaire de σ et p_f , la variation de pression de fluide dans les pores. La signification des coefficients de proportionnalité α (coefficient de Biot-Willis) et B (coefficient de Skempton) apparaît en considérant les cas d'une roche drainée (pression de fluide constante, incompressibilité K), non-drainée (contenu en fluide constant, incompressibilité K_sat) et d'une pression différentielle nulle (pressions de confinement et de fluide égales). Dans ce dernier cas, la déformation homogène est celle de la roche sans pore d'incompressibilité K₀ et la déformation volumique ε_Φ des pores est égale à la déformation volumique ε de la roche : on obtient ainsi la relation de Gassmann entre K_sat, K₀ , K , K_f (l'incompressibilité du fluide) et Φ. Cette relation permet de déterminer la vitesse de propagation des ondes de compression dans les roches poreuses saturées en fluide à basse fréquence (f < 100Hz).

poroélasticité linéaire ε = (1/K)(σ+αp_f)
ζ = (α/K)(σ+p_f/B) incompressibilité coef. poroélastiques
p_f = 0 ε = (1/K)σ K α = ζ/ε
ζ = 0 ε = ((1-αB)/K))σ K = (1-αB)K_sat B = -p_f/σ
σ = -p_f ε = ((1-α)/K))σ = σ/K₀ K = (1-α)K₀ .
ε_Φ = ζ/Φ+ε_f = ε
ε_f = -p_f/K_f (α/ΦK)(1-1/B)+1/K_f = 1/K₀ 1/B = 1-(ΦK/α)(1/K₀-1/K_f) = α/(1-K/K_sat)
relation de Gassmann 1/K_sat = (1-α)/K+α/K(1-1/(1-(ΦK/α)(1/K₀-1/K_f)))
1/K_sat = 1/K₀+Φ/(ΦK/α+1/(1/K_f-1/K₀))
1/(1/K_sat-1/K₀) = K/α+1/(Φ(1/K_f-1/K₀)) = 1/(1/K-1/K₀)+1/(Φ(1/K_f-1/K₀))
densité et vitesses ρ = (1-Φ)ρ₀+Φρ_f V_P² = (K_sat+4μ/3)/ρ V_S² = μ/ρ

Wang Z., 2001, Fundamentals of seismic rock physics montre comment la relation de Gassmann est utilisée dans l'étude sismique des réservoirs.
Smith, T.M., C. H. Sondergeld, and C. S. Rai, 2003, Gassmann fluid substitutions: A tutorial

Réflexion 1D sur gradient de vitesse (ρ=cte)

couches	déplacements	continuité u et σ en z=0 et z=H
z<0 V=V₀	u(z) = e^iωz/V₀+Re^-iωz/V₀	1+R = AV₀ⁿ+BV₀^m (iω/V₀)(1-R) = a(AnV₀^n-1+BmV₀^m-1) Te^iωH/V₁ = AV₁ⁿ+BV₁^m (iω/V₁)Te^iωH/V₁ = a(AnV₁^n-1+BmV₁^m-1) ⇒ B/A = -V₁^n-m(n-iω/a)/(m-iω/a)
0≤z≤H V(z)=V₀+az	-ρω²u(z) = ∂/∂z(ρV(z)²∂u/∂z) u(z) = A(V₀+az)ⁿ+B(V₀+az)^m n,m = -1/2±(1/4-ω²/a²)^½ n-m = 2(1/4-ω²/a²)^½
z>H V=V₁	u(z) = Te^iωz/V₁
	R = -(V₀^n-m-V₁^n-m)/((n+iω/a)/(n-iω/a)V₀^n-m-(m+iω/a)/(m-iω/a)V₁^n-m) = 1/(2iω/a+(n-m)(V₀^n-m+V₁^n-m)/(V₀^n-m-V₁^n-m))

Liner, C. and Bodmann, B. (2010). The Wolf ramp: Reflection characteristics of a transition layer
Chapman, N.R., J. F. Gettrust, R. Walia, D. Hannay, G. D. Spence, W. T. Wood, and R.D. Hyndman , 2002, High-resolution, deep-towed, multichannel seismic survey of deep-sea gas hydrates off western Canada
Wolf, A., 1937, The reflection of elastic waves from transition layers of variable velocity Read More: http://library.seg.org/doi/ref/10.1190/1.3476312

Réflexion-transmission d'une onde monochromatique sur une couche ou une stratification

La réflexion (transmission) d'une onde plane monochromatique SH sur (à travers) une couche d'épaisseur H incluse dans un espace homogène est formée par interférence entre la réflexion (transmission) primaire en entrant dans (à travers) la couche et les réflexions multiples qui sortent de la couche dans la direction de réflexion (transmission). Si R_e et T_e=(1+R_e) sont les coefficients de réflexion et transmission en entrant dans la couche, R_s=(-R_e) et T_s=(1-R_e) en sortant de la couche, et k_z le nombre d'onde vertical dans la couche, les coefficients R_H et T_H sont donnés par la somme des termes de la série des multiples successifs. Pour R_e<<1, il suffit de prendre en compte le premier terme de la série :

R_H1 = R_e+1 réflexion dans la couche , R_e<<1 , T_eT_s = 1-R_e² ≈ 1 R_Hn = R_e+n réflexions dans la couche , R_H = R_Hn (n→∞) R_H1 , R_H , T_H1, T_H
R_H1 = R_e+T_ee^ik_zHR_se^ik_zHT_s = R_e(1-(1-R_e²)e^2ik_zH) ≈ R_e(1-e^2ik_zH)
R_H1 = 0 pour k_zH=nπ ou λ_z = 2H/n
R_H1 = 2R_e pour k_zH=(2n+1)π/2 ou λ_z = 4H/(2n+1) R_Hn = R_e+T_eR_sT_se^2ik_zH(1+∑(R_se^ik_zH)²ⁿ)
R_H = R_e(1-(1-R_e²)e^2ik_zH/(1-R_e²e^2ik_zH)) = R_e(1-e^2ik_zH)/(1-R_e²e^2ik_zH)
légende reflcou
T_H1 = T_ee^ik_zHT_s = (1-R_e²)e^ik_zH ≈ e^ik_zH T_Hn = T_ee^ik_zHT_s(1+∑(R_se^ik_zH)²ⁿ)
T_H = (1-R_e²)e^ik_zH/(1-R_e²e^2ik_zH)

Alternativement, on peut considérer qu'il y a une onde montante (déplacement u_y pour une onde SH, potentiel φ pour une onde P acoustique) et une onde descendante dans la couche, somme respectivement de toutes les ondes montantes et descendantes dans cette couche. Pour une stratification, les ondes montantes et descendantes dans deux couches ayant une interface commune sont liées par des relations de continuité. On obtient les coefficients de réflexion-transmission sur la stratification en remontant depuis l'interface avec le demi-espace inférieur et en utilisant itérativement ces relations (le tableau se lit de bas en haut). Inversement, on obtient les coefficients de réflexion sur les interfaces à partir des rapports onde montante/descendante dans chaque couche. Le calcul des coefficients de réflexion-transmission sur la stratification pour différentes fréquences permet d'obtenir la trace sismique en temps par transformée de Fourier inverse (sommation des réponses harmoniques, sujette aux problèmes numériques d'échantillonnage et de périodicité). Pour tenir compte de la surface libre (R = 1), il suffit d'utiliser l'onde réfléchie par la stratification et par la surface libre comme onde descendante, et ainsi de suite pour obtenir les réflexions multiples successives dues à la surface libre.

couche
R_interface ondes descendantes
D_j = T_j+1D_j+1e^ik_zjh_j-R_j+1M_je^2ik_zjh_j
D_j+1 = (D_je^-ik_zjh_j+R_j+1M_je^ik_zjh_j)/T_j+1 ondes montantes
M_j+1 = R_j+1D_j+1+(1-R_j+1)M_je^ik_zjh_j
M_j+1 = (R_j+1D_je^-ik_zjh_j+M_je^ik_zjh_j)/T_j+1 coef. réflexion sur stratification
R_h1..j = M_j+1/D_j+1
R_j+1 = (R_h1..je^-ik_zjh_j-R_h1..j-1e^ik_zjh_j)/(e^-ik_zjh_j-R_h1..j-1R_h1..je^ik_zjh_j) coef. transmission par stratification
T_h1..j = D₀/D_j+1
couche 3
R₃ D₃ = (e^-ik_z2h₂+R₃R_h1e^ik_z2h₂)D₂/T₃ M₃ = (R₃e^-ik_z2h₂+R_h1e^ik_z2h₂)D₂/T₃ R_h12 = M₃/D₃
R₃ = (R_h12e^-ik_z2h₂-R_h1e^ik_z2h₂)/(e^-ik_z2h₂-R_h1R_h12e^ik_z2h₂) T_h12 = D₀/D₃ = T_h1D₂/D₃
couche 2
R₂ D₂ = (e^-ik_z1h₁+R₂R₁e^ik_z1h₁)D₁/T₂ M₂ = (R₂e^-ik_z1h₁+R₁e^ik_z1h₁)D₁/T₂ R_h1 = M₂/D₂
R₂ = (R_h1e^-ik_z1h₁-R₁e^ik_z1h₁)/(e^-ik_z1h₁-R₁R_h1e^ik_z1h₁) T_h1 = D₀/D₂ = T₁D₁/D₂
couche 1
R₁ D₁ M₁ R₁ = M₁/D₁ T₁ = D₀/D₁
1/2 espace D₀ M₀ = 0
stratif.m

Pour des ondes P-SV, il y a deux ondes (potentiels φ et &psi_y) montantes et deux ondes descendantes dans chaque couche. On obtient les coefficients de réflexion-transmission sur la stratification en calculant la matrice de transfert de la stratification, produit des matrices de transfert dans chaque couche. Sur l'interface inférieure de la stratification avec le demi-espace sous-jacent, les ondes montantes sont les ondes descendantes réfléchies. Dans le demi-espace sus-jacent les ondes descendantes sont les ondes incidentes choisies (P et/ou SV) et les rapports montantes/descendantes donnent les coefficients de réflexion. Si la stratification est sous l'eau (sismique marine), il faut multiplier la matrice de transfert précédente par la matrice calculée à l'interface liquide-solide.

ondes descendantes P et SV
D_Pj = (T_PPj+1D_Pj+1+T_SPj+1D_Sj+1+R^PPj+1M_Pje^ik_zPjh_j+R^SPj+1M_Sje^ik_zSjh_j)e^ik_zPjh_j
D_Sj = (T_PSj+1D_Pj+1+T_SSj+1D_Sj+1+R^PSj+1M_Pje^ik_zPjh_j+R^SSj+1M_Sje^ik_zSjh_j)e^ik_zSjh_j ondes montantes P et SV
M_Pj+1 = R_PPj+1D_Pj+1+R_SPj+1D_Sj+1+T^PPj+1M_Pje^ik_zPjh_j+T^SPj+1M_Sje^ik_zSjh_j
M_Sj+1 = R_PSj+1D_Pj+1+R_SSj+1D_Sj+1+T^PSj+1M_Pje^ik_zPjh_j+T^SSj+1M_Sje^ik_zSjh_j
(T_PPj+1T_SSj+1-T_PSj+1T_SPj+1)D_Pj+1
(T_SPj+1T_PSj+1-T_SSj+1T_PPj+1)D_Sj+1
T_SSj+1e^-ik_zPjh_j -T_SPj+1e^-ik_zSjh_j (T_SPj+1R^PSj+1-T_SSj+1R^PPj+1)e^ik_zPjh_j (T_SPj+1R^SSj+1-T_SSj+1R^SPj+1)e^ik_zSjh_j) D_Pj
D_Sj
M_Pj
M_Sj
T_PSj+1e^-ik_zPjh_j -T_PPj+1e^-ik_zSjh_j (T_PPj+1R^PSj+1-T_PSj+1R^PPj+1)e^ik_zPjh_j (T_PPj+1R^SSj+1-T_PSj+1R^SPj+1)e^ik_zSjh_j)
M_Pj+1
M_Sj+1
R_PPj+1 R_SPj+1 T^PPj+1e^ik_zPjh_j T^SPj+1e^ik_zSjh_j D_Pj+1
D_Sj+1
M_Pj
M_Sj
R_PSj+1 R_SSj+1 T^PSj+1e^ik_zPjh_j T^SSj+1e^ik_zSjh_j
1 (0)
0 (1)
R_PPh1.n (R_SPh1.n)
R_PSh1.n (R_SSh1.n) DM(4,4) = ∏ matrices transfert dans couches 1 à n 1
0
R_PP1
R_PS1 0
1
R_SP1
R_SS1 D_P1
D_S1
cas liquide-solide
D_Pj = (T_PPj+1D_Pj+1+R^PPj+1M_Pje^ik_zPjh_j+R^SPj+1M_Sje^ik_zSjh_j)e^ik_zPjh_j M_Pj+1 = R_PPj+1D_Pj+1+T^PPj+1M_Pje^ik_zPjh_j+T^SPj+1M_Sje^ik_zSjh_j
1
R_PPeau.h1.n DM_liq-sol(2,4) DM(4,4) 1
0
R_PP1
R_PS1 0
1
R_SP1
R_SS1 D_P1
D_S1

Voici les potentiels de déplacement calculés avec cette méthode en utilisant un modèle de vitesses-densité stratifié type Mer du Nord pour des paramètres d'ondes planes correspondant à des angles d'incidence dans l'eau θ = 0°, 15° et 30° dans les cas correspondant à la sismique réflexion terrestre (réflexion P-P et SV-SV sans eau) , à la sismique réflexion marine (réflexion P-P dans l'eau) et à la sismique réflexion marine avec enregistrement au fond de l'eau (réflexion P et SV sous l'eau pour une onde P incidente dans l'eau).
- - - -
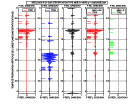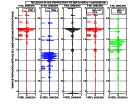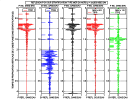
stratifpsv.m

Liu Y. and D. R. Schmitt, 2003, Amplitude and AVO responses of a single thin bed
Chapman, C. H., 2003, Yet another elastic plane-wave, layer-matrix algorithm donne un programme plus élaboré, utilisable pour des incidences supérieures à l'incidence critique.

Monitoring sismique en milieu élastique stratifié

La sismique réflexion est utilisable pour détecter les changements de propriétés élastiques (vitesses, densité, atténuation) dans le sous-sol. Il faut répéter des expériences identiques et détecter les changements dans les enregistrements (temps de trajet, amplitudes, forme d'ondes, fréquences ....) dus aux modifications du milieu sous-jacent. La méthode ci-dessus est utilisable pour simuler les changements correspondant à des modèles différents. Même si l'on ne modifie les propriétés élastiques que dans une couche fine, correspondant par exemple à un réservoir en production, toutes les arrivées ayant traversé cette couche sont affectées. L'exemple suivant montre ce qui se passe pour des ondes planes P et SV se propageant dans un modèle simple comportant une couche de 40 m d'épaisseur à 1000 m de profondeur dans laquelle la vitesse V_P diminue de 3200 à 2800 m/s, les autres paramètres étant inchangés.

- - - -
monitorpsv.m

Réflexion-transmission d'une onde SH sur une stratification cyclique

Si l'onde est incidente sur une stratification cyclique constituée d'une alternance régulière de 2 couches telles que les coefficients de réflexion-transmission à chaque interface soient alternativement (R_e,T_e) et (R_s,T_s) , l'effet des réflexions multiples de même ordre sur les différentes interfaces est cumulatif. Pour un grand nombre d'interfaces, les modules des termes du coefficient de transmission tenant compte des premiers multiples dans chaque couche sont supérieurs à celui de la transmission directe. En supposant que k_zH est le même dans les 2 couches et que la stratification comporte 2m+1 couches (2m+2 interfaces), les premiers termes du coefficient de transmission sont :

1 trajet à (T_eT_s)^m+1 T_S0 = T_ee^ik_zHT_s∏(e^ik_zHT_ee^ik_zHT_s) = (1-R_e²)^m+1e^(2m+1)ik_zH
transtrat.m
N₁(2m+1) = 2m+1 trajets à R² T_S1 = T_S0N₁(2m+1)R_e²e^2ik_zH
N₂(2m+1) = N₁(2m+1)+...+N₁(1) trajets à R⁴
N₁(2m) trajets à -R²,T_eT_s T_S2 = T_S0(N₂(2m+1)R_e⁴
-N₁(2m)(1-R_e²)R_e²)e^4ik_zH
N₃(2m+1) = N₂(2m+1)+...+N₂(1) trajets à R⁶
2N₂(2m+1)-2 trajets à -R⁴,T_eT_s
N₁(2m-1) trajets à R²,(T_eT_s)² T_S3 = T_S0(N₃(2m+1)R_e⁶
-(2N₂(2m+1)-2)(1-R_e²)R_e⁴
+N₁(2m-1)(1-R_e²)²R_e²)e^6ik_zH
N₄(2m+1) = N₃(2m+1)+...+N₃(1) trajets à R⁸
3N₃(2m+1)+N₂(2m)-3 trajets à -R⁶,T_eT_s
3N₂(2m+1)-N₂(2)-2 trajets à R⁴,(T_eT_s)²
N₁(2m-2) trajets à -R²,(T_eT_s)³ T_S4 = T_S0(N₄(2m+1)R_e⁸
-(3N₃(2m+1)+N₂(2m)-3)(1-R_e²)R_e⁶
+(3N₂(2m+1)-N₂(2)-2)(1-R_e²)²R_e⁴
+N₁(2m-2)(1-R_e²)³R_e²)e^8ik_zH

Les termes successifs des coefficients de transmission et réflexion sont calculables sans avoir à dénombrer tous les trajets possibles en utilisant les récurrences reliant les ondes montantes M_j,n+1 et descendantes D_j,n+1 de part et d'autre de chaque interface j après n+1 réflexion-transmissions à celles provenant des interfaces immédiatement au dessus D_j-1,n et en dessous M_j+1,n après n réflexion-transmissions. On obtient ainsi les réponses impulsionelle et harmonique complètes de la stratification. Les réponses impulsionnelles en réflexion et transmission sont caractérisées par des codas avec une amplitude décroissant exponentiellement. Les réponses harmoniques sont caractérisées par des pics de réflectivité (trous de transmissivité) pour H=(2n+1)λ_z/4 .

initialisation réflexion-transmission sur interface impaire réflexion-transmission sur interface paire
refltranstrat.m
M_1,1 = R_e , D_1,1 = T_e
M_2,2 = R_sT_ee^ik_zH , D_2,2 = T_sT_ee^ik_zH R_2n+1 = M_1,2n+1 = T_sM_2,2ne^ik_zH
D_1,2n+1 = R_sM_2,2ne^ik_zH
M_2j+1,2n+1 = (R_eD_2j,2n+T_sM_2j+2,2n)e^ik_zH
D_2j+1,2n+1 = (T_eD_2j,2n+R_sM_2j+2,2n)e^ik_zH M_2j,2n+2 = (R_sD_2j-1,2n+1+T_eM_2j+1,2n+1)e^ik_zH
D_2j,2n+2 = (T_sD_2j-1,2n+1+R_eM_2j+1,2n+1)e^ik_zH
M_2m+2,2n+2 = R_sD_2m+1,2n+1e^ik_zH
T_2n+2 = D_2m+2,2n+2 = T_sD_2m+1,2n+1e^ik_zH

Anstey N.A. and R. F. O'Doherty, 2002, Cycles, layers, and reflections: Part 1 expliquent l'origine des réflexions observées dans les bassins sédimentaires caractérisés par une sédimentation cyclique.
Stewart, R.R., P. D. Huddleston, and T. K. Kan, 1984, Seismic versus sonic velocities: A vertical seismic profiling study expliquent la différence entre les vitesses mesurées localement et depuis la surface dans un puits par l'effet de stratification cyclique.

Relations réflexion-transmission par une stratification

On obtient des relations entre les coefficients de réflexion-transmission pour des ondes incidentes par en haut ou par en bas sur la stratification en remarquant qu'une inversion du signe du temps inverse le sens de propagation de toutes les ondes harmoniques et remplace leurs amplitudes complexes par leurs conjuguées (les retards de phase correspondant au temps de propagation vertical dans la stratification deviennent des avances). La propagation dans la stratification des ondes réfléchies et transmises auxquelles ce retournement temporel a été préalablement appliqué reconstitue l'onde incidente initiale. En effet, les ondes refont le même chemin en sens inverse et arrivent en phase sur les plans limitant la stratification.

cas SH onde incidente en haut (a) onde incidente en bas (b) retournement (a) + propagation retournement (b) + propagation
sens propagation ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑
haut 1 R_h 0 t_h R_h* 1 = R_hR_h*+t_hT_h* t_h* 0 = R_ht_h*+t_hr_h*
bas T_h 0 r_h 1 0 = T_hR_h*+r_hT_h* T_h* 1 = T_ht_h*+r_hr_h* r_h*

Pour le cas d'une couche d'épaisseur H dans un milieu homogène, R_e étant le coefficient de réflexion SH sur l'interface à l'entrée de la couche, on vérifie :

couche onde incidente en haut (a) onde incidente en bas (b) retournement (a) + propagation
haut 1 R_h = R_e(1-e^2ik_zH)/(1-R_e²e^2ik_zH) 0 t_h = T_h R_hR_h*+t_hT_h* = (R_e²(1-e^2ik_zH)(1-e^-2ik_zH)+ (1-R_e²)²) /((1-R_e²e^2ik_zH)(1-R_e²e^-2ik_zH)) = 1
bas T_h = (1-R_e²)e^ik_zH/(1-R_e²e^2ik_zH) 0 r_h = R_h 1 T_hR_h*+r_hT_h* = R_e(1-R_e²)(e^ik_zH(1-e^-2ik_zH)+e^-ik_zH(1-e^2ik_zH)) /((1-R_e²e^2ik_zH)(1-R_e²e^-2ik_zH)) = 0

Par ailleurs, les flux d'énergie entrant et sortant de la stratification doivent être égaux.

impédance SH x cos(incidence) onde incidente en haut onde incidente en bas
flux énergie entrant sortant entrant sortant
haut : I_a = (ρV_Scosη)_haut I_a I_aR_hR_h* 0 I_at_ht_h*
bas : I_b = (ρV_Scosη)_bas 0 I_bT_hT_h* I_b I_br_hr_h*
conservation flux I_a(1-R_hR_h*) = I_bT_hT_h* I_b(1-r_hr_h*) = I_at_ht_h*
relations transmission/réflexion t_hT_h* = 1-R_hR_h* = 1-r_hr_h* = (I_b/I_a)T_hT_h* t_h = (I_b/I_a)T_h R_hR_h* = r_hr_h*

Si la stratification est limitée par une surface libre, il y a réflexion totale sur celle-ci. Pour une onde incidente descendante, la réponse en réflexion de la stratification est renvoyée vers le bas. L'autocorrélation de la réponse en transmission descendante D dans le demi-espace sous la stratification est proportionnelle à la somme de l'onde incidente, de la réponse en réflexion et de sa retournée temporelle. De même, pour une onde incidente montante, l'autocorrélation de la réponse en transmission montante M dans la couche sous la surface libre est proportionnelle à la somme de l'onde incidente, de la réponse en réflexion et de sa retournée temporelle.

onde incidente transmission + 1 réflexion sur surface libre autocorrélation réflexion + retournée temporelle
descendante dans couche D = T_h(1+R_h) DD* = T_hT_h*(1+R_h)(1+R_h)* = (I_a/I_b)T_ht_h*(1+R_h)(1+R_h)* = (I_a/I_b)(1-R_hR_h*)(1+R_h)(1+R_h)* DD* ≈ (I_a/I_b)(1+R_h+R_h*)
montante dans demi-espace M = t_h(1+R_h) MM* = t_ht_h*(1+R_h)(1+R_h)* = (I_b/I_a)T_ht_h*(1+R_h)(1+R_h)* = (I_b/I_a)(1-R_hR_h*)(1+R_h)(1+R_h)* MM* ≈ (I_b/I_a)(1+R_h+R_h*)

Réflexion-diffusion d'une onde acoustique plane sur une surface libre faiblement ondulée

Une surface libre présentant une ondulation sinusoïdale z=h(x) de la topographie autour du plan z=0 perturbe la réflexion d'une onde plane. Pour une ondulation de faible amplitude, on considère que la surface engendre une onde réfléchie sur un plan horizontal z=0 selon la loi de Snell plus une onde diffusée par les ondulations. On obtient une approximation de l'onde harmonique diffusée p_s(x,z) à partir de l'onde harmonique p₀(x,z) se propageant en l'absence de perturbation en supposant que P_s<<P₀ et en faisant un développement limité de la condition au limite (pression nulle) qui s'applique sur l'interface ondulée.

onde harmonique incidente+réfléchie sur surface libre z=0 pression nulle sur surface libre
z = h(x) = He^ik_hx onde = p₀ + onde diffusée P_s<<P₀
k_z0H<<1 onde harmonique diffusée dans la direction θ_s
p₀(x,z) = P₀e^ik_x0x(e^-ik_z0z-e^ik_z0z)
p₀(x,0) = 0
p(x,h(x)) = 0
p(x,0)+h(x)∂p/∂z(x,0) ≈ 0
p(x,z) = (p₀+p_s)(x,z)
p_s(x,0) = -h(x)∂(p₀+p_s)/∂z(x,0)
p_s(x,0) ≈ -h(x)∂p₀/∂z(x,0)
p_s(x,0) =P_se^ik_xsx
P_s = -2ik_z0HP₀
k_xs = (k_x0+k_h)
p_s(x,z) = P_se^ik_xsxe^ik_zsz
sinθ_s = sinθ₀+Vk_h/ω
k_zs = (ω²/V²-k_xs²)^½

Bibliographie

ROYER D. et DIEULESAINT E., 1996, Ondes élastiques dans les solides. Tome 1 : propagation libre et guidée, Masson, Springer

ACHENBACH J.D., 1973, Wave propagation in elastic solids, North-Holland
BREKHOVSKIKH L.M. ; LYSANOV Y.P., 1991, Fundamentals of Ocean Acoustics, Springer
CLAERBOUT J.F., 1976, Fundamentals of Geophysical Data Processing, McGraw-Hill
LAY T. , WALLACE T. C., 1995, Modern global seismology, Academic Press
MAVKO G. , MUKERJI T. , DVORKIN J., 1998, The rock physics handbook. Tools for seismic analysis in porous media, Cambridge
MULLER G., Theory of elastic waves, Samizdat Press
OFFICER C.B., 1958, Introduction to the theory of sound transmission, McGraw Hill
UDIAS A., 1999, Principles of seismology, Cambridge
WHITE J.E., 1965, Seismic waves : radiation, transmission and attenuation, McGraw-Hill

FOUQUE F., 1888, Les tremblements de terre, Baillière et fils, Paris , décrit les premières tentatives de mesures des vitesses de propagation des ondes sismiques dans les formations géologiques dans un livre consacré aux débuts de la science sismologique instrumentale et expérimentale. Comme les mesures avec des sources et des récepteurs en surface s'avéraient peu concluantes avec l'instrumentation disponible, les mesures les plus significatives ont été obtenues avec des sources placées dans des galeries de mine et des récepteurs en surface. Ces configurations sont toujours utilisées en sismique de puits. Par ailleurs, le livre montre des enregistrements démontrant la propagation à grande distance des ondes sismiques issues des tremblements de terre, un sujet de controverse à l'époque.

grandeur	unité	notation	composantes	ordres de grandeur
longueur d'onde	m	λ	.	10^-3 m (grains dans les roches) - 10⁷ m (taille de la Terre)
période fréquence pulsation	s Hz rad/s	T f = 1/T ω = 2πf	.	10⁶ Hz (ultrasons sur échantillons) - 10^-3 Hz (vibrations propres de la Terre)
vitesses de propagation ondes P, S	m/s	V_P V_S	légende mernord	10² m/s (V_S dans les sols) - 10⁴ m/s (V_P dans le manteau) V_P/V_S : 1.7 dans les roches consolidées, >10 dans les sols peu consolidés saturés en eau
densité impédances	kg/m³ kg/m²/s	ρ I = ρV	légende mernord	10³ kg/m³ (eau) - 10⁴ kg/m³ (noyau)
déplacement des particules	m	u	u_x , u_y , u_z	U : 1 m (glissement sur faille) - 10^-8m (bruit ambiant)
vitesse des particules	m/s	∂u/∂t	∂u_x/∂t , ∂u_y/∂t , ∂u_z/∂t	U/T - voir les définitions des différentes échelles de magnitudes à partir du rapport U/T
accélération des particules	m/s²	∂²u/∂t²	∂²u_x/∂t² , ∂²u_y/∂t² , ∂²u_z/∂t²	U/T² : 10 m/s²≈1g (épicentres des grands tremblements de terre) - 10^-11m/s² (vibrations propres de la Terre)
déformations	.	ε	ε_xx , ε_yy , ε_zz ε_xy , ε_yz , ε_zx	U/λ : 10^-6
contraintes	Pa	σ	σ_xx , σ_yy , σ_zz σ_xy , σ_yz , σ_zx	ρV²U/λ = IU/T : 10⁴ - 1 Pa (pressions enregistrées dans l'eau en sismique réflexion, f = 10-100Hz)
direction de propagation	.	e	e_x , e_y , e_z sinθ , 0 , cosθ	les sources sismiques émettent tous azimuts
vecteur d'onde	m^-1	k = (2π/λ)e	k_x , k_y , k_z	caractérise une onde plane harmonique
facteur de qualité	.	Q	.	∞ - 10 (sédiments peu consolidés)

.	module élastique	dilatation	cisaillement	variation volume
déformation	.	ε_xx = ∂u_x/∂x	ε_xy = (∂u_x/∂y+∂u_y/∂x)/2	divu = ε_xx+ε_yy+ε_zz
compression uniaxiale	module Young E coef. Poisson ν	σ_xx = Eε_xx ε_yy = -νε_xx	.	divu = (1-2ν)ε_xx
contrainte-déformation quelconque	coef. Lamé λ , μ incompressibilité K	σ_xx = λdivu+2με_xx	σ_xy = 2με_xy	divu = (σ_xx+σ_yy+σ_zz)/3K
relations entre modules	E = 10¹⁰ - 10¹¹ Pa ν = 0.2 - 0.4 (roches) ; 0.5 (eau)	λ = Eν/((1+ν)(1-2ν))	μ = E/(2(1+ν))	K = λ+2μ/3 = E/(3(1-2ν))

	air	eau	glace	calcite CaCO3	quartz SiO2	olivine (Mg,Fe)SiO4
K (GPa)	0.0001	2.4	8.4	70	37	130
μ (GPa)	0	0	3.6	29	44	80
ρ (kg/m³)	1	1000	920	2700	2700	3320

déformations	ε_rr = ∂u_r/∂r	ε_θθ = (1/r)(u_r+∂u_θ/∂θ)	ε_zz = ∂u_z/∂z	ε_zr = (∂u_r/∂z+∂u_z/∂r)/2	ε_rθ = ((1/r)(∂u_r/∂θ-u_θ)+∂u_θ/∂r)/2	ε_θz = ((1/r)∂u_z/∂θ+∂u_θ/∂z)/2
contraintes	σ_rr = λdivu+2με_rr	σ_θθ = λdivu+2με_θθ	σ_zz = λdivu+2με_zz	σ_zr = 2με_zr	σ_rθ = 2με_rθ	σ_θz = 2με_θz

Ondes de compression	onde longitudinale 1D	ondes acoustiques	ondes P
déplacement	u_x(x,t)	u = gradφ(x,t)	u = gradφ(x,t)
déformations	ε_xx = ∂u_x/∂x	divu = Δφ	ε_xx = ∂²φ/∂x² , ε_yy , ε_zz ε_xy = ∂²φ/∂x∂y , ε_yz , ε_zx
contraintes	σ_xx = E∂u_x/∂x	p = -Kdivu	σ_xx = λΔφ+2μ∂²φ/∂x² , σ_yy , σ_zz σ_xy = 2μ∂²φ/∂x∂y , σ_yz , σ_zx
équations d'équilibre	ρ∂²u_x/∂t² = ∂σ_xx/∂x	ρ∂²u/∂t² = -gradp	ρ∂²u_x/∂t² = ∂σ_xx/∂x+∂σ_xy/∂y+∂σ_xz/∂z ρ∂/∂x(∂²φ/∂t²) = (λ+2μ)∂/∂x(Δφ) ρgrad(∂²φ/∂t²) = (λ+2μ)grad(Δφ)
équation des ondes	∂²u_x/∂t² = V_L²∂²u_x/∂x²	∂²p/∂t² = V_A²Δp	∂²φ/∂t² = V_P²Δφ
vitesse de propagation	V_L² = E/ρ	V_A² = K/ρ	V_P² = (λ+2μ)/ρ

Ondes de cisaillement (divu = 0)	onde transverse 1D	ondes SH (polarisation ⊥ plan de propagation)	ondes SV(polarisation dans plan de propagation ⊥ direction de propagation)
déplacement	u_y(x,t)	u_y(x,z,t)	ψ = (0, ψ_y(x,z,t) ,0) , u(x,z,t) = rotψ(x,z,t) u_x = -∂ψ_y/∂z , u_z = ∂ψ_y/∂x
déformations	ε_xy = (1/2)∂u_y/∂x	ε_xy = (1/2)∂u_y/∂x , ε_yz	ε_xx = -∂²ψ_y/∂z∂x = -ε_zz ε_xz = (-∂²ψ_y/∂z²+∂²ψ_y/∂x²)/2
contraintes	σ_xy = μ∂u_y/∂x	σ_xy = μ∂u_y/∂x , σ_yz	σ_xx = -2μ∂²ψ_y/∂z∂x = -σ_zz σ_xz = μ(-∂²ψ_y/∂z²+∂²ψ_y/∂x²)
équations d'équilibre	ρ∂²u_y/∂t² = ∂σ_xy/∂x	ρ∂²u_y/∂t² = ∂σ_xy/∂x+∂σ_yz/∂z	ρ∂²u_x/∂t² = ∂σ_xx/∂x+∂σ_xz/∂z ρ∂/∂z(∂²ψ_y/∂t²) = μ∂/∂z(∂²ψ_y/∂x²+∂²ψ_y/∂z²)
équation des ondes	∂²u_y/∂t² = V_S²∂²u_y/∂x²	∂²u_y/∂t² = V_S²Δu_y	∂²ψ_y/∂t² = V_S²Δψ_y
vitesse de propagation	V_S² = μ/ρ	V_S² = μ/ρ	V_S² = μ/ρ

	grés mal consolidé	grés consolidé	calcaire	granite	basalte	granulite	dunite
V_P (km/s)	2.7	4.1	4.6	6.2	5.9	7.0	8.3
V_S (km/s)	1.4	2.4	2.4	3.7	3.2	3.8	4.8
ν = (V_P²/V_S²-2)/(2V_P²/V_S²-2)	0.32	0.24	0.31	0.22	0.29	0.29	0.25
ρ (kg/m³)	2100	2400	2400	2650	2880	3000	3300

onde 1D	ondes P	ondes S
u→ = u(x/V-t) u← = u(-x/V-t)	φ(e.x/V_P-t) u_longitudinal = gradφ = (e/V_P)φ'	ψ(e.x/V_S-t) u_transverse = rotψ = (e/V_S)∧ψ'
cas harmonique : u = Ue^iω(x/V-t) = Ue^{i2π(x/λ-t/T)} = Ue^i(kx-ωt) u→ : k = ω/V u← : k = -ω/V	φ = Φe^i(k.x-ωt) , k = (ω/V_P)e u = ikΦe^i(k.x-ωt)	ψ = Ψe^i(k.x-ωt) , k = (ω/V_S)e u = ik∧Ψe^i(k.x-ωt)

Δφ(r) = (1/r)∂²(rφ)/∂r² car Δφ(r) = divgradφ(r) = div(∂φ/∂re_r) = grad∂φ/∂r.e_r+∂φ/∂rdive_r = ∂²φ/∂r²+2/r∂φ/∂r (dive_r = 2/r car dive_r = div(r/r) = grad(1/r).r+divr/r et divr = ∂x/∂x+∂y/∂y+∂z/∂z = 3)
∂²(rφ)/∂t² = V_P²∂²(rφ)/∂r²	déplacement des particules	champ lointain : kr>>1	champ proche : kr<<1
φ = (A/r)f(±r/V_P-t)	u = (A/r)e_r(-f/r±f'/V_P)	u_cl = (±f'A/rV_P)e_r	u_cp = (-Af/r²)e_r
φ = (A/r)e^i(kr-ωt)	u = (A/r)e_r(ik-1/r)e^i(kr-ωt)	u_cl = (ikA/r)e_re^i(kr-ωt)	u_cp = (-A/r²)e_re^i(kr-ωt) A = -U₀r₀² pour source de rayon r₀<<λ

.	équation front onde	vitesses apparentes le long des axes	équation iconale : Pythagore pour les ondes
plan	T(x) = e.x/V	gradT = e/V	e.e=1 gradT.gradT = (∂T/∂x)²+(∂T/∂y)²+(∂T/∂z)² = 1/V² (1/V_ax)²+(1/V_ay)²+(1/V_az)² = 1/V²
sphérique	T(x) = r/V	gradT = e_r/V
quelconque	T(x)	gradT = e_M/V

Hodochrone T(X) des ondes directe, réfléchie, conique pour distance source-récepteurs SR=X et milieux homogènes de vitesses V₁ et V₂
pendage α	onde directe	onde réfléchie réflexion totale pour incidence θ₁>θ_c	onde conique (n'existe que si V₂>V₁) incidence critique θ_c : sinθ_c = V₁/V₂ ;
légende hodo direco.m	T = X/V₁	T = (4d²+X²)^½/V₁	distance et temps critique : X_c = 2dtgθ_c , T_c = 2d/cosθ_c/V₁ vitesses apparentes horizontale et verticale : V_ax = V₁/sinθ_c = V₂ ; V_az = V₁/cosθ_c temps de trajet : T = X/V_ax+2d/V_az = X/V₂+2dcosθ_c/V₁
légende hodop	T = X/V₁	source virtuelle symétrique de la source par rapport à l'interface x_v = 2dsinα ; z_v = 2dcosα T = (4(dcosα)²+(X±2dsinα)²)^½/V₁ + pour récepteurs vers l'aval - pour récepteurs vers l'amont	distance critique (triangle source virtuelle, projeté vertical de la SV sur surface, récepteur) : X_c = 2d(cosαtg(θ_c±α)-±sinα) = 2dsinθ/cos(θ±α) vitesses apparentes suivant et perpendiculairement à l'interface : V_aα = V₁/sinθ_c = V₂ ; V_a⊥α = V₁/cosθ_c distances suivant et perpendiculairement à l'interface : x_α = Xcosα ; d_⊥α = 2d±Xsinα temps de trajet : T = x_α/V_aα+d_⊥α/V_a⊥α T = Xcosα/V₂+(2d±Xsinα)cosθ_c/V₁ = Xsin(θ_c±α)/V₁+2dcosθ_c/V₁

loi de Snell : p = sinθ/V = (1/V_ax) = cte pour un rayon	paramètre du rayon	distance horizontale X(p) entre deux points d'un même rayon	temps de trajet T(p) entre deux points d'un même rayon
stratification plane horizontale (couches d'épaisseur d_i et vitesses constantes V_i) - légende hodostratif - hodostratif.m - hodostrat.m	réflexion p = sinθ_i/V_i	X(p) = ∑d_itgθ_i = p∑d_iV_i/(1-p²V_i²)^½	T(p) = ∑d_i/cosθ_iV_i = ∑d_i/(1-p²V_i²)^½V_i τ(p) = T(p)-pX(p) = ∑d_icosθ_i/V_i = ∑d_i(1-p²V_i²)^½/V_i
	conique p = sinθ_i/V_i = 1/V_n	X_cn = 2∑d_itgθ_i = 2∑d_i/(V_n²/V_i²-1)^½ si V_n > V_i, i = 1 à n-1 T = X/V_n+2∑d_icosθ_i/V_i = X/V_n+2∑d_i(1/V_i²-1/V_n²)^½ pour X > X_cn

e = -cosθ₁n+sinθ₁m	e_r = cosθ₁n+sinθ₁m	e_r-e = 2cosθ₁n = -2(e.n)n	e_r = e-2(e.n)n
e/V₁ = -cosθ₁/V₁n+sinθ₁/V₁m	e_t/V₂ = -cosθ₂/V₂n+sinθ₂/V₂m	e_t/V₂-e/V₁ = (cosθ₁/V₁-cosθ₂/V₂)n	e_t = V₂/V₁(e-(e.n+((V₁/V₂)²-(1-e.n²))^½)n)

s abscisse curviligne d'un rayon x(s) e = dx/ds	équation différentielle des rayons e.e = 1 , e.∂e/∂x = 0 , gradT.∂e/∂x = 0 ∂(dT/ds)/∂x = ∂(e.gradT)/∂x = e.grad∂T/∂x = d(∂T/∂x)/ds	courbure des rayons de/ds = e_N/R	torsion des rayons b = e∧e_N de_N/ds = -e/R-b/τ
gradT = e/V T = ∫ds/V(x(s))	d(e/V)/ds = d(gradT)/ds = grad(dT/ds) = grad(1/V)	1/R = Ve_N.grad(1/V)	1/τ = -Rb.d(Vgrad(1/V))/ds
cas V(x,z) = V₀+a_xx+a_zz = V₀+a(xsinα+zcosα) par une rotation d'angle α, on se ramène au cas V(Z) = V₀+aZ les rayons sismiques sont des cercles centrés sur la droite V(x,z) = 0	d(sinθ/V)/ds = -a_x/V² = -asinα/V² d(cosθ/V)/ds = -a_z/V² = -acosα/V²	1/R = dθ/ds = -a_xcosθ/V+a_zsinθ/V = asin(θ-α)/V

onde quasi plane (solution haute fréquence de l'éq. des ondes	terme en ω² → éq.iconale	terme en ω → éq. transport	tube de rayon de section dS(s)
φ = A(x)e^iω(T(x)-t)	gradT.gradT=1/V²	2gradA.gradT+AΔT = div(A²gradT) = 0	∫∫∫div(A²gradT)dυ = ∫∫(A²/V)e.dσ = 0 A²dS/V = cte

ω et k_x = ωp = ωsin(θ)/V_P = ωsin(η)/V_S de l'onde incidente sont les mêmes pour toutes les ondes réfléchies et transmises sur une interface plane horizontale
ondes descendantes : k_z^P = +ωcos(θ)/V_P , k_z^S = +ωcos(η)/V_S ondes montantes : k_z^P = -ωcos(θ)/V_P , k_z^S = -ωcos(η)/V_S	ondes SH	ondes P-SV
surface libre	σ_zy^{Incidente SH}+σ_zy^{Réfléchie SH} = 0	σ_zz^{Incidente P ou SV}+σ_zz^{Réfléchie P}+σ_zz^{Réfléchie SV} = 0 σ_zx^{Incidente P ou SV}+σ_zx^{Réfléchie P}+σ_zx^{Réfléchie SV} = 0
interface solide - solide	u_y^{Incidente SH}+u_y^{Réfléchie SH} = u_y^{Transmise SH} σ_zy^{Incidente SH}+σ_zy^{Réfléchie SH} = σ_zy^{Transmise SH}	u_x^{Incidente P ou SV}+u_x^{Réfléchie P}+u_x^{Réfléchie SV} = u_x^{Transmise P}+u_x^{Transmise SV} u_z^{Incidente P ou SV}+u_z^{Réfléchie P}+u_z^{Réfléchie SV} = u_z^{Transmise P}+u_z^{Transmise SV} σ_zz^{Incidente P ou SV}+σ_zz^{Réfléchie P}+σ_zz^{Réfléchie SV} = σ_zz^{Transmise P}+σ_zz^{Transmise SV} σ_zx^{Incidente P ou SV}+σ_zx^{Réfléchie P}+σ_zx^{Réfléchie SV} = σ_zx^{Transmise P}+σ_zx^{Transmise SV}
interface liquide - solide	.	u_z^{Incidente P}+u_z^{Réfléchie P} = u_z^{Transmise P}+u_z^{Transmise SV} σ_zz^{Incidente P}+σ_zz^{Réfléchie P} = σ_zz^{Transmise P}+σ_zz^{Transmise SV} σ_zx^{Transmise P}+σ_zx^{Transmise SV} = 0

loi de Snell : k_x = ωp = ωsinη₁/V_S1 = ωsinη₂/V_S2	onde incidente SH descendante	onde réfléchie SH montante	onde transmise SH descendante
déplacement onde SH u_y(x,z,t) = U_ye^ik_zze^i(k_xx-ωt)	U_y^I = 1 k_z^I = ωcosη₁/V_S1	U_y^R = R k_z^R = -ωcosη₁/V_S1	U_y^T = T k_z^T = ωcosη₂/V_S2
contrainte sur surface horizontale σ_zy(x,z,t) = μ∂u_y/∂z = ρV_S²ik_zu_y = iωS_zye^ik_zze^i(k_xx-ωt)	S_zy^I = ρ₁V_S1cosη₁	S_zy^R = -ρ₁V_S1cosη₁R	S_zy^T = ρ₂V_S2cosη₂T
continuité sur interface z =0 (u_y^I+u_y^R)(z=0) = u_y^T(z=0) (σ_zy^I+σ_zy^R)(z=0) = σ_zy^T(z=0)	1+R=T (1-R)ρ₁V_S1cosη₁ = Tρ₂V_S2cosη₂	R = (ρ₁V_S1cosη₁-ρ₂V_S2cosη₂)/(ρ₁V_S1cosη₁+ρ₂V_S2cosη₂)	T = 2ρ₁V_S1cosη₁/(ρ₁V_S1cosη₁+ρ₂V_S2cosη₂)
faible contraste ρ+δρ , V+δV δη = tgηδV/V (δp=0)		R ≈ -δ(ρVcosη)/2ρVcosη = -(1/2)(δρ/ρ+(1-tg²η)δV/V)	T ≈ 1
réflexion totale sinη_c=V_S1/V_S2 η₁>η_c , pV_S2>1	k_z^R = -k_z^I = -ω(1-p²V_S1²)^½/V_S1 R = (ρ₁V_S1(1-p²V_S1²)^½-iρ₂V_S2(p²V_S2²-1)^½)/(ρ₁V_S1(1-p²V_S1²)^½+iρ₂V_S2(p²V_S2²-1)^½) R = e^iχ(p) , χ(p) = -2Arctg(ρ₂V_S2(p²V_S2²-1)^½/ρ₁V_S1(1-p²V_S1²)^½) (u_y^I+u_y^R)(x,z,t) = (e^{ik_z^Iz}+e^{i(k_z^Rz+χ(p))})e^i(k_xx-ωt) = 2cos(k_z^Iz-χ(p)/2)e^{i(k_xx-ωt+χ(p)/2)}		onde transmise évanescente : k_z^T = iω(p²V_S2²-1)^½/V_S2 T = 2ρ₁V_S1(1-p²V_S1²)^½/(ρ₁V_S1(1-p²V_S1²)^½+iρ₂V_S2(p²V_S2²-1)^½) T = \|\|T\|\|e^iχ(p)/2 u_y^T(x,z,t) = \|\|T\|\|e^{-ωz(p²V_S2²-1)^½/V_S2}e^{i(k_xx-ωt+χ(p)/2)}

loi de Snell : k_x = ωp = ωsinθ₁/V_P1 = ωsinθ₂/V_P2	onde incidente P descendante	onde réfléchie P montante	onde transmise P descendante
déplacement u_z onde P u_z(x,z,t) = ∂φ/∂z = Φik_zφ	Φ^I = 1 k_z^I = ωcosθ₁/V_P1	Φ^R = R k_z^R = -ωcosθ₁/V_P1	Φ^T = T k_z^T = ωcosθ₂/V_P2
pression σ sur interface σ(x,z,t) = -KΔφ = ρV_P²k²φ = ω²Sφ	S^I = ρ₁	S^R = ρ₁R	S^T = ρ₂T
continuité sur interface z =0 (u_z^I+u_z^R)(z=0) = u_z^T(z=0) (σ^I+σ^R)(z=0) = σ^T(z=0)	(1-R)cosθ₁/V_P1 = Tcosθ₂/V_P2 (1+R)ρ₁ = Tρ₂	R = (ρ₂V_P2cosθ₁-ρ₁V_P1cosθ₂)/(ρ₁V_P1cosθ₂+ρ₂V_P2cosθ₁) u_z^R/u_z^I = -R	T = 2ρ₁V_P2cosθ₁/(ρ₁V_P1cosθ₂+ρ₂V_P2cosθ₁)
réflexion totale sinθ_c=V_P1/V_P2 θ₁>θ_c , pV_P2>1	k_z^R = -k_z^I = -ω(1-p²V_P1²)^½/V_P1 R = (ρ₂V_P2(1-p²V_P1²)^½-iρ₁V_P1(p²V_P2²-1)^½)/(ρ₂V_P2(1-p²V_P1²)^½+iρ₁V_P1(p²V_P2²-1)^½) R = e^iχ(p) , χ(p) = -2Arctg(ρ₁V_P1(p²V_P2²-1)^½/ρ₂V_P2(1-p²V_P1²)^½)		onde transmise évanescente : k_z^T = iω(p²V_P2²-1)^½/V_P2

loi de Snell : k_x = ωp = ωsinθ/V_P = ωsinη/V_S	onde incidente P montante	onde réfléchie P descendante	onde réfléchie SV descendante
potentiels de déplacement P et SV φ(x,z,t) = Φ e^{ik_z^Pz}e^i(k_xx-ωt) ψ_y(x,z,t) = Ψ e^{ik_z^Sz}e^i(k_xx-ωt)	Φ^I = 1 k_z^P = -ωcosθ/V_P	Φ^R = R_φ k_z^P = ωcosθ/V_P	Ψ^R = R_ψ k_z^S = ωcosη/V_S
contraintes exercées par onde P sur une surface horizontale σ_zz^P = λΔφ+2μ∂²φ/∂z² = -ρω²(1-2p²V_S²)φ = ρω²S_zze^{ik_z^Pz}e^i(k_xx-ωt) σ_zx^P = 2μ∂²φ/∂z∂x = -2ρV_S²ωpk_zφ = ρω²S_zxe^{ik_z^Pz}e^i(k_xx-ωt)	S_zz = -(1-2p²V_S²) S_zx = 2V_S²pcosθ/V_P	S_zz = -(1-2p²V_S²)R_φ S_zx = -(2V_S²pcosθ/V_P)R_φ	.
contraintes exercées par onde SV sur une surface horizontale σ_zz^S = 2μ∂²ψ_y/∂z∂x = -2ρV_S²ωpk_zψ = ρω²S_zze^{ik_z^Sz}e^i(k_xx-ωt) σ_zx^S = μ(-∂²ψ_y/∂z²+∂²ψ_y/∂x²) = ρω²(1-2p²V_S²)ψ = ρω²S_zxe^{ik_z^Sz}e^i(k_xx-ωt)	.	.	S_zz = -(2V_S²pcosη/V_S)R_ψ S_zx = (1-2p²V_S²)R_ψ
onde P incidente, contraintes nulles sur surface libre z = 0 (σ_zz^PI + σ_zz^PR + σ_zz^SR)(z=0) = 0 (σ_zx^PI + σ_zx^PR + σ_zx^SR)(z=0) = 0	(1-2p²V_S²)(1+R_φ)+(2V_S²pcosη/V_S)R_ψ = 0 (2V_S²pcosθ/V_P)(1-R_φ)+(1-2p²V_S²)R_ψ = 0
légende reflps	D = (1-2p²V_S²)²+4V_S⁴p²cosθ/V_Pcosη/V_S R_φ = (-(1-2p²V_S²)²+4V_S⁴p²cosθ/V_Pcosη/V_S)/D R_ψ = (-4(1-2p²V_S²)V_S²pcosθ/V_P)/D
onde SV incidente, contraintes nulles sur surface libre z = 0 (σ_zz^SI + σ_zz^PR + σ_zz^SR)(z=0) = 0 (σ_zx^SI + σ_zx^PR + σ_zx^SR)(z=0) = 0	(1-2p²V_S²)R'_φ+(2V_S²pcosη/V_S)(-1+R'_ψ) = 0 -(2V_S²pcosθ/V_P)R'_φ+(1-2p²V_S²)(1+R'_ψ) = 0
légende reflps	R'_φ = (4(1-2p²V_S²)V_S²pcosη/V_S)/D R'_ψ = (-(1-2p²V_S²)²+4V_S⁴p²cosθ/V_Pcosη/V_S))/D
réflexion totale de l'onde SV , sinη > V_S/V_P (η > 36°) onde P réfléchie évanescente : k_z^P = iω(p²V_P²-1)^½/V_P	R'_ψ = e^iχ'(p) χ'(p) = -2Arctg((4V_S⁴p²(p²V_P²-1)^½/V_Pcosη/V_S)/(1-2p²V_S²)²)

loi de Snell : k_x = ωp = ωsinθ₁/V_P₁ = ωsinη₁/V_S₁ = ωsinθ₂/V_P₂ = ωsinη₂/V_S₂
P incidente descendante Φ^I = 1 k_z^I = ωcosθ₁/V_P1	P réfléchie montante Φ^R = R_φ k_z^P = -ωcosθ₁/V_P1	SV réfléchie montante Ψ^R = R_ψ k_z^S = -ωcosη₁/V_S1	P transmise descendante Φ^T = T_φ k_z^P = ωcosθ₂/V_P2	SV transmise descendante Ψ^T = T_ψ k_z^S = ωcosη₂/V_S2
U_x = p	+ pR_φ	+ (cosη₁/V_S1)R_ψ	= pT_φ	-(cosη₂/V_S2)T_ψ
U_z = cosθ₁/V_P1	-(cosθ₁/V_P1)R_φ	+ pR_ψ	= (cosθ₂/V_P2)T_φ	+ pT_ψ
S_zz = ρ₁(1-2p²V_S1²)	+ ρ₁(1-2p²V_S1²)R_φ	- (2ρ₁V_S1²pcosη₁/V_S1)R_ψ	= ρ₂(1-2p²V_S2²)T_φ	+ (2ρ₂V_S2²pcosη₂/V_S2)T_ψ
S_zx = -2ρ₁V_S1²pcosθ₁/V_P1	+ (2ρ₁V_S1²pcosθ₁/V_P1)R_φ	+ ρ₁(1-2p²V_S1²)R_ψ	= -(2ρ₂V_S2²pcosθ₂/V_P2)T_φ	+ ρ₂(1-2p²V_S2²)T_ψ
écriture matricielle cas liquide-solide	AR = B ; R = [R_φ , R_ψ , T_φ , T_ψ]^t ; B = [-p , -cosθ₁/V_P1 , -ρ₁(1-2p²V_S1²) , 2ρ₁V_S1²pcosθ₁/V_P1]^t A_LR_L = B_L ; R_L = [R_φ , T_φ , T_ψ]^t ; B_L = [-cosθ₁/V_P1 , -ρ₁ , 0]^t
A[4,4] A_L[3,3]	p	cosη₁/V_S1	-p	cosη₂/V_S2
	-cosθ₁/V_P1	p	-cosθ₂/V_P2	-p
	ρ₁(1-2p²V_S1²) (ρ₁)	-2ρ₁V_S1²pcosη₁/V_S1	-ρ₂(1-2p²V_S2²)	-2ρ₂V_S2²pcosη₂/V_S2
	2ρ₁V_S1²pcosθ₁/V_P1 (0)	ρ₁(1-2p²V_S1²)	2ρ₂V_S2²pcosθ₂/V_P2	-ρ₂(1-2p²V_S2²)
P incidente descendante ou montante légende reflpsv - reflpsv.m	R_φ = det([B,A[:,2:4]])/det(A) t_φ = det([b,A[:,2:4]])/det(A)	R_ψ = det([A[:,1],B,A[:,3:4]])/det(A) t_ψ = det([A[:,1],b,A[:,3:4]])/det(A)	T_φ = det([A[:,1:2],B,A[:,4]])/det(A) r_φ = det([A[:,1:2],b,A[:,4]])/det(A)	T_ψ = det([A[:,1:3],B])/det(A) r_ψ = det([A[:,1:3],b])/det(A)
P incidente descendante D = det(A) = P-Q R_φ = (-P-Q)/D R_ψ =2S/D	AR = B ; R = [R_φ , R_ψ , T_φ , T_ψ]^t ; B = [-p , -cosθ₁/V_P1 , -ρ₁(1-2p²V_S1²) , 2ρ₁V_S1²pcosθ₁/V_P1]^t = [-a₁₁ , a₂₁ , -a₃₁ , a₄₁]^t ; D = (a₁₁A₁₁+a₃₁A₃₁)-(a₂₁A₂₁+a₄₁A₄₁) ; DR_φ = -(a₁₁A₁₁+a₃₁A₃₁)-(a₂₁A₂₁+a₄₁A₄₁) DR_ψ/2 = a₁₁a₂₁(a₃₃a₄₄-a₄₃a₃₄) +a₁₁a₄₁(a₂₃a₃₄-a₃₃a₂₄) +a₃₁a₄₁(a₁₃a₂₄-a₂₃a₁₄) DT_φ/2 = -(a₁₁a₂₁(a₃₂a₄₄-a₄₂a₃₄) +a₁₁a₄₁(a₂₂a₃₄-a₃₂a₂₄) +a₃₁a₄₁(a₁₂a₂₄-a₂₂a₁₄)) DT_ψ/2 = (a₁₁a₂₁(a₃₂a₄₃-a₄₂a₃₃) +a₁₁a₄₁(a₂₂a₃₃-a₃₂a₂₃) +a₃₁a₄₁(a₁₂a₂₃-a₂₂a₁₃)
P incidente montante k_z^I = -ωcosθ₂/V_P2	Ar = b ; r = [t^φ,t^ψ,r^φ,r^ψ]^t b = [p , -cosθ₂/V_P2 , ρ₂(1-2p²V_S2²) , 2ρ₂V_S2²pcosθ₂/V_P2]^t = [-a₁₃ , a₂₃ , -a₃₃ , a₄₃]^t D = (a₁₃A₁₃+a₃₃A₃₃)-(a₂₃A₂₃+a₄₃A₄₃) ; Dr_φ = -(a₁₃A₁₃+a₃₃A₃₃)-(a₂₃A₂₃+a₄₃A₄₃) Dr_ψ/2 = a₁₃a₂₃(a₃₁a₄₂-a₄₁a₃₂) +a₁₃a₄₃(a₂₁a₃₂-a₃₁a₂₂) +a₃₃a₄₃(a₁₁a₂₂-a₂₁a₁₂) Dt_φ/2 = -(a₁₃a₂₃(a₃₄a₄₂-a₄₄a₃₂) +a₁₃a₄₃(a₂₄a₃₂-a₃₄a₂₂) +a₃₃a₄₃(a₁₄a₂₂-a₂₄a₁₂)) Dt_ψ/2 = a₁₃a₂₃(a₃₄a₄₁-a₄₄a₃₁) +a₁₃a₄₃(a₂₄a₃₁-a₃₄a₂₁) +a₃₃a₄₃(a₁₄a₂₁-a₂₄a₁₁)
cas liquide-solide reflpsl.m	A_LR_L = B_L ; R_L = [R_φL , T_φL , T_ψL]^t ; B_L = [-cosθ₁/V_P1 , -ρ₁ , 0]^t A_Lr_L = b_L ; r_L = [t_φL , r_φL , r_ψL]^t ; b_L = [-cosθ₂/V_P2 , ρ₂(1-2p²V_S2²) , 2ρ₂V_S2²pcosθ₂/V_P2]^t D_L = -ρ₂²cosθ₁/V_P1((1-2p²V_S2²)²+4V_S2⁴p²cosθ₂/V_P2cosη₂/V_S2) -ρ₁ρ₂cosθ₂/V_P2 D_LR_φL = -ρ₂²cosθ₁/V_P1((1-2p²V_S2²)²+4V_S2⁴p²cosθ₂/V_P2cosη₂/V_S2) +ρ₁ρ₂cosθ₂/V_P2 D_LT_φL = -2ρ₁ρ₂cosθ₁/V_P1(1-2p²V_S2²) ; D_Lt_φL = -2ρ₂²cosθ₂/V_P2(1-2p²V_S2²) D_LT_ψL = -4ρ₁ρ₂cosθ₁/V_P1V_S2²pcosθ₂/V_P2
SV incidente descendante ou montante reflpsv.m	R'_φ = det([B',A[:,2:4]])/D t'_φ = det([b',A[:,2:4]])/D	R'_ψ = det([A[:,1],B',A[:,3:4]])/D t'_ψ = det([A[:,1],b',A[:,3:4]])/D	T'_φ = det([A[:,1:2],B',A[:,4]])/D r'_φ = det([A[:,1:2],b',A[:,4]])/D	T'_ψ = det([A[:,1:3],B'])/D r'_ψ = det([A[:,1:3],b'])/D
SV incidente descendante Ψ^I = 1 ; k_z^I = ωcosη₁/V_S1 D = det(A) = -P'+Q' R'_ψ = (-P'-Q')/D	AR'=B' ; R' = [R'_φ , R'_ψ , T'_φ , T'_ψ]^t ; B' = [cosη₁/V_S1 , -p , -2ρ₁V_S1²pcosη₁/V_S1 , -ρ₁(1-2p²V_S1²)]^t = [a₁₂ , -a₂₂ , a₃₂ , -a₄₂]^t ; D = -(a₁₂A₁₂+a₃₂A₃₂)+(a₂₂A₂₂+a₄₂A₄₂) ; DR'_ψ = -(a₁₂A₁₂+a₃₂A₃₂)-(a₂₂A₂₂+a₄₂A₄₂)
SV incidente montante k_z^I = -ωcosη₂/V_S2	Ar'=b' ; r' = [t'_φ , t'_ψ , r'_φ , r'_ψ]^t b' = [cosη₂/V_S2 , p , -2ρ₂V_S2²pcosη₂/V_S2 , ρ₂(1-2p²V_S2²)]^t = [a₁₄ , -a₂₄ , a₃₄ , -a₄₄]^t ; D = -(a₁₄A₁₄+a₃₄A₃₄)+(a₂₄A₂₄+a₄₄A₄₄) Dr'_ψ = -(a₁₄A₁₄+a₃₄A₃₄)-(a₂₄A₂₄+a₄₄A₄₄)
réflexion totale de l'onde SV descendante p = sinη₁/V_S₁ 1/V_S1 > p > 1/V_P1 p > 1/V_S2 > 1/V_P2 R'_ψ = e^iχ'(p)	termes de A imaginaires : a₁₄ = i(p²V_S2²-1)^½/V_S2 ; a₂₁ = -i(p²V_P1²-1)^½/V_P1 ; a₂₃ = -i(p²V_P2²-1)^½/V_P2 ; a₃₄ = -2iρ₂V_S2²p(p²V_S2²-1)^½/V_S2 ; a₄₁ = 2iρ₁V_S1²p(p²V_P1²-1)^½/V_P1 ; a₄₃ = 2iρ₂V_S2²p(p²V_P2²-1)^½/V_P2 ; ⇒ A₁₂, A₃₂ et P' sont imaginaires purs, A₁₂, A₃₂ et Q' sont réels R'_ψ = (-P'-Q')/(-P'+Q') = e^iχ'(p) χ'(p) = 2Arctg(P'/iQ') = 2Arctg((1/i)(a₁₂A₁₂+a₃₂A₃₂)/(a₂₂A₂₂+a₄₂A₄₂))

JMM ex EOST : Ondes sismiques - Imagerie - Traitement

Rayons, distances et temps de propagation pour V(z) - VRMS : stratification - gradient de vitesse - gradient et couches

Rayons, fronts d'onde, amplitude pour V(x,y,z) : pendage - rayons 3D

Anisotropie (cas isotrope transverse) : milieu équivalent - propagation

Rayons, distances et temps de propagation pour V(z) - V_RMS : stratification - gradient de vitesse - gradient et couches

faibles contrastes	ρ₂ = ρ+δρ ; V_P₂ = V_P+δV_P ; θ₂ = θ+δθ ; δθ = tgθδV_P/V_P ; V_S₂ = V_S+δV_S ; η₂ = η + δη ; δη = tgηδV_S/V_S a₁₁ = -a₁₃ = a₂₂ = -a₂₄ = p ; a₁₂ = cosη/V_S ; a₂₁ = -cosθ/V_P ; a₃₁ = a₄₂ = ρ(1-2p²V_S²) ; a₃₂ = -2ρV_S²pcosη/V_S ; a₄₁ = 2ρV_S²pcosθ/V_P a₁₄ = (a₁₂+δa₁₂) ; a₂₃ = (a₂₁+δa₂₁) ; a₃₃ = a₄₄ = -(a₃₁+δa₃₁) ; a₃₄ = (a₃₂+δa₃₂) ; a₄₃ = (a₄₁+δa₄₁)
D = det(A)	D = (p²-a₂₁a₁₂)(a₃₁²-a₄₁a₃₂) - (2pa₂₁)(-2a₃₁a₃₂) + (-p²-a₂₁a₁₂)(a₃₂a₄₁+a₃₁²) + (a₁₂a₂₁+p²)(-a₃₁²-a₄₁a₃₂) - (-2pa₁₂)(2a₃₁a₄₁) + (p²-a₂₁a₁₂)(a₃₁²-a₄₁a₃₂) D = 2(p²-a₂₁a₁₂)(a₃₁²-a₄₁a₃₂) -2(p²+a₂₁a₁₂)(a₃₂a₄₁+a₃₁²) +4pa₃₁(a₂₁a₃₂+a₁₂a₄₁) = -4p²a₄₁a₃₂ -4a₂₁a₁₂a₃₁² +4pa₃₁(a₂₁a₃₂+a₁₂a₄₁) D = 4cosθ/V_Pcosη/V_S [p²(2ρV_S²p)² +(ρ(1-2p²V_S²))² +4ρ²p²V_S²(1-2p²V_S²)] = 4ρ²cosθ/V_Pcosη/V_S
R_φ	DR_φ = (-p²-a₂₁a₁₂)((a₃₁+δa₃₁)²-(a₄₁+δa₄₁)(a₃₂+δa₃₂)) - (-p(a₂₁+δa₂₁)+pa₂₁)(-a₃₂(a₃₁+δa₃₁)-a₃₁(a₃₂+δa₃₂)) + (p²-a₂₁(a₁₂+δa₁₂))(a₃₂(a₄₁+δa₄₁)+a₃₁(a₃₁+δa₃₁)) + (a₁₂(a₂₁+δa₂₁)+p²)(a₃₁(a₃₁+δa₃₁)-a₄₁(a₃₂+δa₃₂)) - (-pa₁₂-p(a₁₂+δa₁₂))(-a₃₁(a₄₁+δa₄₁)+a₄₁(a₃₁+δa₃₁)) + (p²-(a₂₁+δa₂₁)(a₁₂+δa₁₂))(-a₃₁²-a₄₁a₃₂)) DR_φ = (-p²-a₂₁a₁₂)(2a₃₁δa₃₁-a₄₁δa₃₂-a₃₂δa₄₁) - 2pa₃₂a₃₁δa₂₁ + (p²-a₂₁a₁₂)(a₃₂δa₄₁+a₃₁δa₃₁)-a₂₁δa₁₂(a₃₂a₄₁+a₃₁²) + (p²+a₁₂a₂₁)(a₃₁δa₃₁-a₄₁δa₃₂)+a₁₂δa₂₁(a₃₁²-a₄₁a₃₂) + 2pa₁₂(-a₃₁δa₄₁+a₄₁δa₃₁) + (a₂₁δa₁₂+a₁₂δa₂₁)(a₃₁²+a₄₁a₃₂) DR_φ = 2(p(pa₃₂-a₁₂a₃₁)δa₄₁ + a₁₂(pa₄₁-a₂₁a₃₁)δa₃₁ + a₃₁(a₃₁a₁₂-pa₃₂)δa₂₁) DR_φ = 2ρ(-2p²cosη/V_Sδ(ρV_S²cosθ/V_P) +cosη/V_Scosθ/V_Pδ(ρ(1-2p²V_S²) + ρ(1-2p²V_S²)cosη/V_Sδ(-cosθ/V_P)) DR_φ = 2ρcosη/V_S(cosθ/V_P((1-4p²V_S²)δρ - 4ρp²δ(V_S²)) - ρδ(cosθ/V_P)) R_φ = (1/2)((1-4p²V_S²)δρ/ρ - 8p²V_S²δV_S/V_S - δ(cosθ/V_P)/(cosθ/V_P)) R_φ = (1/2)((1-4p²V_S²)δρ/ρ - 8p²V_S²δV_S/V_S + (1/cosθ)²δV_P/V_P) R_φ = (1/2)((δρ/ρ+δV_P/V_P) + (δV_P/V_P -4V_S²/V_P²(δρ/ρ+2δV_S/V_S)sin²θ + (tg²θ-sin²θ)δV_P/V_P) ≈ R₀+Gsin²θ
R_ψ	DR_ψ = (2pa₂₁)((a₃₁+δa₃₁)²-(a₄₁+δa₄₁)(a₃₂+δa₃₂)) - p((a₂₁+δa₂₁)+a₂₁)(a₃₁(a₃₁+δa₃₁)-a₄₁(a₃₂+δa₃₂)) + (-p²-a₂₁(a₁₂+δa₁₂))(-a₃₁(a₄₁+δa₄₁)+a₄₁(a₃₁+δa₃₁)) + p(-(a₂₁+δa₂₁)+a₂₁)(-a₃₁(a₃₁+δa₃₁)-a₄₁(a₃₂+δa₃₂)) - (p²-a₂₁(a₁₂+δa₁₂))(a₃₁(a₄₁+δa₄₁)+a₄₁(a₃₁+δa₃₁)) + (p²-(a₂₁+δa₂₁)(a₁₂+δa₁₂))(2a₃₁a₄₁) DR_ψ = 2pa₂₁(2a₃₁δa₃₁-a₄₁δa₃₂-a₃₂δa₄₁) - 2pa₂₁(a₃₁δa₃₁-a₄₁δa₃₂)-pδa₂₁(a₃₁²-a₄₁a₃₂) + (-p²-a₂₁a₁₂)(-a₃₁δa₄₁)+a₄₁δa₃₁)) + (-pδa₂₁)(-a₃₁²-a₄₁a₃₂) - (p²-a₂₁a₁₂)(a₃₁δa₄₁+a₄₁δa₃₁) +a₂₁δa₁₂2a₃₁a₄₁ + (-2a₃₁a₄₁(a₂₁δa₁₂+a₁₂δa₂₁)) DR_ψ = 2(p(a₂₁a₃₁-pa₄₁)δa₃₁ + a₂₁(-pa₃₂+a₁₂a₃₁)δa₄₁ + a₄₁(pa₃₂-a₃₁a₁₂)δa₂₁) DR_ψ = -2ρpcosθ/V_P(δ(ρ(1-2p²V_S²)) + cosη/V_Sδ(2ρV_S²cosθ/V_P) + 2ρV_S²cosη/V_Sδ(-cosθ/V_P)) DR_ψ = -2ρpcosθ/V_P ((1-2p²V_S²+2V_S²cosθ/V_Pcosη/V_S)δρ + 2ρ(-p²+cosη/V_Scosθ/V_P)δ(V_S²) R_ψ = -(1/2)pV_S/cosη ((1-2p²V_S²+2V_S²cosθ/V_Pcosη/V_S)δρ/ρ + 4V_S²(-p²+cosη/V_Scosθ/V_P)δV_S/V_S) R_ψ ≈ -(1/2)sinη ((1+2V_S/V_P)δρ/ρ + 4V_S/V_PδV_S/V_S) pour incidence faible

1/V_R = p = k_x/ω > 1/V_S > 1/V_P	onde P évanescente k_z^P = iω(p²V_P²-1)^½/V_P	onde S évanescente k_z^S = iω(p²V_S²-1)^½/V_S
σ_zz = σ_zx = 0 sur surface libre z = 0	(1-2p²V_S²)Φ+i2pV_S(p²V_S²-1)^½Ψ = 0 -i2V_S²p(p²V_P²-1)^½/V_PΦ+(1-2p²V_S²)Ψ = 0
légende rayleq	déterminant = 0 (1-2p²V_S²)²-4p²V_S⁴(p²V_S²-1)^½/V_S(p²V_P²-1)^½/V_P = 0 (2-V_R²/V_S²)²-4(1-V_R²/V_P²)^½(1-V_R²/V_S²)^½ = 0 (V_R²/V_S²)³-8(V_R²/V_S²)²+4(6-4V_S²/V_P²)V_R²/V_S²+16(V_S²/V_P²-1) = 0	solutions réelles de x³+bx²+cx+d = 0 A = (3c-b²)/9 ; B = (9bc-27d-2b³)/54 ; Δ = A³+B² si Δ > 0 , C³ = B+Δ^½ ; D³ = B-Δ^½ ; x = C+D-b/3 si Δ = 0, x = 2B^⅓-b/3 ; x = -B^⅓-b/3 si Δ < 0 , θ = arccos(B/(-A³)^½) ; x = 2(-A)^½cos((θ+2nπ)/3)-b/3 avec n = 0,1,2
légende rayleigh (u_x , u_z) = (U_x(z) , U_z(z))e^iω(x/V_R-t)	U_x = iωpΦe^{-ωz(p²V_P²-1)^½/V_P}+ω(p²V_S²-1)^½/V_SΨe^{-ωz(p²V_S²-1)^½/V_S} U_z = -ω(p²V_P²-1)^½/V_PΦe^{-ωz(p²V_P²-1)^½/V_P}+iωpΨe^{-ωz(p²V_S²-1)^½/V_S} U_x = e^iπ/2ωpΦ(e^{-ωz(p²V_P²-1)^½/V_P}+(1/(2p²V_S²)-1)e^{-ωz(p²V_S²-1)^½/V_S}) U_z = e^iπω(p²V_P²-1)^½/V_PΦ(e^{-ωz(p²V_P²-1)^½/V_P}+(1/(2p²V_S²)-1)^-1e^{-ωz(p²V_S²-1)^½/V_S})

légende love	onde stationnaire en z k_z pour modes propres	onde progressive en x , k_x = (ω²/V_S²-k_z²)^½ vitesse de phase V(ω) = V_ax = ω/k_x	ω ≥ fréquence de coupure ω_c k_x réel pour onde progressive en x
modes propres 1D do, do, sol, do, mi, sol...	e^ikz+e^-ikz = 2cos(kz) Hk_n = nπ , nλ_n/2 = H , n = 1,2,3...
plaque à bords libres R_sup = R_inf = 1	e^ik_zz+e^-ik_zz = 2cos(k_zz) Hk_{z n} = nπ , nλ_{z n}/2 = H , n = 1,2,3...	k_{x n} = (ω²/V_S²-(nπ/H)²)^½ V_n(ω) = ω/k_{x n}	ω_{c n} = nπV_S/H
couche (-H ≤ z ≤ 0) sur 1/2 espace (z≥ 0) R_surf = 1 ; R_interf = e^iχ(p)	e^ik_1zz+e^iχ(p)e^-ik_1zz = 2e^iχ(p)/2cos(k_1zz-χ(p)/2) Hk_{1z n}+χ(p)/2 = nπ , n = 0,1,2,3...	k_{x n} = (ω²/V_S1²-(nπ-χ(p)/2)²/H²)^½ V_{L n}(ω) = ω/k_{x n} = 1/p_n	k_{x nc} = ω_{c n}/V_S2 ; χ(1/V_S2) = 0 ω_{c n} = nπ/(H(1/V_S1²-1/V_S2²)^½)
légende lovdisp - displov.m	k_1z = (ω/V_S1)(1-p²V_S1²)^½ χ(p) = -2Arctg(ρ₂V_S2(p²V_S2²-1)^½/ρ₁V_S1(1-p²V_S1²)^½) = -2Arctg(I₂/I₁) relation de dispersion de l'onde de Love : ω(p_n) = (-χ(p_n)/2+nπ)V_S1/(H(1-p_n²V_S1²)^½) = (Arctg(I₂/I₁)+nπ)V_S1/(H(1-p_n²V_S1²)^½)

conditions aux limites	modes propres en z	onde progressive en x	fréquence de coupure
R_surf = e^iχ'₁(p) R_interf = e^iχ'₂(p) χ'₁₂(p) = χ'₁(p)+χ'₂(p)	(n-χ'₁₂(p)/2π)λ_{1z n}/2 = H Hk_{1z n}+χ'₁₂(p)/2 = nπ	k_{x n} = (ω²/V_S1²-(nπ-χ'₁₂(p)/2)²/H²)^½ V_{R n}(ω) = ω/k_{x n} = 1/p_n	ω_{c n} = (nπ-χ'₁₂(1/V_S2))/2)/(H(1/V_S1²-1/V_S2²)^½)
rel. dispersion Rayleigh harmoniques n≥1 V_S1≤V_{R n}≤V_S2	χ'₁(p) = -2Arctg((4V_S1⁴p²(p²V_P1²-1)^½/V_P1(1-p²V_S1²)^½/V_S1)/(1-2p²V_S1²)²) = -2Arctg(S) χ'₂(p) = -2Arctg(Im(D)/Re(D)) = -2Arctg(I) tg(Hω(1-p²V_S1²)^½/V_S1) = -tg((χ'₁(p)+χ'₂(p))/2) = (I+S)/(1-IS) ω(p_n) = (-(χ'₁(p_n)+χ'₂(p_n))/2+nπ)V_S1/(H(1-p_n²V_S1²)^½) = (Arctg((I+S)/(1-IS))+nπ)V_S1/(H(1-p_n²V_S1²)^½)

cond. limites	descendante P1 , k_zP1 = ω(1-p²V_P1²)^½/V_P1 Z_P1 = e^-ik_zP1H	descendante S1 , k_zS1 = ω(1-p²V_S1²)^½/V_S1 Z_S1 = e^-ik_zS1H	montante P1 , -k_zP1	montante S1 , -k_zS1	évanescente P2 , k_zP2 = iω(p²V_P2²-1)^½/V_P2	évanescente S2 , k_zS2 = iω(p²V_S2²-1)^½/V_S2
z = -H	σ_zz(k_zP1²)Z_P1	-2μ₁k_xk_zS1Z_S1	σ_zz(k_zP1²)/Z_P1	2μ₁k_xk_zS1/Z_S1	0	0
z = -H	-2μ₁k_xk_zP1Z_P1	σ_zx(k_zS1²)Z_S1	2μ₁k_xk_zP1/Z_P1	σ_zx(k_zS1²)/Z_S1	0	0
z = 0	k_x	-k_zS1	k_x	k_zS1	-k_x	k_zS2
	k_zP1	k_x	-k_zP1	k_x	-k_zP2	-k_x
	σ_zz(k_zP1²)	-2μ₁k_xk_zS1	σ_zz(k_zP1²)	2μ₁k_xk_zS1	-σ_zz(k_zP2²)	2μ₂k_xk_zS2
	-2μ₁k_xk_zP1	σ_zx(k_zS1²)	2μ₁k_xk_zP1	σ_zx(k_zS1²)	2μ₂k_xk_zP2	-σ_zx(k_zS2²)

cond. lim.	ondes guidées par surf.libre en z = -H et prolongées en z = 0 par Z_P1 = e^{-ω(p²V_P1²-1)^½/V_P1H} (0) ; Z_S1 = e^{-ω(p²V_S1²-1)^½/V_S1H} (0)		ondes guidées par interf. en z = 0 et prolongées en z = -H par Z_P1 , Z_S1
z = -H	Rayleigh surf. libre		(1-2p²V_S1²)Z_P1 (0)	-i2pV_S1(p²V_S1²-1)^½Z_S1 (0)	0	0
z = -H	Rayleigh surf. libre		+i2V_S1²p(p²V_P1²-1)^½/V_P1Z_P1 (0)	+(1-2p²V_S1²)Z_S1 (0)	0	0
z = 0	pZ_P1 (0)	-i(p²V_S1²-1)^½/V_S1Z_S1 (0)	Stoneley à l'interface
	i(p²V_P1²-1)^½/V_P1Z_P1 (0)	pZ_S1 (0)
	ρ₁(1-2p²V_S1²)Z_P1 (0)	i2ρ₁V_S1²p(p²V_S1²-1)^½/V_S1Z_S1 (0)
	-i2ρ₁V_S1²p(p²V_P1²-1)^½/V_P1Z_P1 (0)	ρ₁(1-2p²V_S1²)Z_S1 (0)

z I_i = ρ_iV_Si²k_iz	onde descendante e^k_izz k_iz = ω(1/V_Si²-p²)^½	onde montante e^-ik_izz	continuité u_y et σ_yz à l'interface réflexion totale si surface libre (montante = descendante) relation de dispersion basse fréquence	onde descendante e^k_izz R₂₁ = (I₂-I₁)/(I₂+I₁) T₂₁ = 2I₂/(I₂+I₁)	onde montante e^-ik_izz T₁₂ = 2I₁/(I₂+I₁) R₁₂ = -R₂₁	T₂₁ = 1+R₂₁ T₁₂ = 1+R₁₂ = 1-R₂₁ T₁₂T₂₁-R₁₂R₂₁ = 1
-(h₃+h₂+h₁) couche 3	D₃e^-ik_3zh₃ = D₃(a₃-ib₃)	M₃e^ik_3zh₃ = M₃(a₃+ib₃)	A₃b₃+a₃B₃ = 0 tg(k_3zh₃)+(I₂/I₃)tg(k_2zh₂)+((I₁/I₃)-(I₁/I₂)tg(k_3zh₃)tg(k_2zh₂))tg(k_1zh₁+χ/2) = 0
-(h₂+h₁) couche 3	D₃ = A₃-iB₃	M₃ = A₃+iB₃	A₃ = A₂a₂-B₂b₂ = a₁a₂-(I₁/I₂)b₁b₂ B₃ = (I₂/I₃)(A₂b₂+B₂a₂) = (I₂/I₃)a₁b₂+(I₁/I₃)b₁a₂
-(h₂+h₁) couche 2	D₂e^-ik_2zh₂ = D₂(a₂-ib₂)	M₂e^ik_2zh₂ = M₂(a₂+ib₂)	A₂b₂+a₂B₂ = 0 tg(k_2zh₂)+(I₁/I₂)tg(k_1zh₁+χ/2) = 0	1	1	(1-R₁₀R₁₂e^i2k_1zh₁)(1 - R₂₁e^i2k_2zh₂) = T₁₂ R₁₀T₂₁e^{i2(k_2zh₂+k_1zh₁)} (e^-i2k_1zh₁-R₁₀R₁₂)(e^-i2k_2zh₂ - R₂₁) = T₁₂ R₁₀T₂₁ e^{-i2(k_2zh₂+k_1zh₁)}+R₂₁(R₁₀e^-i2k_2zh₂-e^-i2k_1zh₁) = R₁₀
-h₁ couche 2	D₂ = A₂-iB₂	M₂ = A₂+iB₂	A₂ = a₁ B₂ = (I₁/I₂)b₁	e^ik_2zh₂	e^-ik_2zh₂ = R₂₁e^ik_2zh₂+T₁₂Me^ik_1zh₁	M = (e^-ik_2zh₂ - R₂₁e^ik_2zh₂)e^-ik_1zh₁/T₁₂
-h₁ couche 1	D₁e^-ik_1zh₁ = a₁-ib₁	M₁e^ik_1zh₁ = a₁+ib₁	b₁ = 0 sin(k_1zh₁+χ/2) = 0	onde stationnaire si k_1z réel, évanescente si k_1z imaginaire
0 couche 1	D₁ = e^-iχ/2	M₁ = e^iχ/2	χ(p) = -2Arctg(ρV_S(p²V_S²-1)^½/ρ₁V_S1(1-p²V_S1²)^½) = -2Arctg(I/I₁)	D = T₂₁e^{i(k_2zh₂+k_1zh₁})+R₁₂Me^i2k_1zh₁	M = R₁₀D = (I₁-I₀)D/(I₁+I₀)	M = R₁₀T₂₁e^{i(k_2zh₂+k_1zh₁})/(1-R₁₀R₁₂e^i2k_1zh₁)
> 0 1/2 espace	onde évanescente e^-k_zz k_z = \|ω\|(p²-1/V²)^½			onde évanescente e^-k_zz k_z = \|ω\|(p²-1/V²)^½

eq. de Bessel	solution	dérivation
r²d²f/dr²+rdf/dr+ (k_r²r²-n²)f(r) = 0	f(r) = H_n(k_rr) = J_n(k_rr)+iY_n(k_rr) ≈ (2/πk_rr)^½e^{i(k_rr-π/4-nπ/2)} H_n(ik_rr) ≈ i^-(n+1)(2/πk_rr)^½e^-k_rr	dH_n(k_rr)/dr = k_rH_n-1(k_rr)-(n/r)H_n(k_rr) = (n/r)H_n(k_rr)-k_rH_n+1(k_rr)

Δφ(r,z) = ∂²φ/∂r²+(1/r)∂φ/∂r+∂²φ/∂z² = (1/V_P²)∂²φ/∂t²	φ(r,z) = f(r)e^i(k_zz-ωt)	k_p² = ω²/V_P²-k_z²	f(r) = AH₀(k_pr)
Δψ_θ(r,z) = (1/V_S²)∂²ψ_θ/∂t²	ψ_θ(r,z) = g(r)e^i(k_zz-ωt)	k_s² = ω²/V_S²-k_z²	g(r) = BH₁(k_sr)

Δφ(r,θ,z) = Δφ(r,z) + (1/r)²∂²φ/∂θ² = (1/V_P²)∂²φ/∂t²	φ(r,θ,z) =f(r)cos(nθ)e^i(k_zz-ωt)	k_p² = ω²/V_P²-k_z²	f(r) = AH_n(k_pr)
Δψ_r(r,θ,z) = (1/V_S²)∂²ψ_r/∂t²	ψ_r(r,z) = g(r)sin(nθ)e^i(k_zz-ωt)	k_s² = ω²/V_S²-k_z²	g(r) = BH_n+1(k_sr)
Δψ_θ(r,θ,z) = (1/V_S²)∂²ψ_θ/∂t²	ψ_θ(r,z) = -g(r)cos(nθ)e^i(k_zz-ωt)		g(r) = BH_n+1(k_sr)
Δψ_z(r,θ,z) = (1/V_S²)∂²ψ_z/∂t²	ψ_z(r,z) = h(r)sin(nθ)e^i(k_zz-ωt)		h(r) = CH_n(k_sr)