Vérifier que le temps d’arrivée t0 = 0.81 s de l’onde réfléchie en X = 0 correspond à une valeur du gradient de vitesse a = 1 /s dans la couche (Rappel : il faut intégrer le temps de trajet vertical dans la couche)
Déterminer la valeur pm du paramètre du rayon émergeant au point entouré par un carré puis calculer la distance Xm et le temps Tm correspondant (Rappel : les rayons sont des cercles centrés en z = -V1/a)
Déterminer la valeur pc du paramètre du rayon émergeant au point entouré par un cercle puis calculer la distance Xc et le temps Tc correspondant.
Dessiner dans le plan (x,z) les rayons qui émergent aux déports suivants : a) X = 1000 m , b) X = 2000 m , c) X = 4000 m
Examen 2015
Soit une onde harmonique de type SH, de pulsation ω = 2πf, se propageant dans le plan (x,z), dans un milieu de vitesse VS1 et masse volumique ρ1, avec un angle d’incidence η1 par rapport à l’axe z.Le déplacement des particules s’écrit : uy(x,z,t) = Uy exp(ikzz)exp(i(kxx-ωt) ) où exp est la fonction exponentielle.
Ecrire l’expression de kx et kz en fonction de ω, η1 et VS1 pour une onde se propageant vers les x et z croissant.
L’onde se réfléchit sur une interface plane située en z = 0 entre deux demi-espaces de vitesses VS1 et VS2 et masses volumiques ρ1 et ρ2
Ecrire les déplacements des particules pour les ondes réfléchie et transmise en spécifiant kx et kz pour chaque onde.
Ecrire la continuité du déplacement des particules sur l’interface en z = 0.
Ecrire la continuité de la contrainte qui s’applique sur l’interface z = 0.
Déterminer l’expression du coefficient de réflexion R sur l’interface.
On suppose que VS2 > VS1 et que le paramètre p > 1/ VS2 ,
Exprimer R(p).
Déterminer la valeur du déphasage χ(p) à la réflexion.
Montrer que la somme des ondes incidente et réfléchie produit une onde stationnaire selon z.
Déterminer les valeurs de z pour lesquelles il existe un ventre de vibration.
Ecrire la condition d’interférence constructive pour des ondes harmoniques SH totalement réfléchies dans une couche de vitesse VS1 et épaisseur H
surmontant un demi-espace de vitesse VS2 > VS1
Donner l’expression de la relation de dispersion ω(p) pour l’onde de Love guidée dans la couche avec une vitesse de phase VL(ω) = 1/p
Expliquer pourquoi VS1 < VL(ω) < VS2
Expliquer pourquoi VL(ω) est une fonction décroissante de la fréquence.
Contrôle continu 2015
Soit une onde P plane sinusoïdale se propageant dans un milieu de vitesse de propagation VP = 5000 m/s dans une direction
e (ex = cosα , ey = cosβ , ez = cosγ).
La figure représente les 3 composantes Ux, Uy et Uz du déplacement des particules sur des récepteurs alignés dans trois directions orthogonales Z, X et Y à un temps T fixé.
Exprimer les longueurs d’onde apparentes λax, λay, λaz en fonction de la longueur d’onde λ et des composantes de e.
Pour les récepteurs alignés le long de Y, on observe une longueur d’onde λay infinie. En déduire quel est le plan de propagation de l’onde P.
Pour les récepteurs alignés le long de Z, on mesure λaz = 577 m. Mesurer λax. En déduire la valeur de γ
Déterminer la longueur d’onde λ et la fréquence f sachant que VP = 5000 m/s.
Exprimer les valeurs maximum de Ux, Uy et Uz en fonction de la valeur maximum U du déplacement dans la direction e et des composantes de e.
Mesurer les valeurs maximum de Ux et Uz sur la figure. Vérifier que le rapport Ux / Uz donne la même valeur de γ que celle obtenue en 4). En déduire U.
La vitesse de propagation des ondes S dans le milieu est VS = 3000 m/s.
Déterminer la longueur d’onde λS pour une onde plane S sinusoïdale de même fréquence f que celle de l’onde P précédente.
Dessiner sur la figure les composantes de déplacement Ux, Uy et Uz pour une onde SH se propageant dans la même direction e que celle de l’onde P précédente en respectant les valeurs de longueurs d’onde apparentes pour l’onde SH. Prendre une valeur maximum arbitraire de déplacement égale à 0.01.
Soit une couche d’épaisseur d = 100 m et vitesse V1 = 1000 m/s sur un demi-espace de vitesse V2 = 2000 m/s. Une source ponctuelle et des récepteurs sont placés à la surface de la couche.
Déterminer :
la valeur de l’angle d’incidence critique θc mesuré par rapport à la verticale.
la distance source-récepteur Xc correspondant à l’émergence en surface de l’onde conique
la distance source-récepteur X1 à partir de laquelle l’onde conique arrive en première arrivée
Calculer :
les temps d’arrivée des ondes arrivant en X = 50 m, X = 200 m et X = 1000 m.
les vitesses apparentes horizontales de ces ondes (inverses des pentes des courbes T(X), fonction de l’angle d’émergence des rayons en surface)
Soit une couche d’épaisseur d = 1000 m et vitesse V(z) = V0 + az avec V0 = 1000 m/s et a = 1 /s sur un demi-espace de vitesse V2 = 2000 m/s (donc V(d) = V2).
Une source ponctuelle et des récepteurs sont placés à la surface de la couche.
Expliquer pourquoi il existe une distance source-récepteur maximum Xm pour l’arrivée en surface de l’onde.
Calculer Xm (rappel : les rayons sismiques sont des arcs de cercle de rayon R = 1/(ap) centrés en –V0/a au dessus de la surface).
Calculer Tm , temps d’arrivée en X = Xm (rappel : la primitive de 1/sinθ est ln(tg(θ/2)) )
Dessiner l’hodochrone T(X) en respectant la variation de pente en fonction de X et indiquer les valeurs de pente en X = 0 et X = Xm
Dans le modèle précédent la vitesse dans le demi-espace est V2 = 4000 m/s.
Le milieu 1 est maintenant une couche d’épaisseur H = 100 m entre une surface libre et l’interface avec le milieu 2.
L’onde de Rayleigh guidée à la vitesse VR par la surface libre (z = 0) d’un demi-espace élastique homogène de vitesses VP et VS peut être considérée comme
la somme de deux ondes évanescentes P et SV dont les potentiels du déplacement des particules sont :
Soit un milieu anisotrope homogène ayant un axe de symétrie vertical (isotropie transverse).
Les contraintes de cisaillement sont σxy = 2aεxy et σyz = 2bεyz où a = c66 et b = c44
Soit un milieu stratifié comportant une couche de vitesse V1 et épaisseur d1 sur une couche de vitesse V2 et épaisseur d2 surmontant un milieu de vitesse V3.
On suppose V1
Soit un milieu stratifié comportant une couche de vitesse V(z) = V0+az (a constant positif) et épaisseur d sur un milieu homogène de vitesse V2.
On suppose V0 < V1 = V(d) < V2.
Soit un milieu dans lequel la vitesse de propagation est V(x,y,z). Un front d’onde d’équation t = T(x,y,z) se propage dans le milieu. Soit e = gradT la direction de propagation de l’onde en un point M.
Pour pouvoir dessiner les fronts d’onde transmis (non sphériques), il est nécessaire de déterminer la géométrie des rayons transmis. On se contente d’un seul :
Expliquer en quoi l’hodochrone serait différent si l’interface présentait un pendage α.
I) Réflexion sur une couche d’épaisseur h et vitesse V à l’intérieur d’un espace homogène de vitesse V0.
II) Onde de Love guidée dans une couche d’épaisseur h et vitesse V entre une surface libre et un demi-espace de vitesse V0 > V.
III) Relation entre les ondes montantes et descendantes au sommet et à la base d’une couche d’épaisseur hi de vitesse Vi.
Le coefficient de réflexion sur l’interface Vi+1 / Vi est noté Ri .
Les déplacements des ondes montantes et descendantes à la base de la couche i sont notés Mi et Di.
IV) Onde de Love en milieu stratifié
Vérifier que la première arrivée est l’arrivée directe dans l’eau et estimer la profondeur d’eau H0.
On veut maintenant exploiter le fait que l’on a des capteurs 3 composantes pour déterminer les propriétés des sédiments.
On note ρ0 et V0 la densité et la vitesse de propagation dans l’eau, ρ ,VP et VS la densité et les vitesses de propagation des ondes P et S dans les sédiments.
On suppose VS < V0 < VP . On note θ0, θ, η les angles d’incidence des ondes par rapport à la verticale et p = sin θ0/V0.
L’axe z est orienté vers le bas et l’interface eau-sédiment est le plan z = 0.
La couche sédimentaire a une épaisseur constante H. On suppose pour simplifier qu’elle est homogène et qu’elle repose sur un demi-espace élastique.
Les coefficients de réflexion pour les potentiels de déplacement à la base de la couche sédimentaire sont RPP, RPS, RSS et RSP.
La figure montre que l’on enregistre des réflexions multiples qui ont fait un ou plusieurs aller-retour dans l’eau en plus du trajet descendant dans l’eau.
On considère un rayon entre la surface z = 0 et la profondeur z1. On note V1 = V(z1).
Soit maintenant un milieu où la vitesse diminue avec la profondeur selon V(z) = V1 – az . On a donc maintenant V1 = V(z = 0) et V0 = V(z1)
Soit maintenant un milieu où la vitesse varie selon la courbe de la figure 1.
La vitesse dans l’eau diminue de V1 = 1550 m/s à V0 = 1500 m/s sur une épaisseur d1 = 50 m .
Elle est ensuite constante V0 = 1500 m/s sur une épaisseur d0 = 50 m.
Sous l’eau, la vitesse dans les sédiments est V2 = 1600 m/s sur une épaisseur d2 = 100 m.
Pour les profondeurs supérieures à 200 m, la vitesse vaut V3 = 2000 m/s.
L’hodochrone correspondant à ce milieu pour une source ponctuelle en surface et des récepteurs en surface est représenté sur la figure 2.
Etablir les expressions analogues pour l’onde réfléchie et l’onde conique dues à l’interface située à la profondeur 200 m.
Qu’est ce qui change sur l’hodochrone de la figure 2 si la vitesse dans les sédiments augmente linéairement entre 100 et 200 m de profondeur de V2 = 1600 m/s à V'2 = 1700 m/s ?
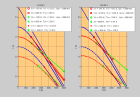
La figure 1 montre l’hodochrone T(X) pour l’onde directe et les ondes coniques dans la boue.
La figure 2 montre les valeurs des coefficients de réflexion et de transmission pour les potentiels de déplacement d’ondes planes de paramètre p à l’interface boue-roche.
Les valeurs sont obtenues en résolvant le système AR = B où R et B sont les vecteurs colonnes :
R = [Rφ , Tφ , Tψ]t ,
B = [-cosθ1/VP1 , -ρ1 , 0]t
et A est la matrice
Etablir les deux équations de continuité permettant d’obtenir la première et la troisième ligne ce système.
La figure 3 montre les vitesses de phase des ondes guidées dans la couche liquide pour le mode fondamental et les deux premiers harmoniques.
La figure 4 montre la valeur de detA lorsque p > 1/VP1 .
La simulation numérique de la propagation dans le puits cylindrique vertical permet de déterminer
la divergence et le rotationel du déplacement entre T = .2 et 1.6 ms.
A chaque intervalle de temps, le puits est à gauche et la roche à droite.
La simulation inclut toutes les ondes générées par les réflexions multiples dans la couche.
On voit apparaître en première arrivée sur le rotationel du déplacement à T = .4, .6 et .8 ms une onde conique dans la roche.
Stephen, R.A., F. Cardo-Casas, and C. H. Cheng , 1985, Finite-difference synthetic acoustic logs
On fait une première interprétation en utilisant seulement les deux droites qui apparaissent en première arrivée dans les intervalles 0
On utilise maintenant la réflexion qui arrive au temps T(X=0) = 1s.
On remarque une arrivée linéaire entre X1c, T1c et Xm, T1m.
On utilise maintenant la réflexion qui arrive au temps T(X=0) = 1.5 s.
Les ondes réfléchies par la surface et le fond de l’eau sont de fortes amplitudes. On observe en général sur les enregistrements en mer en plus des réflexions primaires ayant un trajet source-réflecteur-récepteur, des réflexions multiples ayant un trajet source-fond de l’eau-surface-réflecteur-récepteur.
L’hodochrone de la figure 2 est calculé avec le même modèle que celui de la figure 1, sauf la vitesse dans la couche 2 qui augmente linéairement avec la profondeur.
Déterminer le coefficient de réflexion R pour le déplacement des particules à la surface libre du demi-espace élastique pour une onde SH d’incidence η.
Déterminer les coefficients de réflexion R'φ et R'ψ pour les potentiels de déplacement des particules à la surface libre
du demi-espace élastique pour une onde incidente SV d’incidence η< ηc .
On suppose que l’onde SV incidente a une incidence η > ηc .
Ecrire l’expression du potentiel de déplacement de l’onde P évanescente.
Déterminer l’équation permettant de déterminer la vitesse de propagation VR de l’onde de Rayleigh se propageant le long de la surface libre du demi-espace.
II) On suppose maintenant que le demi-espace est recouvert d’une couche élastique d’épaisseur H , de vitesses VP1 et VS1 et de masse volumique ρ1.
Etablir, en fonction de ω , η1 , VS1 , H, la condition d’interférence constructive en z = -H entre l’onde SH transmise
directement en z = -H et celle qui a effectué une descente-montée supplémentaire dans la couche dans le cas où R1 est un nombre réel négatif.
On suppose maintenant que VS1 < VS et que l’onde SH dans le demi-espace est évanescente.
La vitesse de propagation horizontale de cette onde est VH telle que VS1 < VH < VS .
On suppose que l’onde se propage dans la direction x.
On suppose que l’onde harmonique de la figure 1 est une onde P et que la valeur maximum du déplacement ux(x,t) est Ux = 10-4 m.
La figure 2 montre le déplacement des particules ux(x,t) enregistré dans le même milieu de
vitesse de propagation V pour une onde de même période T se propageant dans le plan (x,z).
On suppose que l’onde harmonique de la figure 2 est une onde P et que la valeur maximum du déplacement ux(x,t) est Ux = 10-4 m.
On suppose que l’onde harmonique de la figure 2 est une onde S se propageant à la vitesse V et que la valeur maximum du déplacement ux(x,t) est Ux = 10-4 m.
II)
La figure montre les temps de trajet calculés pour un milieu comportant deux couches de vitesses constantes V1 et V2 et d’épaisseur H1 et H2 surmontant un demi-espace de vitesse constante V3.
La figure montre les temps de trajet calculés pour un milieu comportant une couche de vitesse constante V1 d’épaisseur H1, une couche d’épaisseur H2 où la vitesse augmente linéairement de V2 à V3 du sommet à la base de la couche, surmontant un demi-espace de vitesse constante V3.
Solution : osex05.m
I) Calcul des temps de trajet pour une source ponctuelle et des récepteurs placés dans les sédiments à une distance verticale d = 300 m au dessus de la
couche d’épaisseur H = 150 m. La distance horizontale source-récepteur est notée X.
II) Calcul des coefficients de réflexion R et transmission T pour le déplacement uy(x,z,t) d’une onde plane harmonique SH de paramètre p, à l’interface sédiment-basalte.
III) Calcul des coefficients de réflexion RH et transmission TH pour le déplacement uy(x,z,t) d’une onde plane harmonique SH de paramètre p et de pulsation w sur
une couche de basalte d’épaisseur H intercalée dans les sédiments.
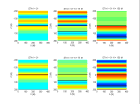
IV) Représentation du déplacement uy(x,z,t) résultant de la réflexion-transmission d’une onde plane harmonique SH sur une interface sédiment-basalte
et sur une couche de basalte d’épaisseur H pour une incidence η1 = 15 ° < ηc et une fréquence f = 10 Hz.
V) Représentation du déplacement uy(x,z,t) résultant de la réflexion-transmission d’une onde plane harmonique SH sur une interface sédiment-basalte
et sur une couche de basalte d’épaisseur H pour une incidence η1 = 30° > ηc et une fréquence f = 10 Hz.
On considère le modèle de vitesse stratifié suivant :
Etablir les équations permettant de calculer la géométrie des rayons sismiques issus d’une source ponctuelle et les temps de trajet des fronts d’onde se propageant dans un milieu où la vitesse de propagation est V(x, z).
Expliquer comment ces équations sont utilisées pratiquement pour tracer des rayons et calculer des temps de trajet à partir de la source.
Donner l’expression de l’angle d’incidence critique ηc et de la distance critique xc à partir de laquelle l’onde conique émerge en surface.
L’onde réfléchie sous incidence critique effectue des allers retours successifs dans la couche et engendre une onde conique à chaque rebond sur l’interface.
Déterminer les profondeurs des sources virtuelles correspondant aux ondes réfléchies une fois, deux fois, n fois sur l’interface.
II) On cherche maintenant à mettre en évidence la présence d’ondes guidées dans la couche.
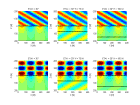
Pour ceci on effectue des filtrages qui font apparaître les ondes guidées à des fréquences de 5, 10, 15 et 20 Hz (figure).
On observe des oscillations périodiques dans des bandes distinctes à chaque fréquence.
A l’intérieur des bandes, la pente des ondes harmoniques augmente avec la fréquence entre 5 et 15 Hz.
A 20 Hz on observe deux pentes distinctes : une égale à celle observée à 5 Hz et une autre supérieure à celle observée à 15 Hz
(en fait cette dernière pente est difficile à observer à cause d’un intervalle entre traces trop grand).
Quelles sont les deux façons d’établir la relation de dispersion permettant de déterminer la vitesse de propagation VL(f)
d’une onde de Love dans une couche ?
Les figures sont empruntées à Kelly K.R., 1983, Numerical study of Love wave propagation.
L'article illustre aussi ce qui se passe si on introduit une variation latérale dans la couche.
Que représentent physiquement p et q ? Comment peut-on les mesurer ?
A) On suppose V = V(z)
B) On suppose maintenant V = V(x,z)
Bernasconi G. and G. Drufuca, 2001, 3-D traveltimes and amplitudes by gridded rays
proposent une méthode de tracé de rayons 3D basée sur ces équations.
II) Soit une source ponctuelle placée à l’origine et une interface entre deux milieux de vitesse V1 et V2>V1.
Soit un point M(xm, z = d) sur l’interface.
On suppose que l’angle d’incidence de l’onde directe en M est supérieur à l’angle d’incidence critique θc.
A) L’interface est plane et horizontale.
B) L’interface est plane avec un pendage α. Elle remonte pour les x croissants.
C) L’interface fait un angle en M : elle est horizontale pour 0 < x < xm et a un pendage α pour x>xm. On suppose α < θc .
La figure montre les rayons et fronts d’onde issus d’une source ponctuelle placée à une profondeur de 500 m au milieu
d’une zone à faible vitesse. La vitesse V(z) varie continûment selon le modèle :
Etablir les équations permettant de tracer les rayons et de calculer les temps de trajet pour ce type de modèle de vitesse.
II) Ondes SH guidées dans une couche
A - Réflexion-transmission sur une interface
Etablir l’expression des coefficients de réflexion R et transmission T pour le déplacement des particules uy(x,z,t)
d’une onde harmonique SH plane incidente à l’interface entre deux demi-espaces élastiques de vitesse VS1 et VS2
(VS1 < VS2) et densité ρ1 et ρ2 . On notera η1 et η2 les angles d’incidence mesurés par rapport à la verticale.
B - Onde guidée dans une plaque
Déterminer la valeur de kx pour une onde SH guidée correspondant au mode propre vertical fondamental de vibration
dans une plaque élastique à bord libre d’épaisseur H et de vitesse VS.
(Rappel : le mode propre fondamental d’une tige 1D de longueur H est défini par k = p/H)
C - Onde de Love guidée dans une couche à surface libre, d’épaisseur H et vitesse VS1 sur un demi-espace de vitesse VS2 > VS1 .
Expliquer pourquoi VS1 ≤ VL ≤ VS2 en considérant la réflexion totale d’ondes SH dans la couche.
D - Onde guidée SH dans une couche d’épaisseur H et vitesse VS1 en sandwich entre deux demi-espaces de vitesse VS2 > VS1 .
Ecrire la valeur de kz1 correspondant au mode propre vertical fondamental dans la couche en tenant compte des déphasages χ(p) à la réflexion totale sur les deux interfaces.
Etablir l'équation des ondes pour le déplacement des particules ux(x,t).
Donner l'expression de la vitesse de propagation de l'onde.
Ecrire le déplacement des particules comme la somme d'une onde f(x,t) qui se propage vers les x croissants et d'une onde
g(x,t) qui se propage vers les x décroissants, en supposant que f et g sont émises en x = 0 à t = 0 .
Même question en supposant que f est émise en x = -xs et g en x = +xs à t = 0 .
Dans ce dernier cas, on place en un point d'abscisse xr un capteur de déplacement qui enregistre
ux(xr,t) et un capteur de contrainte qui enregistre σxx(xr,t).
Les dérivées de f et g sont f' et g'. Ecrire l'expression de ux(xr,t) et σxx(xr,t)
dans les 3 cas suivants : xr>xs ; xr<-xs ; -xs<xr<xs .
Donner l'expression de la vitesse de déplacement des particules. Comparer avec l'expression de la contrainte.
En déduire que dans le cas où (-xs<xr<xs), on peut séparer l'onde qui se propage vers les x croissants de celle
qui se propage vers les x décroissants en additionnant ou soustrayant vitesse des particules et contrainte multipliée
par un facteur à déterminer.
Meunier, J. , F. Huguet and P. Meynier, 2001,
Reservoir monitoring using permanent sources and vertical receiver antennae: The Céré-la-Ronde case study
montrent comment les ondes montantes et descendantes enregistrées dans un forage sont séparées en combinant des enregistrements
de pression et de vitesse de déplacement.
II - La figure représente l'hodochrone T(X), sa pente et les rayons issus d'une source ponctuelle placée à l'origine
pour une propagation dans un milieu où la vitesse de propagation augmente linéairement avec la profondeur ( V(z) = V0+az ).
Rappeler et justifier la construction géométrique qui permet de tracer les rayons de paramètres p au compas.
Donner l'expression de la distance horizontale X(p) et du temps de propagation T(p) permettant de construire l'hodochrone
pour un récepteur situé sur la surface z = 0.
Rappeler les relations existant entre la pente de l'hodochrone et p, θ0 (incidence du rayon en z = 0),
V0 et Zm (profondeur maximum atteinte par le rayon). Déterminer les valeurs de V0 et a utilisées pour tracer la figure
à partir de la courbe donnant la pente de l'hodochrone.
Vérifier que les rayons dessinés s'obtiennent par la construction au compas.
Dessiner les fronts d'onde T(x,z) aux temps t = 1s et t = 2s . Ecrire l'équation iconale vérifiée par T(x,z).
Etablir les équations permettant de calculer la géométrie des rayons dans le cas où V(x,z).
III - La figure montre des enregistrements de ux(t), uy(t) et uz(t) pour un tremblement
de terre ainsi que les composantes longitudinales (radiales) et transverses du déplacement des particules obtenues par
rotation à partir des enregistrements précédents.
Etablir l'expression générale du mouvement des particules pour des ondes planes P et S et les caractéristiques de
leur polarisation.
Identifier les différentes ondes enregistrées.
Estimer l'angle et le plan d'incidence de l'onde à partir du mouvement des particules de l'onde P.
Compte tenu des valeurs de Vp et Vs dans la croûte, l'échelle des temps indiquée sur la figure représente-elle
le temps de propagation des ondes depuis la source ?
Montrer que le temps de propagation d'une onde conique entre une source ponctuelle S située à une distance d d'une
interface et des récepteurs situés à la même distance d de l'interface que la source S et à une distance horizontale X
de la source s'exprime comme la somme des temps de propagation correspondant à :
La figure montre les fronts d'onde à un temps t issus d'une source ponctuelle S
à une distance d d'une interface entre deux demi-espace élastiques de vitesses
VP2>VS2>VP1>VS1.
Les différents fronts sont générés à partir d'une onde P émise en S en prenant en compte les conversions P-S à
l'interface entre deux demi-espaces élastiques.
Donner l'expression des incidences critiques pour les transmissions P1-P2, P1-S2, S1-S2, S1-P2.
Identifier les différents fronts d'onde représentés sur la figure.
Dessiner les rayons représentant les trajets des différentes ondes coniques entre S et un récepteur situé à la distance d
de l'interface.
Déterminer le temps de propagation des différentes ondes coniques remontant depuis l'interface entre S et des récepteurs
situés à la distance d de l'interface et à des distances horizontales X de la source.
II. Réflexion-transmission d'une onde SH harmonique plane
La figure montre le déplacement des particules pour des ondes harmoniques SH générées à l'interface entre deux
demi-espaces par une onde incidente dans le demi-espace supérieur.
Vérifier que les ondes obéissent à la loi de Snell en mesurant :
Expliquer précisément ce que l'on observe sur chacune des figures.
Qu'observerait-on à un temps t = 0.25 s, sachant que f = 2 Hz et en supposant que l'image représente les ondes à t=0 ?
Déterminer les épaisseurs possibles pour une couche de vitesse V1 = 2000 m/s sur un demi-espace de vitesse
V2 = 2600 m/s dans laquelle se propage une onde de Love de vitesse de phase VL(f=2Hz) = 2538 m/s.
Donner l'ordre de grandeur des longueurs d'onde correspondantes pour une fréquence de 10Hz pour une roche
sédimentaire et une roche granitique.
En déduire le rapport entre les amplitudes maximums des déformations associées à chaque onde si l'on suppose
que l'amplitude maximum du déplacement des particules est la même pour les deux ondes.
Même question pour les contraintes. Donner leur ordre de grandeur pour une amplitude maximum du déplacement de 1 mm.
Déterminer la polarisation du déplacement des particules pour une onde plane P se propageant dans un milieu élastique
homogène.
Même question pour une onde plane S.
Qu'est-ce qu'une onde SV ? une onde SH ? Pourquoi distingue-t-on ces deux types d'onde ?
Déterminer l'expression du déplacement des particules pour une onde harmonique P sphérique se propageant à partir
de l'origine dans un milieu acoustique homogène d'incompressibilité K.
Soit une interface de pendage α entre une couche de vitesse V1 et un demi-espace de vitesse V2>V1.
Une source ponctuelle S est située sur la surface horizontale à une distance d de l'interface
(d est mesurée perpendiculairement à l'interface).
Un récepteur R est situé sur la surface à la distance horizontale X de la source S.
Le récepteur est situé du coté aval par rapport à la source.
Soit un milieu dans lequel la vitesse augmente linéairement avec la profondeur de V0 à V1 entre z=0 et z=d,
puis diminue de V1 à V0 entre z=d et z=2d (le gradient change de signe), puis augmente à nouveau à partir de z=2d
avec le même gradient qu'en surface.
Le rayon qui part de l'origine et qui a son point bas en z=d atteint la surface à une distance X de l'origine.
Donner les expressions suivantes dans un milieu de vitesse constante V :
Représenter la géométrie des rayons permettant de construire sans calcul, mais en respectant les vitesses apparentes
des ondes le long de l'axe Ox, les hodochrones t(x, z=0) donnant les temps de propagation observés en fonction de la
distance horizontale parcourue pour chacun des milieux de propagation acoustique suivants
(on dessinera pour chaque cas à la verticale l'une de l'autre une figure dans le plan (x,z) pour les rayons et
(x,t) pour les hodochrones, en respectant pour chaque rayon représenté la correspondance en x du point d'émergence
du rayon et du temps de parcours t(x) ) :
Montrer qu'une onde plane harmonique solution de l'équation des ondes peut s'écrire sous la forme :
Peiω(T(x,y,z)-t) et exprimer T(x,y,z) en fonction de V et de la direction de propagation e .
On considère que dans l'équation des ondes la vitesse de propagation V est fonction de (x,y,z).
On cherche une solution sous une forme analogue à celle d'une onde plane mais avec une amplitude P fonction de (x,y,z) :
p=P(x,y,z)eiω(T(x,y,z)-t)
Voici une simulation numérique
(Jensen F.B., Kuperman W.A., Porter M.B. and H. Schmidt, 1994, Computational ocean acoustics, AIP Press, pl.12)
de la propagation d'une onde émise par une source ponctuelle située à l'origine
(a est la situation au temps t=0.02 s, b à t=0.06 s, et c à t=0.12 s).
Déterminer la distance critique Xc
Calculer le temps de propagation de l’onde réfléchie pour le rayon se propageant verticalement (rappel : T = 2 ∫dz/V(z))
Dessiner l’hodochrone T(X)
Examen 2014
Soit une interface plane horizontale entre deux demi-espaces élastiques homogènes ayant des vitesses de propagation pour les ondes S : VS1 = 2000 m/s et VS2 = 2500 m/s.
L’angle d’incidence est l’angle entre la direction de propagation de l’onde et la verticale. ηc est l’angle d’incidence critique sur l’interface.
L’impédance (masse volumique x vitesse) du milieu 1 est I1 = ρ1VS1.
Le coefficient de réflexion pour le déplacement des particules d’une onde plane SH incidente avec un angle d’incidence η1 dans le milieu 1 est noté R.
Dans le cas où η1 < ηc , écrire R(I1, η1 , I2 , η2) où I2 est l’impédance du milieu 2 et η2 l’angle d’incidence de l’onde transmise dans le milieu 2.
Déterminer la valeur de l’impédance I2 puis de la masse volumique ρ2 sachant que la valeur mesurée de R(I1 = 4*106 kg/m2/s, η1 = 30°) = - 0.1.
Dans le cas où η1 > ηc , écrire R(p, I1, VS1 , I2 , VS2) où p est le paramètre de rai (inverse de la vitesse apparente horizontale des ondes).
Déterminer la valeur du déphasage χ à la réflexion lorsque l’angle d’incidence de l’onde SH dans le milieu 1 vaut η1 = 60°.
Ecrire la condition d’interférences constructives dans la couche pour des ondes SH planes harmoniques de pulsation ω = 2πf totalement réfléchies à la surface libre et sur l’interface
en fonction de ω, VS1 , H, η1 , χ.
Déterminer la fréquence f du mode fondamental de l’onde de Love guidée à la vitesse VL = 2309 m/s. (Rappel : VL est la vitesse apparente horizontale des ondes SH dans la couche).
φ(x,z,t) = Φexp(-kzPz ) exp(i(kxx-ωt) ) et ψy(x,z,t) = Ψexp(-kzSz ) exp(i(kxx-ωt) ).
Donner les expressions de kx, kzP et kzS en fonction de ω , VR, VP et VS
Enoncer, sans faire les calculs, les conditions aux limites sur la surface libre permettant de déterminer VR .
Dans quel intervalle VR / VS varie-t-il pour un demi-espace élastique homogène ?
Le rapport entre les amplitudes des potentiels des ondes évanescentes P et SV constituant l’onde de Rayleigh est : Φ/Ψ = iA(VR , VS)
Montrer qu’il existe un déphasage de π/2 entre les composantes ux et uz du déplacement des particules de l’onde de Rayleigh à la surface libre (z = 0)
Quelle est la conséquence de ce déphasage sur la trajectoire des particules en z = 0 ?
Déterminer l’expression de la vitesse de propagation d’une onde SH en fonction de l’angle d’incidence η, de la masse volumique ρ et des coefficients élastiques a et b.
Contrôle continu 2014
Soit une onde plane P se propageant dans une direction e dans un milieu élastique homogène.
Les composantes du vecteur unitaire e sont ex = cosα , ey = cosβ , ez = cosγ.
La vitesse de propagation est VP.
Soit u le déplacement des particules. Ecrire la relation entre la contrainte σxx , la déformation volumique divu et la déformation εxx
en fonction des paramètres de Lamé λ et μ du milieu.
Exprimer VP en fonction de λ et μ et de la masse volumique ρ.
Quelle est la valeur de VP pour l’eau ? Quel est l’intervalle de VP rencontré dans un bassin sédimentaire ?
Ecrire le potentiel φ(x,y,z,t) du déplacement des particules.
Montrer que la polarisation de l’onde est longitudinale (u et e sont colinéaires).
Donner l’expression de la vitesse apparente Vax de l’onde le long de l’axe Ox en fonction de α et VP.
Ecrire la relation entre les vitesses apparentes Vax , Vay , Vaz et VP sachant que e.e = 1.
Donner l’expression de Td(X) pour l’onde directe de vitesse V1.
Donner l’expression de l’angle critique θc1 à l’interface 1,2.
Donner l’expression de Tc1(X) pour l’onde conique de vitesse V2 en fonction de V1, V2, d1 et θc1.
Ecrire l’équation donnant X1 pour le point d’intersection entre Td(X) et Tc1(X).
Donner l’expression de l’angle critique θc2 à l’interface 2,3 et de l’angle d’incidence θ1 correspondant dans la couche 1.
Donner l’expression de Tc2(X) pour l’onde conique de vitesse V3 en fonction de V1, V2, V3, d1 , d2 , θ1 et θc2 .
Ecrire l’équation donnant X2 pour le point d’intersection entre Td(X) pour l’onde directe et Tc2(X).
Dessiner les hodochrones T(X) pour les ondes directes et coniques en respectant les pentes dans les deux cas suivants : a) X1
Dans ce dernier cas, quelle erreur fait-on en déterminant le modèle en utilisant uniquement les temps de première arrivée ?
Pour une source à la surface de la couche, les rayons sismiques dans la couche sont des arcs de cercle centrés en z = -V0/a et de rayon R = 1/(ap) où p est le paramètre du rayon sismique.
Dessiner l’hodochrone pour l’onde qui se propage dans la couche sans atteindre la profondeur d. Préciser sa pente en X = 0 et en Xmax, la distance horizontale maximum atteinte par cette onde.
Donner l’expression de Xmax en fonction de a, V0 et V1.
Dessiner l’hodochrone pour l’onde réfléchie à la profondeur d. Préciser sa pente en X = 0 et en Xmax.
Dessiner l’hodochrone pour l’onde conique se propageant sous l’interface à la vitesse constante V2.
Soit s l’abscisse curviligne le long d’un rayon. Donner l’expression de d(gradT)/ds et expliquer comment cette expression permet de tracer les rayons dans ce milieu.
Examen 2013
Contrôle continu 2013
Examen 2012
Contrôle continu 2012
Examen 2011
Contrôle continu 2011
Examen 2010
Contrôle continu 2010
Examen 2009
Contrôle continu 2009
L’hodochrone sur la partie inférieure de la figure montre les temps d’arrivée pour une source ponctuelle placée en x = 0 , z = 0
pour un milieu comportant une couche de vitesse V1 = 1000 m/s , d’épaisseur d constante, sur un demi-espace de vitesse V2 = 2000 m/s.
Les temps d’arrivée sont indiqués en millisecondes.
Il s’agit de dessiner les fronts d’onde à différents temps dans le plan (x,z) représenté sur la partie supérieure de la figure.
Déterminer l’épaisseur d de la couche à partir du temps de l’onde réfléchie en x = 0 et tracer l’interface z = d sur la figure.
Attention, le temps de l’onde réfléchie correspond au temps aller-retour dans la couche.
Indiquer sur la figure la position des différents fronts d’onde en z = 0 aux temps t1 = 600, t2 = 1300 et t3 = 2000 millisecondes
(indiqués par des lignes noires sur l’hodochrone).
Tracer les fronts d’onde directs dans la couche à ces 3 temps.
Tracer les fronts d’onde réfléchis dans la couche à ces 3 temps (vous pouvez utiliser la source virtuelle).
Déterminer la valeur de l’angle critique θc à l’interface.
Tracer les fronts d’onde coniques aux temps t2 et t3 en utilisant les positions des fronts d’onde conique en z = 0 et la valeur de θc .
En déduire la position des fronts d’onde transmis sur l’interface z = d aux temps t2 et t3.
Calculer les profondeurs atteintes par l’onde transmise aux temps t1 et t2 en x = 0 et tracer les points correspondant.
Déterminer la géométrie du rayon partant de la source sous l’incidence θ1 = 20° par rapport à la verticale : abscisse de l’intersection du rayon avec l’interface,
angle θ2 , position (x1 , z1) du front d’onde transmis au temps t1 le long du rayon, (x2 , z2) au temps t2 , (x3 , z3) au temps t3 .
Dessiner sur la figure les positions du front d’onde transmis aux temps t1 , t2 et t3 à partir des positions déterminées en x = 0,
le long du rayon θ1 = 20° et le long de l’interface.
Expliquer en quoi l’hodochrone serait différent si la vitesse V dans la couche, supposée à nouveau d’épaisseur d constante,
augmentait avec z selon la loi V(z) = V0+ az avec V0 = 1000 m/s et a = 1 /s.
Examen 2008
On étudie la propagation d’ondes planes harmoniques de type SH dans un milieu stratifié.
Le déplacement des particules est : uy(x,z,t) = Uexp(i(kxx+kzz-ωt)) où kx = ωp et p = sinη/V .
Le coefficient de réflexion sur une interface V0 / V est R = (I0- I)/( I0+ I) où I = ρVcosη.
Le coefficient de transmission est T.
Etablir l’expression du coefficient de réflexion Rh sur la couche en prenant en compte :
a) Une seule réflexion à l’intérieur de la couche
b) La série des réflexions successives à l’intérieur de la couche
Ecrire la condition d’interférence constructive dans la couche et donner la valeur maximum de Rh
Donner l’expression du déphasage χ(p) à la réflexion totale sur le demi-espace.
Ecrire la condition d’interférence constructive dans la couche en prenant en compte ce déphasage.
En déduire la relation de dispersion ω(p) où p = 1/VL pour :
a) le mode fondamental - b) le premier harmonique
Etablir la matrice Ai reliant les vecteurs colonne (Di+1 , Mi+1) et (Di , Mi) en exprimant successivement
Mi+1 et Di en fonction de Ri , hi , Vi , kzi , Di+1 , Mi .
Vérifier que pour une couche à l’intérieur d’un espace homogène, cette relation permet de retrouver l’expression de Rh obtenue en I).
Retrouver la condition d’interférence constructive pour une onde de Love dans une couche en écrivant les relations entre une onde descendante D
et une onde montante M vérifiant les conditions aux limites sur la surface libre et sur l’interface où il y a réflexion totale.
Etablir la relation de dispersion pour une onde de Love se propageant dans un milieu à 2 couches de vitesses V2 et V1 sur un demi-espace de vitesse V0
avec V2 < V1 < V0 . La couche de vitesse V2 est sous la surface libre, le coefficient de réflexion à l’interface V2 / V1 est R1 et il y a réflexion totale
à l’interface V1 / V0. Utiliser la matrice A1, la relations entre M1 et D1 sur l’interface V1 / V0 et la relation entre M2 et D2 à la surface libre.
Faire la somme et la différence des deux équations obtenues et montrer qu’on obtient :
I2tg(kz2h2)+I1tg(kz1h1+χ/2) = 0
Ecrire la relation de dispersion précédente en faisant apparaître la vitesse VL.
Examen 2007
On s’intéresse à des enregistrements faits par des capteur placés au fond de l’eau, sur l’interface eau-sédiment (représentés ci-dessous par de x).
Chaque capteur comporte 3 composantes enregistrant la variation de pression P dans l’eau et les vitesses de déplacement vx et vz des sédiments à l’interface.
La figure montre un enregistrement de P et vz à des capteurs placés au fond de l’eau, en ligne le long de l’axe x, pour une source S placée à la surface de l’eau.
L’offset représente le déport horizontal entre la source et le capteur. La propagation se fait dans le plan vertical (x,z).
La flèche indique une première arrivée de vitesse apparente supérieure à l’arrivée directe dans l’eau. De quelle onde s’agit-il ?
Dessiner le rayon correspondant à cette arrivée. Pourquoi est-elle difficilement discernable sur la composante vz ?
Peut-on mesurer précisément la vitesse de propagation sous l’eau avec cette arrivée avec l’intervalle d’offset enregistré ?
Etablir les équations permettant de calculer les coefficients de réflexion et transmission R, TP et TS pour les potentiels de déplacement dans le cas
d’une onde incidente plane harmonique descendante se propageant dans l’eau avec l’incidence θ0 .
Les équations peuvent se mettre sous la forme du système matriciel AR = B où R et B sont les vecteurs colonnes :
R = [R , TP , TS ]t , B = [cosθ0/V0 , ρ0 , 0]t.
Ecrire le rapport entre vz et P dans l’eau en z = 0 en fonction du coefficient de réflexion R(p).
Comment peut-on déterminer ρ ,VP et VS pour les sédiments à partir de la mesure de vz et P pour l’arrivée directe ?
Sur la figure, le cadre entourant l’arrivée directe indique la zone dans laquelle les valeurs de P sont prises pour le calcul de la question précédente.
A quel éventail de valeurs de p a-t-on accès à partir de ces valeurs?
Ecrire le rapport entre vx et vz dans les sédiments en z = 0 en fonction de TP et TS.
Comment peut-on déterminer ρ ,VP et VS pour les sédiments à partir de la mesure de vx et vz dans les sédiments en z = 0 ?
Etablir les équations permettant de calculer les coefficients de réflexion et transmission rPP, rPS, et tPP pour les potentiels de déplacement dans le cas
d’une onde incidente plane harmonique montante se propageant dans les sédiments avec l’incidence θ .
Etablir les équations permettant de calculer les coefficients de réflexion et transmission rSS, rSP, et tSP pour les potentiels de déplacement dans le cas
d’une onde incidente plane harmonique montante se propageant dans les sédiments avec l’incidence η .
En supposant toujours VS < V0 < VP et une source à la surface de l’eau, dessiner les rayons correspondant à un paramètre p donné pour les différentes ondes
enregistrées dans le cas où p < 1/VP et dans le cas p > 1/VP . On ignore les réflexions qui font des allers-retours multiples dans l’eau et les sédiments.
Ecrire les relations liant les potentiels de déplacement D et M des ondes planes harmoniques descendante et montante dans l’eau en z = 0 avec
les potentiels de déplacement DP , DS , MP et MS des ondes descendantes et montantes dans les sédiments en z = H.
Montrer qu’on peut obtenir M en fonction de D si l’on suppose qu’aucune onde montante ne vient du demi-espace.
Identifier le premier multiple de l’onde directe dans l’eau sur la figure.
Montrer qu’on peut obtenir l’expression des potentiels de déplacement de toutes les ondes ayant subi un aller-retour dans l’eau à partir du calcul de M
effectué précédemment en l’utilisant comme onde descendante incidente sur la couche sédimentaire après avoir effectué un aller-retour dans l’eau
d’épaisseur H0 et une réflexion à la surface de l’eau.
Contrôle continu 2007
Soit un milieu où la vitesse de propagation augmente avec la profondeur selon V(z) = V0 + az
Montrer que les rayons sismiques sont des cercles centrés sur la droite z = -V0/a .
Dans quel intervalle le paramètre p de ce rayon est-il compris (pour que le rayon atteigne la profondeur z1 ) ?
Exprimer la distance horizontale X(p) et le temps de trajet T(p) correspondant au trajet entre la surface et z1 (sans passer par le point bas du rayon).
Montrer que, par symétrie, les rayons entre la surface z = 0 et la profondeur z1 sont des cercles centrés sur la droite z = z1+V0/a .
En déduire que les expressions de X(p) et T(p) déterminées précédemment sont utilisables dans ce cas.
Pour une source ponctuelle située en z = 0, montrer qu’il existe une zone d’ombre et donner la valeur du paramètre p du rayon correspondant à la limite de la zone d’ombre.
Dessiner un rayon correspondant à l’onde réfléchie au fond de l’eau.
Etablir X(p) et T(p) pour l’onde réfléchie au fond de l’eau.
Déterminer la distance maximum Xm à laquelle cette onde est observable et le temps de trajet Tm correspondant (marqué par un carré sur la figure 2).
Quelle est la pente de l’hodochrone en ce point ?
Déterminer la distance Xc correspondant à la distance minimum à laquelle l’onde conique issue de l’interface eau-sédiment est observée et le temps de trajet Tc correspondant (marqué par un cercle sur la figure 2).
Donner l’expression T(X) pour cette onde conique.
Examen 2006
Une sonde comportant une source sismique et des récepteurs est placée dans un forage.
La sonde est dans la boue de forage (VP1 = 1800 m/s, ρ1 = 1200 kg/m3). Elle est placée à une distance d = 0.1 m de l’interface boue-roche.
La roche est un espace élastique homogène (VP2 = 4000 m/s, VS2 = 2300 m/s, ρ2 = 2300 kg/m3).
Les distances source-récepteur sont comprises entre X = 0 et 3m (longueur de la sonde).
Pour simplifier, on remplace le forage cylindrique par une couche plane horizontale liquide d’épaisseur 2d en sandwich entre deux demi-espaces élastiques.
La source et les récepteurs sont à la distance d des deux interfaces planes limitant la couche.
Etablir les équations donnant T(X) pour chacune de ces ondes.
Déterminer les distances Xc et les temps Tc à partir desquels les ondes coniques sont observées sur les récepteurs.
-cosθ1/VP1
-cosθ2/VP2
-p
ρ1
-ρ2(1-2p2VS22)
-2ρ2VS22pcosη2/VS2
0
2ρ2VS22pcosθ2/VP2
-ρ2(1-2p2VS22)
Montrer que Rφ s’écrit sous la forme (a-b)/(a+b) et déterminer a et b.
(Rappel : Rφ = detA’/detA où A’ est obtenue en remplaçant la première colonne de A par le vecteur colonne B)
Préciser les valeurs de p pour lesquelles Rφ = eiχ(p) et déterminer χ(p).
Etablir les relations de dispersion ω(p) pour chacune de ces ondes.
(Rappel : à chaque aller-retour dans la couche de l’onde plane réfléchie totalement sur les interfaces, la somme des déphasages dus au trajet vertical dans la couche
et aux réflexions totales est un multiple de 2π )
Calculer les fréquences de coupure ωc pour chacune de ces ondes et vérifier que vous obtenez la valeurs de la figure 3.
(Rappel : la fréquence de coupure est la fréquence minimum de la courbe de dispersion, obtenue pour la vitesse de propagation maximum de l’onde guidée ;
utiliser la figure 2 pour obtenir la valeur χ(p) correspondante)
Expliquer pourquoi cette courbe permet de déterminer la vitesse de propagation de l’onde guidée par l’interface lorsque toutes les ondes sont évanescentes.
Déterminer la vitesse de propagation de l’onde guidée le long de l’interface.
Déterminer la distance à l’interface d1 pour laquelle l’onde évanescente dans la boue a une amplitude réduite de 1/e par rapport à l’amplitude maximum à la fréquence f = 15000 Hz.
En utilisant l’hodochrone de la figure 1 et les résultats obtenus, indiquer la position des ondes suivantes aux temps suivants :
onde P transmise dans la roche et onde conique dans la boue à T = .6 ms
onde S transmise dans la roche à T = 1.2 ms
ondes guidées dans la boue à T = 1.4 ms
ondes évanescentes P et S dans la roche à T = 1.6 ms
Quelle peut-être son origine ? (Suggestion : avec quelle onde coïncide-t-elle sur l’interface ? )
Contrôle continu 2006
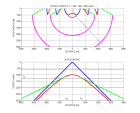
La figure 1 montre l’hodochrone calculé pour une expérience de sismique en mer faite avec un dispositif d’enregistrement d’une longueur de 6000 m.
On suppose que les interfaces sont planes et horizontales.
En déduire l’épaisseur d de la couche d’eau.
Vérifier qu’il s’agit de la réflexion au fond de l’eau, c’est à dire qu’elle correspond à la vitesse V1 (utiliser T(X=0) et les valeurs X1c, T1c données sur la figure).
En déduire l’épaisseur d1 de la couche d’eau.
Utiliser cette droite et les deux droites observées en première arrivée pour déterminer V1, V2, V3 et les épaisseurs d1 et d2.
Expliquer pourquoi la profondeur d était inexacte.
Vérifier que ce temps est compatible avec le modèle précédent.
Etablir les équations paramétriques permettant de calculer X(p) et T(p) pour cette réflexion.
Vérifier que ces équations donnent X2c et T2c pour la valeur de paramètre qui convient.
Préciser les bornes de l’intervalle de paramètres correspondant à cette réflexion.
Etablir l’équation donnant T(X) pour la réflexion multiple réfléchie deux fois au fond de l’eau. Vérifier qu’elle correspond à la réflexion qui arrive au temps T(X=0) = 2 s et que X11c et T11c correspondent aux valeurs attendues.
Etablir les équations paramétriques permettant de calculer X(p) et T(p) pour la réflexion multiple réfléchie une fois au fond de l’eau et une fois à la base de la couche 2. Vérifier qu’elle correspond à la réflexion qui arrive au temps T(X=0) = 2.5 s et que X12c et T12c correspondent aux valeurs attendues.
Décrire ce qui change par rapport à la figure 1.
Déterminer la vitesse dans la couche 2.
Calculer X1m, T1m, X2c, T2c, et T(X=0) pour la réflexion à la base de la couche 2.
osex06.m
Examen 2005
I) On considère un demi-espace élastique isotrope (x , z > 0) de vitesses VP et VS et masse volumique ρ.
On s’intéresse aux composantes du déplacement des particules ux , uy, uz enregistrées sur la surface libre z = 0 lorsqu’une onde plane harmonique S se propageant vers le haut est incidente sur la surface libre.
Les angles d’incidence des rayons (θ pour une onde P, η pour une onde S) sont mesurés par rapport à la verticale (θ = 0 pour une propagation verticale).
On note p le paramètre des rayons et ηc l’incidence critique correspondant au rapport VS/VP .
En déduire le déplacement des particules à la surface libre du demi-espace élastique si l’amplitude du déplacement des particules de l’onde SH incidente vaut 1.
Déterminer, en fonction de R'φ , R'ψ , VP , VS , p , cosθ , cosη, les composantes du
déplacement à la surface libre du demi-espace élastique si l’amplitude du potentiel de déplacement de l’onde SV incidente vaut 1.
Montrer que R'ψ = eiχ' et donner l’expression de χ' en fonction de VP , VS , p .
Montrer que R'φ = | R'φ |eiχ'/2 .
Déterminer, en fonction de |R'φ| , &chi'; , VP , VS , p , les composantes du déplacement des particules
à la surface libre du demi-espace élastique si l’amplitude du potentiel de déplacement de l’onde SV incidente vaut 1.
Ecrire les composantes du déplacement des particules de l’onde de Rayleigh à la surface libre du demi-espace élastique si l’amplitude du potentiel de
déplacement de l’onde SV évanescente vaut 1.
On suppose qu’une onde plane harmonique SH se propageant vers le haut dans le demi-espace est incidente à l’interface z = 0 avec un angle d’incidence η.
Elle est transmise dans la couche avec l’incidence η1.
Le coefficient de réflexion pour le déplacement des particules au passage de la couche dans le demi-espace est R1.
Etablir la même condition dans le cas où R1 est un nombre réel positif.
On suppose que l’amplitude du déplacement de l’onde SH transmise directement dans la couche vaut 1.
Etablir celle du déplacement sur la surface libre en z = -H dans le cas où la condition d’interférence constructive est réalisée et en prenant en compte
l’onde transmise directement et celle qui a effectué une descente-montée supplémentaire dans la couche.
Même question en prenant en compte la série des réflexions successives dans la couche.
Montrer que R1 = eiχ1 et donner l’expression de χ1 en fonction
de ρ1 , ρ , VS1 , VS , VH .
Ecrire la condition d’interférence constructive en z = -H pour le déplacement des particules des ondes SH dans la couche.
En déduire les fréquences des ondes de Love se propageant dans la couche à la vitesse VH.
Contrôle continu 2005
I)
La figure 1 montre le déplacement des particules ux(x,t) pour une onde harmonique aux temps t = 0, 0.1, 0.2, 0.3, 0.4, 0.5 s.
Déterminer la longueur d’onde λ , la période T , la vitesse de propagation V
Quel est le sens de propagation de l’onde (vers les x croissants ou décroissants) ?
Dessiner le déplacement ux(x,t) enregistré par un capteur placé en x = 500 m en indiquant précisément les valeurs de temps pour lesquelles le déplacement est nul.
Dessiner la droite représentant le temps d’arrivée pour une onde issue de x = 500 m au temps t = 0.
Déterminer la valeur maximum de la vitesse de déplacement et de l’accélération des particules.
Déterminer la valeur maximum de la déformation εxx.
On suppose que la densité ρ = 2500 kg/m3 , déterminer la valeur maximum de la contrainte σxx
Déterminer l’angle d’incidence θ de l’onde mesuré par rapport à la verticale
Déterminer la valeur maximum du déplacement uz(x,t) qui serait enregistrée.
De quel type d’onde S s’agit-il ?
Déterminer la valeur maximum du déplacement uz(x,t) qui serait enregistrée.
Etablir les équations donnant les temps de trajet des différentes ondes en fonction de la distance horizontale X entre la source et le récepteur
Déterminer V1, V2, V3, H1 et H2 . Les coordonnées des points entourés d’un cercle sont (X1 = 850 m, T1 = 0.766 s) et (X2 = 1327 m, T2 = 1.248 s)
Etablir les équations donnant la distance horizontale parcourue et le temps de trajet de l’onde qui se propage dans les couches 1 et 2 en fonction du paramètre p du rayon
Dessiner tous les rayons correspondant aux valeurs de paramètre p1, p2, p3, p4, p5 tels que : 1/V1>p1>1/V2 , p2 = 1/V2 , 1/V2>p3>1/V3 , p4 = 1/V3 , 1/V3>p5
Expliquer les caractéristiques de la figure, en particulier aux point entourés d’un cercle.
Examen 2004
On s’intéresse à la propagation d’ondes SH dans un milieu comportant une couche de basalte d’épaisseur H intercalée dans des sédiments.
Les vitesses de propagation des ondes S sont V1 = 1200 m/s pour les sédiments, V2 = 3000 m/s pour le basalte.
Les densités sont ρ1 = 2000 kg/m3 et ρ2 = 2700 kg/m3.
Calculer T(X) pour l’onde directe et pour les ondes réfléchie et conique générées à l’interface sédiment-basalte.
Déterminer la distance critique Xc d’enregistrement de l’onde conique.
Calculer T(p) et X(p) pour l’onde réfléchie à la base de la couche de basalte (p est le paramètre du rayon).
Calculer T(p) et X(p) pour l’onde réfléchie ayant effectué deux allers-retours dans la couche.
Pour un récepteur situé à une distance X > Xc, ces ondes arrivent avec des vitesses apparentes horizontales différentes.
En s’appuyant sur la géométrie des rayons correspondant, classer ces ondes en fonction de leur vitesse apparente horizontale, de la plus lente à la plus rapide.
Dessiner l’hodochrone obtenu en respectant les pentes.
Déterminer les coefficients R et T en fonction de p, des vitesses et des impédances I1 = ρ1V1, I2 = ρ2V2.
Déterminer l’angle d’incidence η1 tel que R = 0.
Déterminer la valeur du déphasage χ(p) à la réflexion pour des incidences η1 > ηc.
Donner la valeur du déphasage à la transmission en fonction de χ(p)
Vérifier que les valeurs obtenues pour R(η1 = 0), η1(R = 0) , χ(η1 = 30°) sont identiques à celles de la figure.
Calculer le coefficient de réflexion R1 sur la couche en prenant en compte un seul aller-retour dans la couche. Exprimer R1 en fonction de R , H et kz, le nombre d’onde vertical dans la couche de basalte.
Pour calculer les coefficients RH et TH en tenant compte de tous les allers-retours dans la couche, on utilise les relations entre ondes descendantes et
montantes d1 et M1 en z = 0 au dessus de l’interface sédiment-basalte et d2 et M2 en z = H au dessus de l’interface basalte-sédiment :
La figure représente les coefficients obtenus pour une fréquence de 10 Hz pour des épaisseurs H = 75 m et H = 150 m.
Expliquer à quoi sont dues les différences entre les valeurs obtenues pour ces deux épaisseurs de la couche.
Comparer la valeur R1(η1 = 0) avec celle de RH(η1 = 0) dans le cas où H = 75 m. Pourquoi l’écart est-il important ?
Quelle différence y-a-t-il entre les figures du haut et celles du bas. Sur quelles figures observe-t-on :
Calculer la profondeur caractéristique de décroissance de l’onde évanescente dans le basalte (amplitude réduite d’un facteur 1/e).
Expliquer pourquoi on observe une onde transmise dans les sédiments sous la couche quand H = 75 m.
Dans quelle épaisseur de sédiments au dessus d’une interface sédiment-basalte peut-on avoir propagation d’une onde de Love de fréquence 10 Hz et
de vitesse de propagation 2400 m/s.
Etablir la relation de dispersion pour une onde de Love et utiliser la valeur de déphasage χ(η1 = 30°) pour retrouver ce résultat.
 -
-
 -
-
 -
-
Contrôle continu 2004
Un enregistrement sismique montre une valeur maximum de l’accélération a = 8 m/s2 et une valeur maximum de la vitesse de déplacement b = 0.64 m/s.
En supposant que ces valeurs correspondent à une onde plane harmonique de fréquence f, déterminer f puis la valeur maximum U du déplacement. Dans quel cas enregistre-t-on de telles valeurs ?
On enregistre les trois composantes ux, uy et uz du déplacement. Les valeurs ci-dessus sont observées sur la composante uy , les deux autres composantes étant nulles.
En supposant que l’angle d’incidence par rapport à la verticale est différent de 90°, de quel type d’onde s’agit-il ? Qu’en est-il si la direction de propagation est horizontale ?
En supposant que la vitesse de propagation est connue, comment peut-on déterminer l’angle d’incidence avec des enregistrements faits en plusieurs positions voisines en surface ?
Pour quels types d’onde peut-on déterminer l’angle d’incidence avec un enregistrement trois composantes fait en une seule position ? Comment ?
Déterminer la valeur maximum S de contrainte correspondant aux valeurs a et b ci-dessus en utilisant des valeurs de densité et de vitesses de propagation d’une roche granitique pour les différents type d’onde possibles
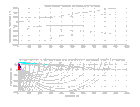
Déterminer les trajets et les temps de propagation des différentes ondes et dessiner l’hodochrone T(X) obtenu pour une expérience de sismique marine réalisée sur ce modèle dans les deux cas suivants :
Examen 2003
I) La figure montre le résultat de la modélisation numérique de la propagation d’ondes SH dans un modèle comprenant une couche surmontant un demi-espace.
Une source ponctuelle est placée en surface. La couche a une épaisseur d et une vitesse V1.
Le demi-espace a une vitesse V2 > V1.
L’enregistrement est fait en surface sur une distance horizontale x (0 à 3 km) très grande devant d (50 m) pendant 2.5 secondes.
On va chercher à comprendre comment une seule couche peut générer toutes ces
réverbérations
par réflexions successives sur l’interface et sur la surface libre
(on a parfois des enregistrements réels similaires lorsqu’il y a un fort contraste de vitesse).
Etablir l’équation donnant le temps de propagation tc de l’onde conique observée en première arrivée à une distance x > xc.
Dessiner les fronts d’onde incident, réfléchi, conique et transmis correspondant à un temps tel que l’onde conique passe en surface à une distance x grande devant xc.
Etablir l’équation donnant le temps de propagation tc1 de l’onde conique comportant un aller-retour supplémentaire dans la couche.
Etablir l’équation donnant le temps de propagation tcn de l’onde conique comportant n aller-retours supplémentaires dans la couche.
En déduire la périodicité avec laquelle les ondes coniques successives arrivent à un récepteur situé à une distance de la source très grande devant d.
Indiquer où ces ondes sont observées sur la figure.
Etablir l’équation donnant à une distance x le temps d’arrivée trn des ondes réfléchies n fois sur l’interface.
Sur la figure, la limite entre les zones de faible et de forte amplitude est une droite passant par l’origine.
Elle correspond à des arrivées de réflexions sous incidence critique effectuant des allers-retours multiples dans la couche.
Expliquer pourquoi on observe ce changement d’amplitude de part et d’autre de cette droite et déterminer la pente de cette droite.
Dessiner les fronts d’onde incident, réfléchis, coniques et transmis correspondant à un temps de propagation tels que plusieurs
ondes coniques soient observées en première arrivée en tenant compte des réflexions multiples et en respectant les tangences e
ntre les fronts d’onde réfléchis et les fronts d’onde coniques associés.
Etablir cette relation avec la méthode de votre choix.
Sur la base de ce que vous observez sur la figure, dessiner la courbe de dispersion VL(f) du mode fondamental et
du premier harmonique de l’onde de Love dans la couche.
Contrôle continu 2003
I) Un front d’onde sismique T(x,z) passe au point M(x,z) au temps t et au point M’(x+dx,z+dz) au temps t+dt.
M et M’ appartiennent au même rayon sismique d’incidence θ en M, θ+dθ en M’.
On note p et q les composantes de gradT . s est l’abscisse curviligne le long du rayon.
Expliquer pourquoi p est constant le long d’un rayon.
Etablir l’équation iconale reliant p, q et V.
Etablir les équations donnant dx/dz et dt/dz en fonction de q et V, puis de p et V.
Etablir l’équation donnant dq/ds en fonction de V et dV/dz. En déduire dq/dz.
Calculer dθ/dz en fonction de p, V, dV/dz de deux manières différentes : à partir de dp/dz, puis à partir de dq/dz.
Pourquoi p n’est-il plus constant le long d’un rayon ?
Exprimer dx/dz et dt/dz en fonction de p, q et V.
Exprimer dp/dz et dq/dz en fonction de q, V et des composantes de grad(1/V).
Proposer un algorithme permettant de tracer un rayon pas par pas selon la profondeur (c’est à dire par intervalle dz successifs).
Déterminer l’abscisse xc du point où l’onde conique issue de M arrive à la surface.
Déterminer les temps d’arrivée tm de l’onde transmise en M et tc de l’onde conique issue de M en surface.
Déterminer l’abscisse x’c du point où l’onde conique issue de M arrive à la surface.
Déterminer le temps de trajet t’c de l’onde conique entre le point M et la surface.
Dessiner les rayons correspondant aux ondes coniques montantes issues de M.
Dans quel intervalle le long de x observe-t-on deux arrivées coniques successives ?
En utilisant les rayons précédents, dessiner un front d’onde conique issu de la partie horizontale de l’interface et un front d’onde conique issu de la partie pentée.
Déterminer la différence de temps d’arrivée entre ces deux arrivées en x’c (utiliser la vitesse apparente horizontale).
Dessiner l’hodochrone des ondes coniques en respectant les pentes.
Que se passe-t-il si l’interface redevient horizontale en un point M’ tel que x’m>xm ?
Examen 2002
I) Rayons et fronts d’onde issus d’une source ponctuelle placée dans une zone à faible vitesse.
0 ≤ z ≤ 250 m : V(z) = 1000 + az avec a = 1 /s ; 250 ≤ z ≤ 500 m : V(z) = 1250 - a(z-250) ; z > 500 m : V(z) = 1000 + a(z-500)
Expliquer le comportement des différents faisceaux de rayons suivant l’angle d’incidence des rayons à la source.
Calculer le temps de trajet vertical T0 entre la source et la surface.
Dessiner l’hodochrone pour des récepteurs placés en z = 0 en utilisant la valeur de T0 et les valeurs de temps de propagation et d’angle d’incidence des rayons lues sur la figure.
En déduire les valeurs de R pour η1 = 0 , 30° , 60° pour une réflexion sur :
a) une surface libre, b) une interface solide-liquide, c) une interface entre deux couches sédimentaires
(choisir des valeurs réalistes de VS1 , VS2 , ρ1 et ρ2 )
Déterminer le déphasage χ(p) qui se produit à la réflexion totale lorsque η1 ≥ ηc .
Dans quel intervalle χ(p) varie-t-il lorsque 90° ≥ η1 ≥ ηc ?
En déduire la vitesse horizontale de propagation VG de l’onde guidée dans la couche en fonction de la pulsation ω , VS et H.
Expliquer pourquoi VG ≥ VS .
Ecrire la valeur de kz1 correspondant au mode propre vertical fondamental dans la couche en tenant compte du déphasage χ(p) à la réflexion totale sur l’interface.
En déduire ω(p) en fonction de χ(p) , VS1, et H.
Expliquer comment obtenir le graphe de la relation de dispersion VL(ω) du mode fondamental de l’onde de Love à partir de cette relation.
Comment obtient-t-on les relations de dispersion pour les différentes harmoniques ?
En déduire ω(p) en fonction de χ(p) , VS1, et H.
Contrôle continu 2002
I - On considère la propagation 1D d'ondes longitudinales le long d'une tige élastique de module d'Young E et masse volumique ρ.
Examen 2001
I . Ondes coniques élastiques
la propagation sur la distance horizontale X à la vitesse apparente horizontale de l'onde
la propagation sur une distance verticale aller-retour 2d à la vitesse apparente verticale de l'onde.
les angles d'incidence
les longueurs d'onde
Contrôle continu 2001
Déterminer le rapport entre les longueurs d'onde d'une onde P et d'une onde S sinusoïdales de même fréquence
se propageant dans une tige élastique homogène (propagation en 1D) en fonction du coefficient de Poisson ν ,
sachant que le module d'Young E et le coefficient de Lamé μ sont reliés par E=2μ(1+ν).
Déterminer les vitesses apparentes horizontales des différentes ondes reçues en R
Examen 2000
Soit un demi-espace (x, z≥0) élastique homogène de vitesses VP et VS.
L'angle entre la direction de propagation d'une onde et la verticale est noté θ pour une onde P, η pour une onde S.
Une onde plane harmonique de type SV se propageant vers le haut est incidente sur la surface libre z=0.
La figure (Aki K. & Richards P.G., 1980, Quantitative seismology, Freeman, p.159)
représente l'amplitude et la phase des coefficients de réflexion en fonction de la lenteur p
(inverse de la vitesse apparente horizontale des ondes) de l'onde SV incidente.
Contrôle continu 2000
Soit une source ponctuelle placée à l'origine et des récepteurs placés en ligne sur un même axe Ox à la surface z=0.
On considère des propagations dans le plan (x,z).
Examen 1999
Etablir l'équation des ondes dans le cas acoustique pour un milieu homogène et donner l'expression de la vitesse de
propagation V. Dans quelles parties de la Terre cette équation s'applique-t-elle? Avec quelles valeurs de V?
Etablir les équations permettant de déterminer la trajectoire des rayons dans un milieu où la vitesse de propagation V
est fonction de (x,y,z).
Contrôle continu 1999
On considère la propagation d'un front d'onde plan dans un milieu homogène.
La vitesse de propagation est V=1 km/s. On dispose un capteur tous les 200 m le long des axes Ox et Oy dans le plan z=0.
On considère maintenant que le demi-espace z<0 est homogène avec une vitesse V1=1 km/s et le demi-espace z>0 est
homogène avec une vitesse V2=1.4 km/s. On suppose que les capteurs sont placés à l'interface z=0 entre les deux milieux.
On considère maintenant la propagation d'un front d'onde sphérique issu d'une source ponctuelle S placée en (0, 0, -d)
dans un milieu homogène dont la vitesse de propagation est V=1 km/s.
On suppose à nouveau que le demi-espace z<0 est homogène avec une vitesse V1=1 km/s et le demi-espace z>0 est homogène
avec une vitesse V2=1.4 km/s. La source ponctuelle S est toujours placée en (0, 0, -d) dans le milieu 1.